新規記事の投稿を行うことで、非表示にすることが可能です。
2020年06月26日
大人のさび落とし 009 ベクトルと図形
01
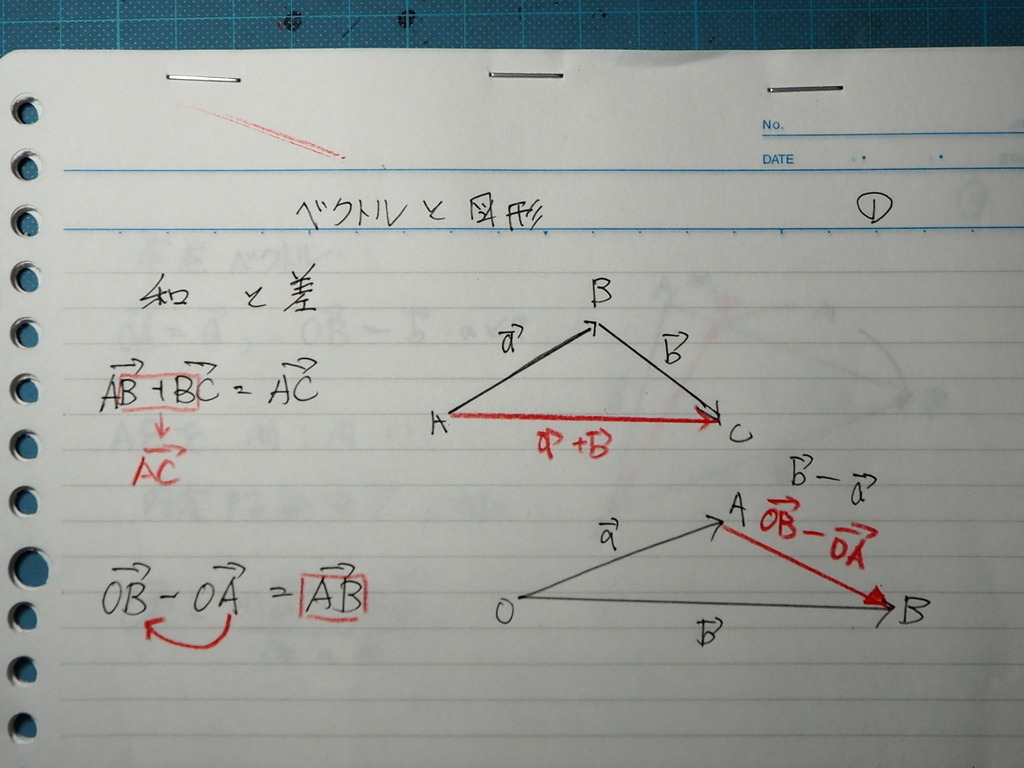
図形とベクトル
計算の 形
和 は
ひっつ目のベクトルの 終点から
次の ベクトルを 書く
かんじに
差 は
始点の おなじ 二つのベクトルの
先に 橋 を渡す感じで
方向は 差の式の
後ろから 前の様に
02
ベクトルの 大きさは
√(x成分の二乗 + y成分の二乗 )
ふつうの ベクトル 位置ベクトル のとき
成分を 引き算して
ベクトルを 求めたときも
その 成分に関して
√(x成分の二乗 + y成分の二乗 )

03
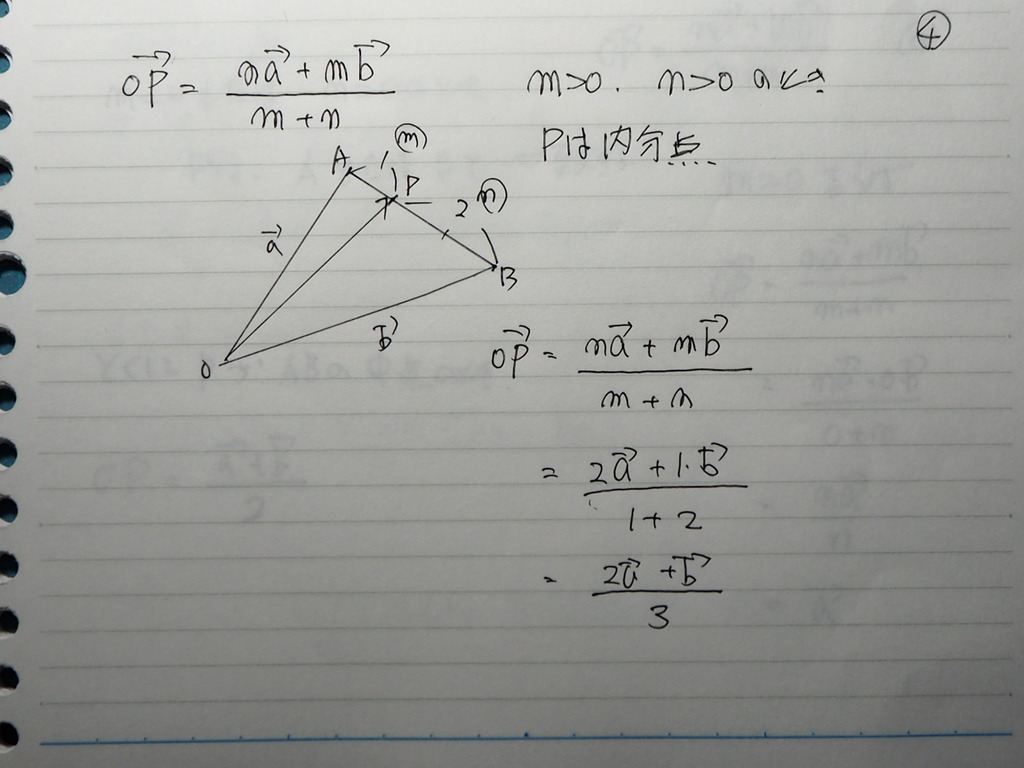
分点ベクトル
公式は これです

04
m>0 、n>0 の時は
内分点
分母は m+n
分子は それぞれの ベクトルに
遠い方 を 掛ける
m、n が 異符号の時
どっちかが マイナスになるときは
マイナス側が
AB の 外に来て
外分になる

06
m、または n、が =0の時は
分点は A または B に 一致する
OPが 中点の時は
2分の a+b

07
三角形 ABC で 重心を Gとすると
点O を それ以外の どこかにとって
位置ベクトルで表すとき
OGベクトルは 1/3( a+b+c)

08
平行の 条件は
0でない 実数倍で 表現できること

09
垂直条件
ベクトルは 成分で書かれてますが
垂直を 判別するのは 成分の
計算で

10
共線条件
3点が 一直線上にあるとき
始点を 合わせて
実数倍 表示ができること

11
実数倍が 負になるときは
始点を 合わせると
3 点 A,B,C があるとき
Aにたいして B、 C は
反対側 どうしになる

12
共線条件
位置ベクトルを 使って
直線 L、M の 交点 P
直線 M、N の 交点 Q
の 位置ベクトル
OP = OQ
を 示す

13
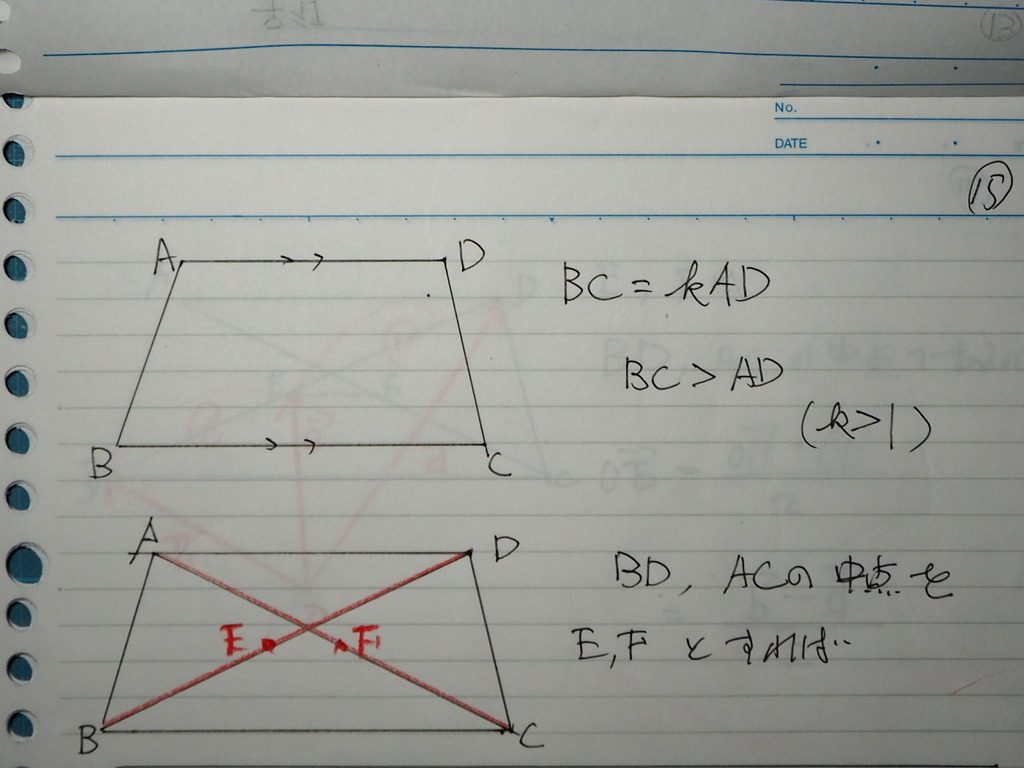
これらを 踏まえまして
問題
ある 台形 ABCD があって
( 条件があります
BC 平行 AD
BC > AD )
対角線の 中点を E、F
とすれば
次のことが 成り立つことを
証明しなさい
という問題

14
まず 平行条件
平行なので
始点が 一緒では ないですが
実数倍表示ができる
さらに
条件から
実数倍の K は
K > 1
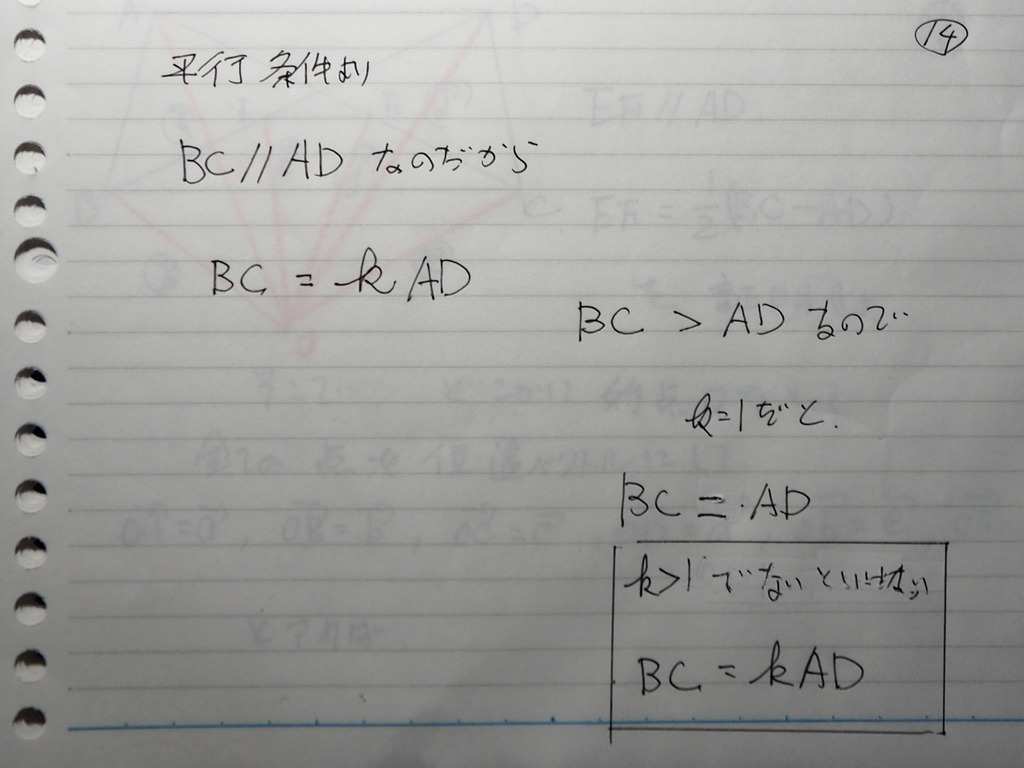
15
BD, ACの 中点を E,Fとするので
16
この時に
EF 平行 AD
EF = 1/2 ( BC - AD )
を 証明せよ
そこで
これらの 外に 点O を とって
位置ベクトルで
考えると
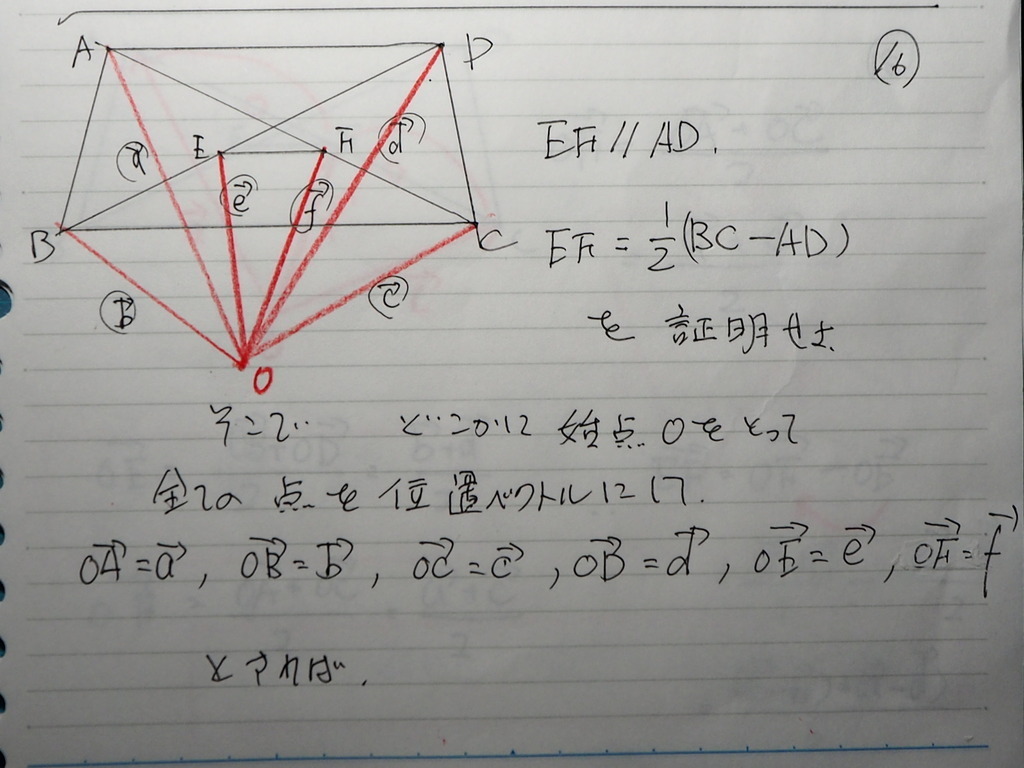
17
E,Fは それぞれ
BD、AC の 中点であるから
中点の 分点ベクトルで
OE ベクトル
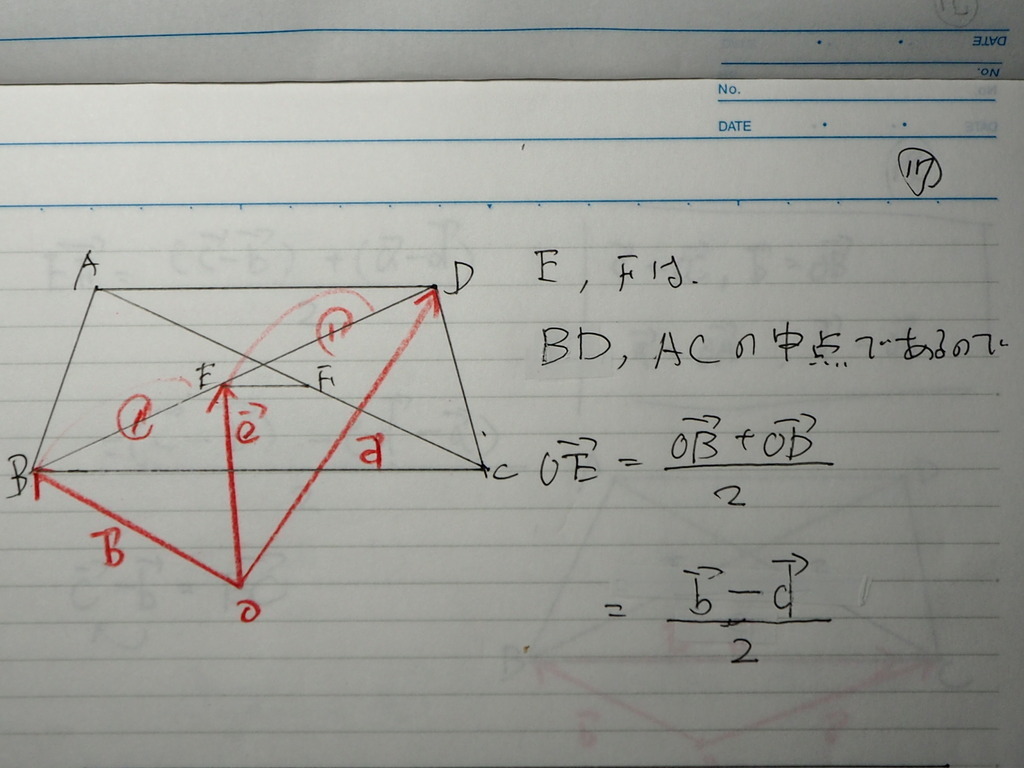
18
同じく
中点の 分点ベクトルで
OF
で EF ベクトルは
OF-OE
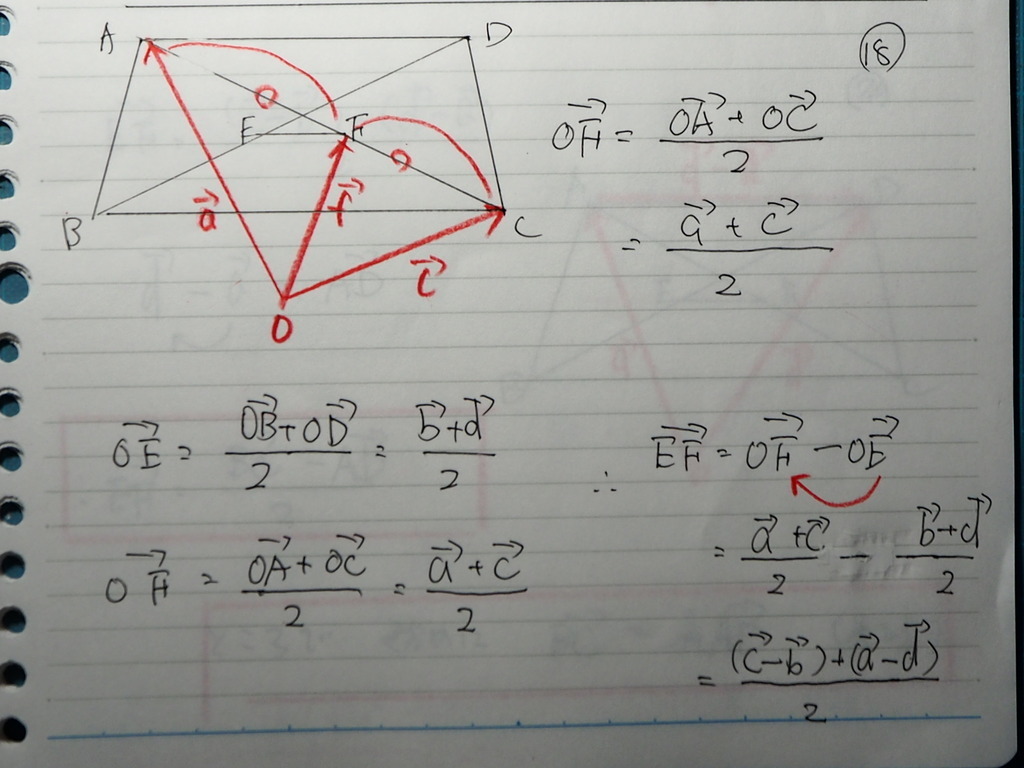
19
EF ベクトルの 分点ベクトル表示で
分子の 左かっこは
BCベクトル

20
EF ベクトルの 分点ベクトル表示で
分子の 右かっこは
ADベクトル
出てきた式に
始めの 平行条件を代入したら
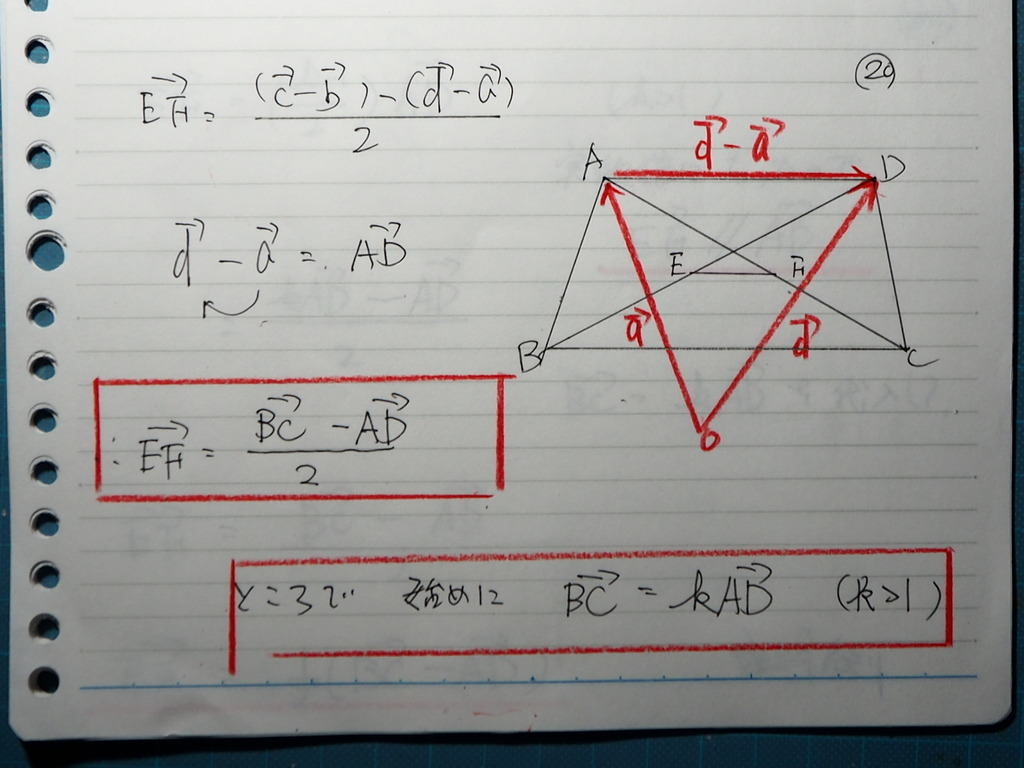
21
すでに ここで 答えが 出てるんですが
先に 平行であることを
言いたいので
式変形して

22
EFと ADが
実数倍表示が できたので
EF 平行 AD
そして
少し 前に戻る感じで
BC=K AD を 代入して
EF=1/2(BC-AD)

23
次は
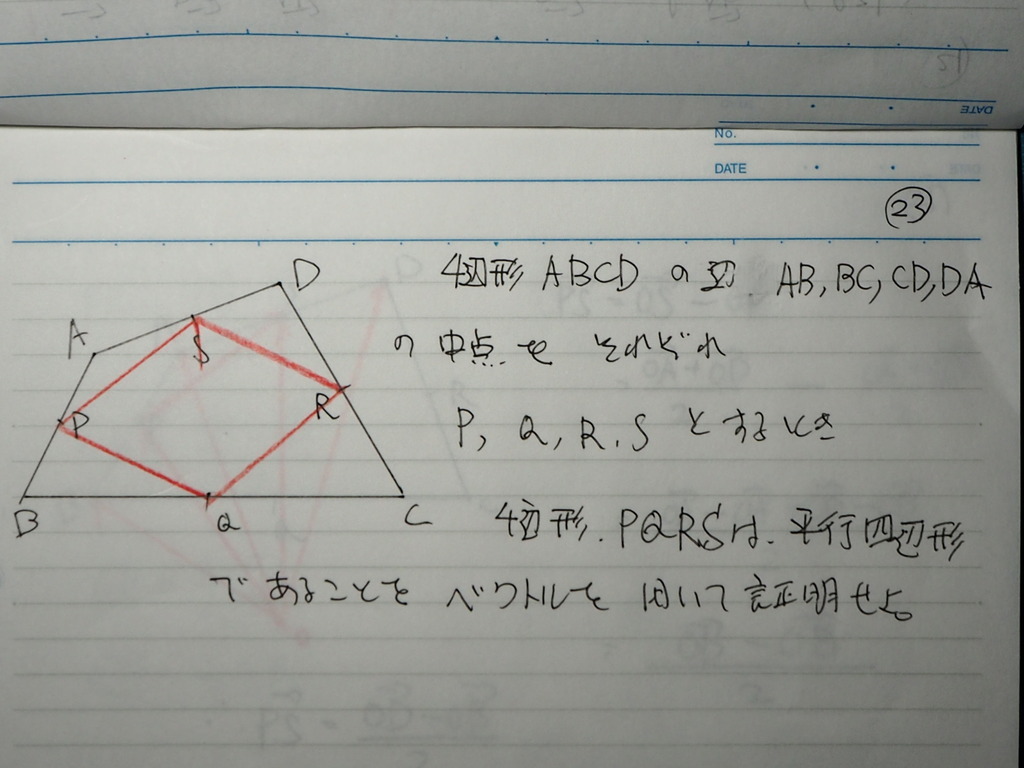
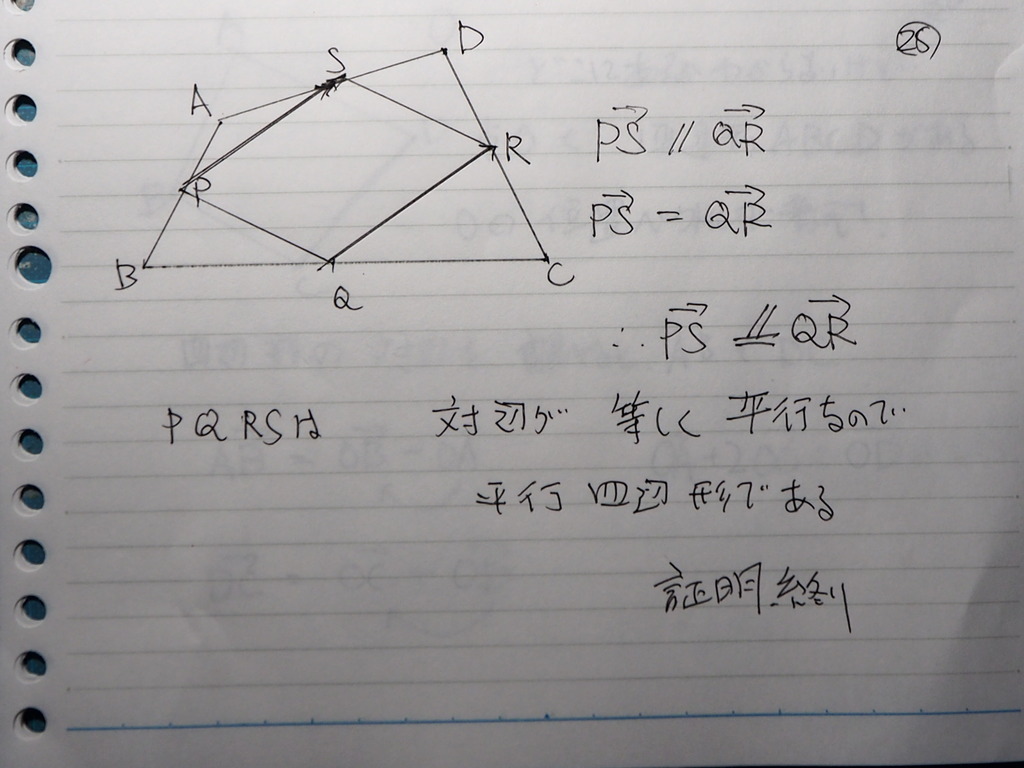
4辺形 ABCD が あるんだけども
それぞれ AB,BC,CD,DA の 中点を
P,Q,R,S とすると
4辺形PQRSは 平行四辺形 であることを
証明しなさい と言う 問題
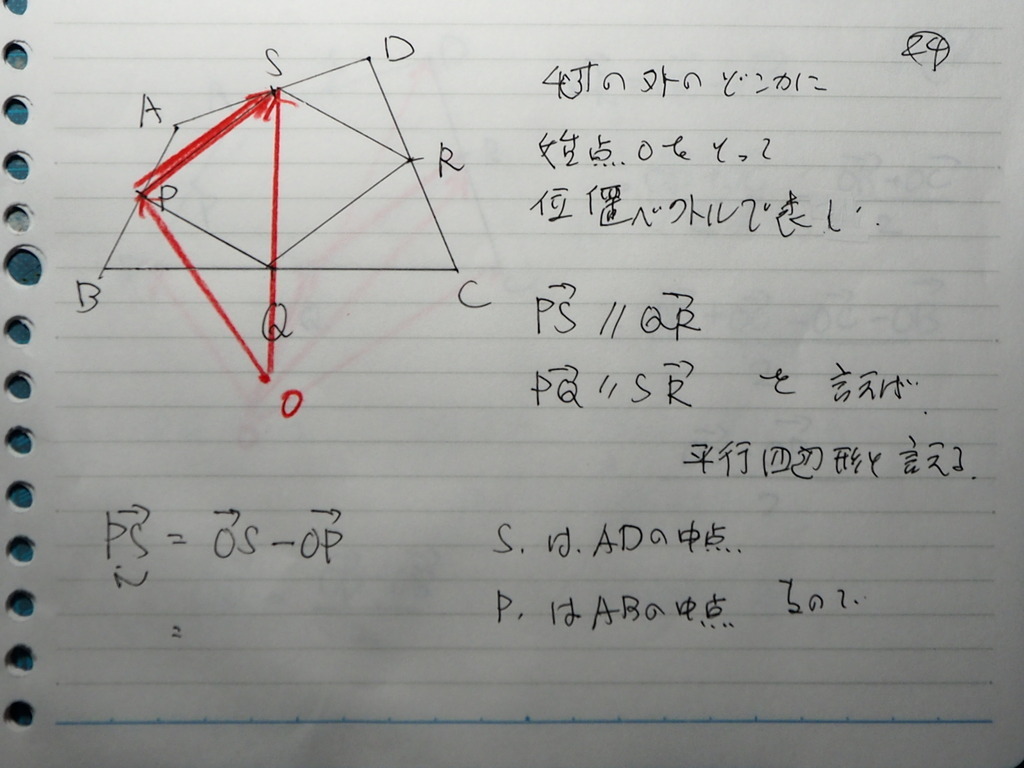
24
なんだ こりゃ
自分で書いたのに
読めない
要するにですね
ABCDPQRS いがいの どこかに
点O を とって
位置ベクトルで
考えると
対辺が 平行であること
言えばいいんだから
( 平行で 大きさが おなじ )
25
対辺を 調べてくでしょ
PS と QR
まず PS から
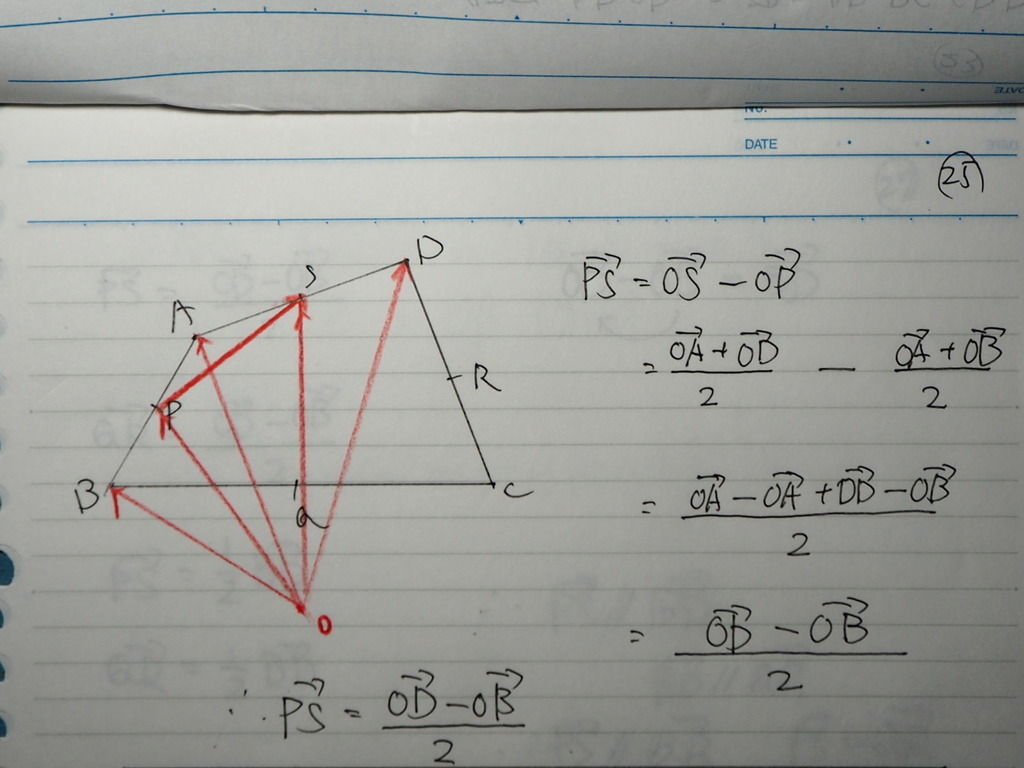
26
QRは
おなじだ
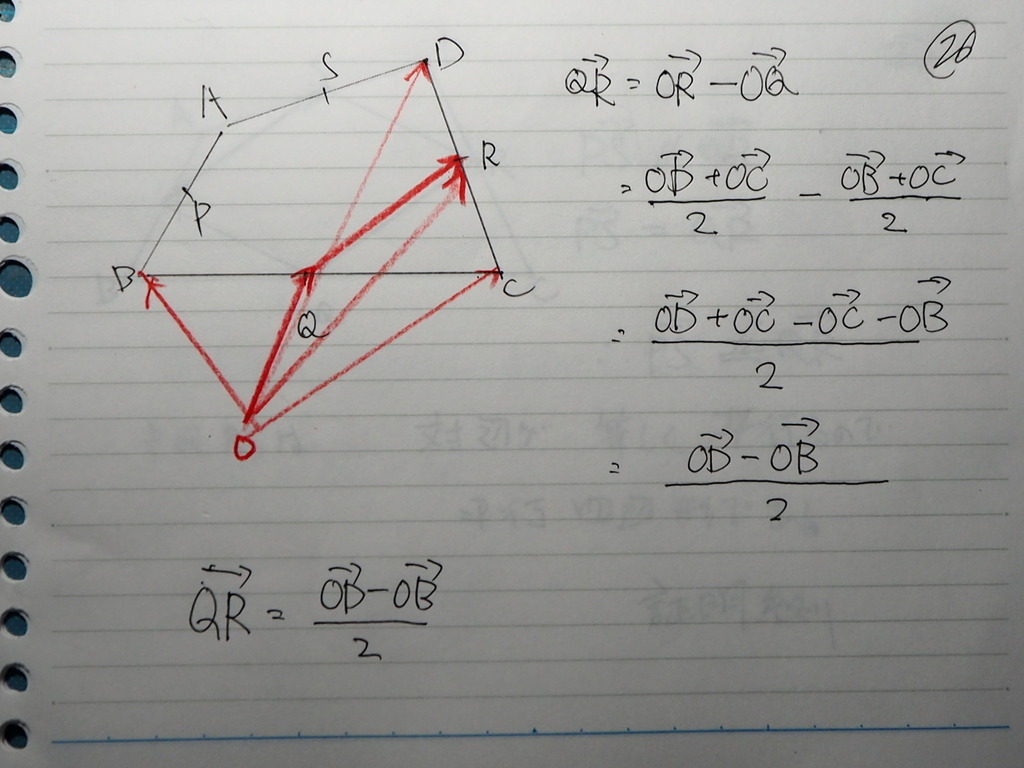
27
というわけで
PS 平行 QR
PS = QR
( ベクトルは 平行移動できる )

28
PQRSは 平行四辺形
29
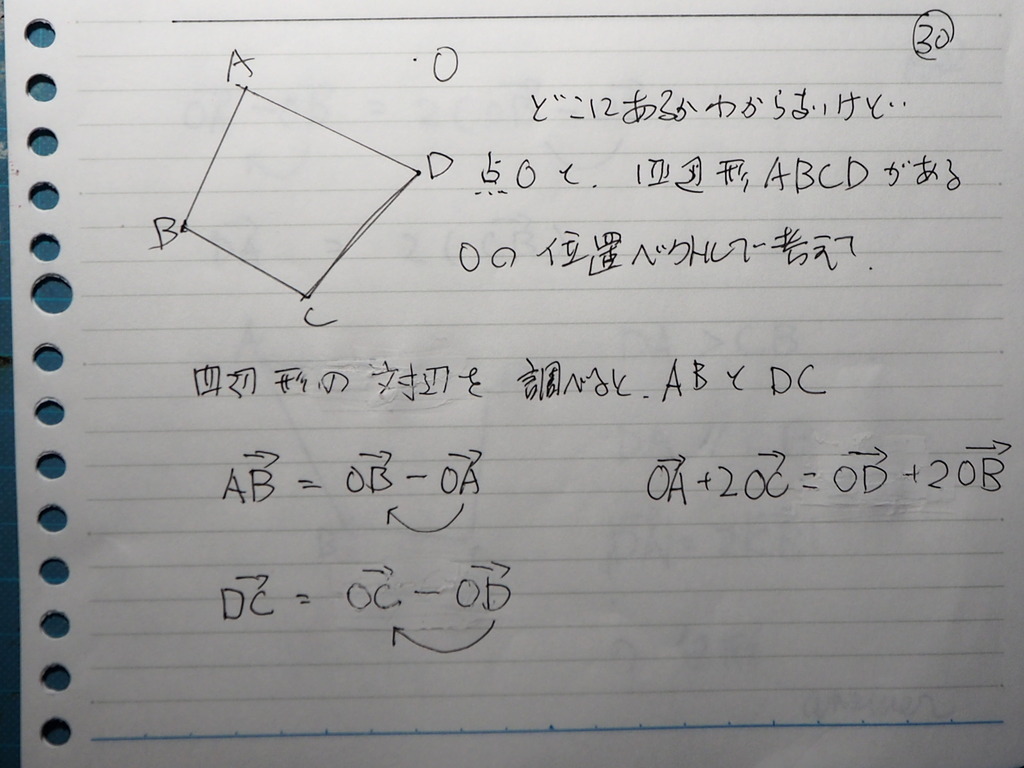
4辺形 ABCD と 1点 O があって
OA + 2OC = OD + 2OB
である この4辺形の 形状は何?

30
対辺を 調べればさ
AB と DC
条件は これだから
んん~
31
条件式の方から
対辺を 出してきた方がいいから
やっぱりさ
対辺を AD と BC にして
考えると
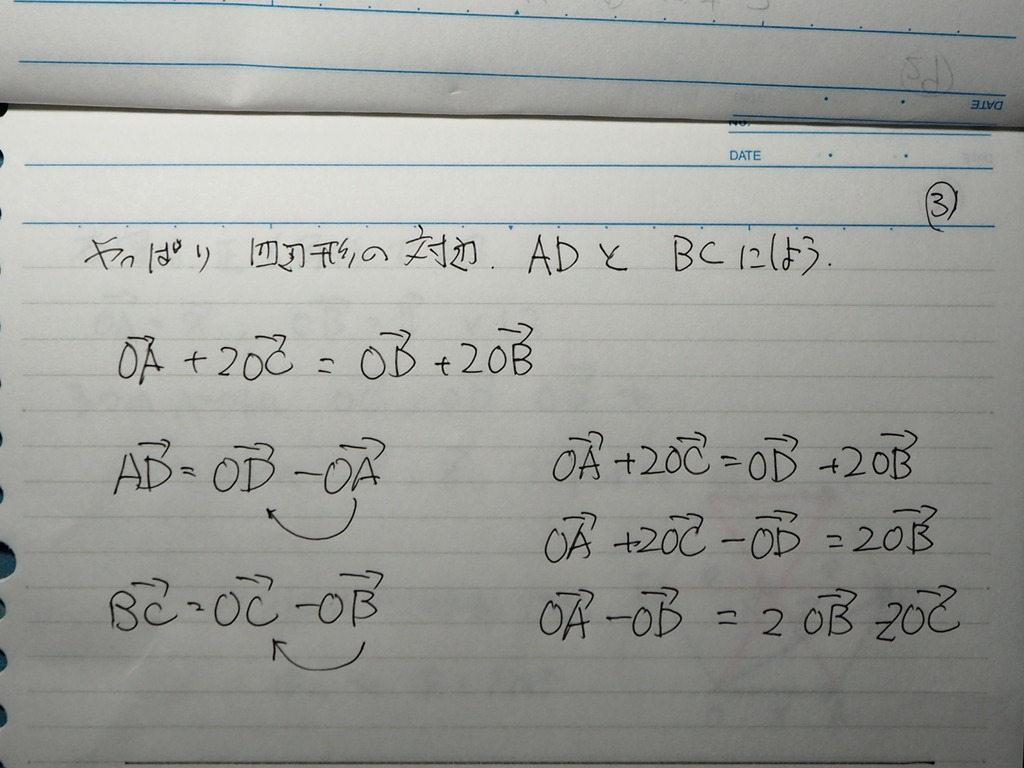
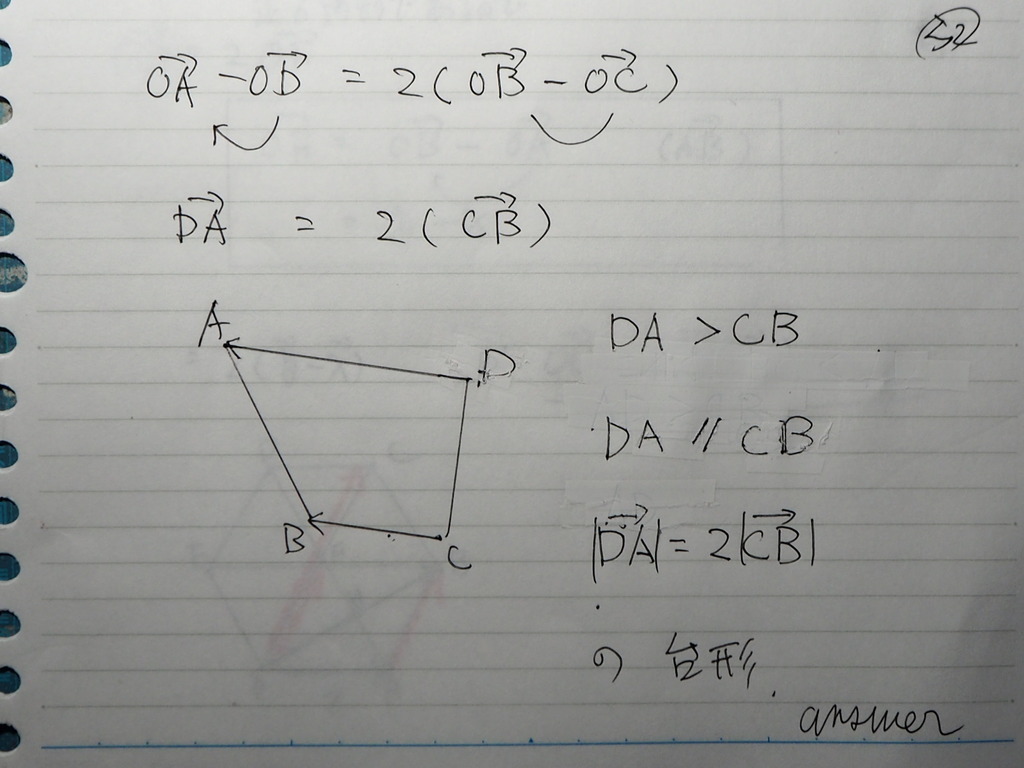
32
条件式を 変形して
対辺を 作ってくと
対辺が 実数倍
対辺が 平行で
大きさが ADが BCの 2倍
な 台形 だね
33
正6角形がありました
OABCDE です
OA=xベクトル
OB=yベクトル
とするときに
OC,OD,OE ベクトルの
成分を x、yで表せ

34
やり方は いろいろ あります
正六角形であることと
ベクトルは 平行移動できること
ベクトルには 向きがあることを
使って
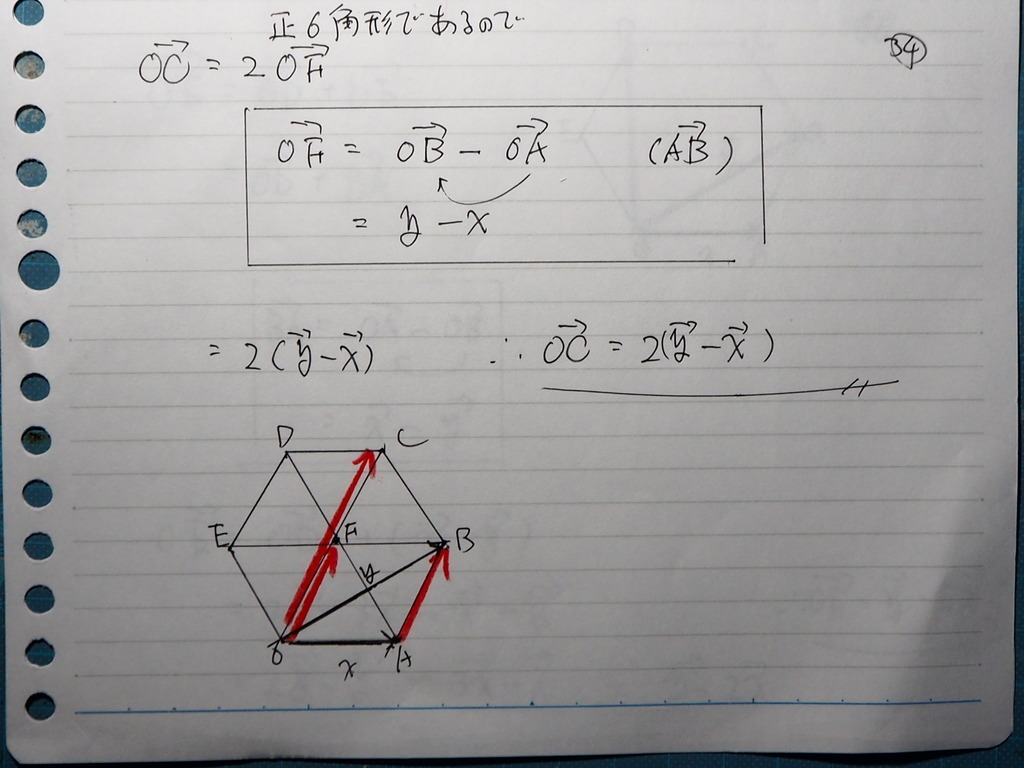
35
答えは 一つですが
やり方は いろいろあるため
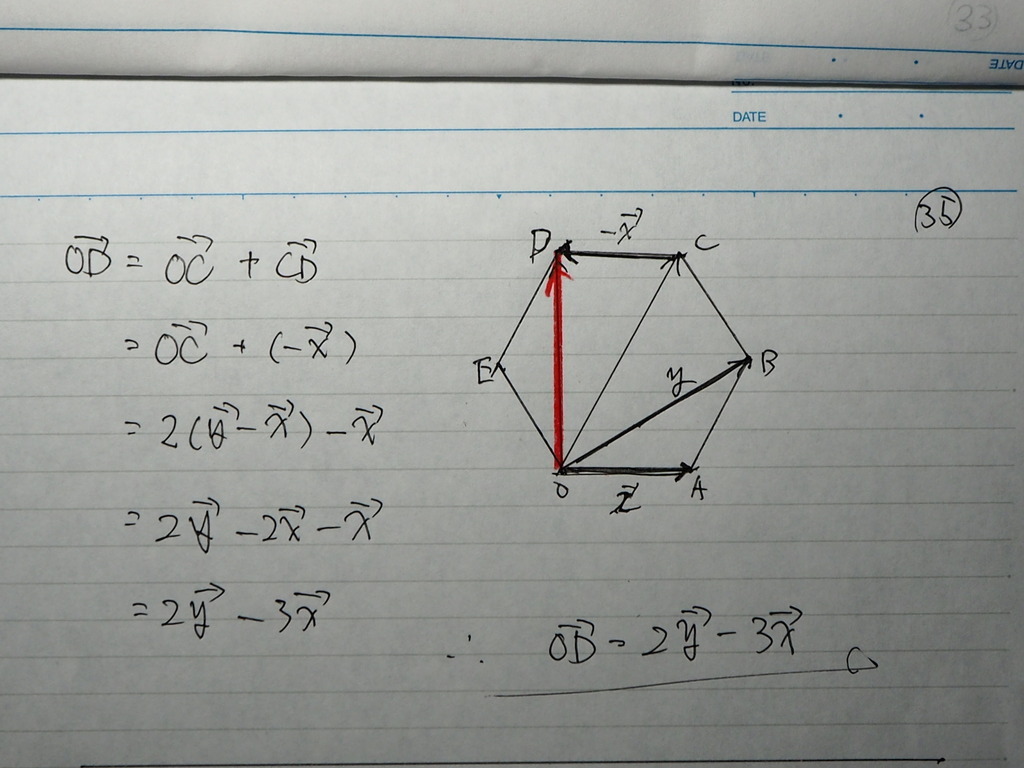
36
こんな感じに しましたが
答えは あってるって
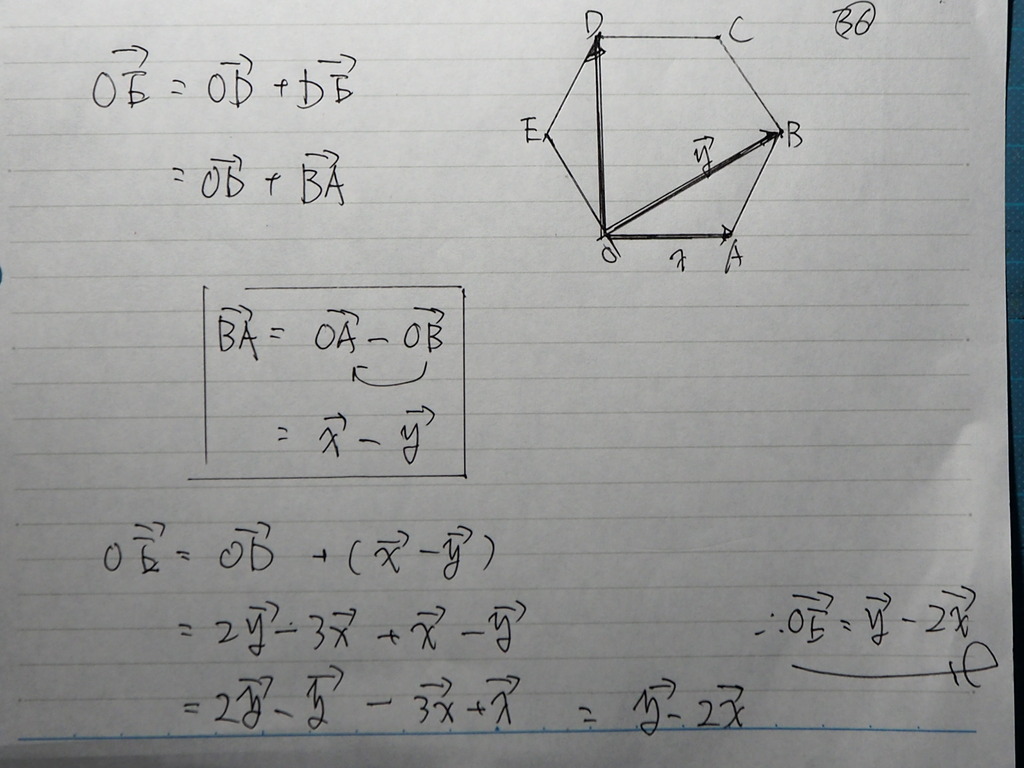
お疲れ様です。
図形とベクトル
計算の 形
和 は
ひっつ目のベクトルの 終点から
次の ベクトルを 書く
かんじに
差 は
始点の おなじ 二つのベクトルの
先に 橋 を渡す感じで
方向は 差の式の
後ろから 前の様に
02
ベクトルの 大きさは
√(x成分の二乗 + y成分の二乗 )
ふつうの ベクトル 位置ベクトル のとき
成分を 引き算して
ベクトルを 求めたときも
その 成分に関して
√(x成分の二乗 + y成分の二乗 )
03
分点ベクトル
公式は これです
04
m>0 、n>0 の時は
内分点
分母は m+n
分子は それぞれの ベクトルに
遠い方 を 掛ける
m、n が 異符号の時
どっちかが マイナスになるときは
マイナス側が
AB の 外に来て
外分になる
06
m、または n、が =0の時は
分点は A または B に 一致する
OPが 中点の時は
2分の a+b
07
三角形 ABC で 重心を Gとすると
点O を それ以外の どこかにとって
位置ベクトルで表すとき
OGベクトルは 1/3( a+b+c)
08
平行の 条件は
0でない 実数倍で 表現できること
09
垂直条件
ベクトルは 成分で書かれてますが
垂直を 判別するのは 成分の
計算で
10
共線条件
3点が 一直線上にあるとき
始点を 合わせて
実数倍 表示ができること
11
実数倍が 負になるときは
始点を 合わせると
3 点 A,B,C があるとき
Aにたいして B、 C は
反対側 どうしになる
12
共線条件
位置ベクトルを 使って
直線 L、M の 交点 P
直線 M、N の 交点 Q
の 位置ベクトル
OP = OQ
を 示す
13
これらを 踏まえまして
問題
ある 台形 ABCD があって
( 条件があります
BC 平行 AD
BC > AD )
対角線の 中点を E、F
とすれば
次のことが 成り立つことを
証明しなさい
という問題
14
まず 平行条件
平行なので
始点が 一緒では ないですが
実数倍表示ができる
さらに
条件から
実数倍の K は
K > 1
15
BD, ACの 中点を E,Fとするので
16
この時に
EF 平行 AD
EF = 1/2 ( BC - AD )
を 証明せよ
そこで
これらの 外に 点O を とって
位置ベクトルで
考えると
17
E,Fは それぞれ
BD、AC の 中点であるから
中点の 分点ベクトルで
OE ベクトル
18
同じく
中点の 分点ベクトルで
OF
で EF ベクトルは
OF-OE
19
EF ベクトルの 分点ベクトル表示で
分子の 左かっこは
BCベクトル
20
EF ベクトルの 分点ベクトル表示で
分子の 右かっこは
ADベクトル
出てきた式に
始めの 平行条件を代入したら
21
すでに ここで 答えが 出てるんですが
先に 平行であることを
言いたいので
式変形して
22
EFと ADが
実数倍表示が できたので
EF 平行 AD
そして
少し 前に戻る感じで
BC=K AD を 代入して
EF=1/2(BC-AD)
23
次は
4辺形 ABCD が あるんだけども
それぞれ AB,BC,CD,DA の 中点を
P,Q,R,S とすると
4辺形PQRSは 平行四辺形 であることを
証明しなさい と言う 問題
24
なんだ こりゃ
自分で書いたのに
読めない
要するにですね
ABCDPQRS いがいの どこかに
点O を とって
位置ベクトルで
考えると
対辺が 平行であること
言えばいいんだから
( 平行で 大きさが おなじ )
25
対辺を 調べてくでしょ
PS と QR
まず PS から
26
QRは
おなじだ
27
というわけで
PS 平行 QR
PS = QR
( ベクトルは 平行移動できる )
28
PQRSは 平行四辺形
29
4辺形 ABCD と 1点 O があって
OA + 2OC = OD + 2OB
である この4辺形の 形状は何?
30
対辺を 調べればさ
AB と DC
条件は これだから
んん~
31
条件式の方から
対辺を 出してきた方がいいから
やっぱりさ
対辺を AD と BC にして
考えると
32
条件式を 変形して
対辺を 作ってくと
対辺が 実数倍
対辺が 平行で
大きさが ADが BCの 2倍
な 台形 だね
33
正6角形がありました
OABCDE です
OA=xベクトル
OB=yベクトル
とするときに
OC,OD,OE ベクトルの
成分を x、yで表せ
34
やり方は いろいろ あります
正六角形であることと
ベクトルは 平行移動できること
ベクトルには 向きがあることを
使って
35
答えは 一つですが
やり方は いろいろあるため
36
こんな感じに しましたが
答えは あってるって
お疲れ様です。
2020年06月24日
大人のさび落とし 008 ベクトル 正多角形
01
大人のさび落とし
三角形 ABC があって
正三角形だって
ベクトル AB + BC + CA の
成分を 考えて
cos Θ + cos (Θ + 120°)+
cos( Θ + 240°) =0
を 証明せよ。
02
三角関数 で
加法定理 ってのが 計算方法として
あるのだけれど
実際計算すると =0 になるんですが
それを 使わずに
ベクトルの 成分を 利用して
証明してください
と言うものです。
ちなみに
加法定理は
03
cosの場合は
こんな感じで
展開して行って
04
値が 出てるとこを 数値に 直すでしょ
こんな感じで
05
ね 計算すると =0
になる
はい
じゃー なくってですね
答えは そうだよ
ベクトルの 成分を 考えてさ
06
正三角形がありました
ABC です
ここで
一辺の長さを 1としよう
そうすると 楽だから
その前に
三角形の 辺を ベクトルで
1週 足し合わせると
元に 戻ってくる
0 ベクトルでしょ
零ベクトル の成分は (0,0)そこで
07
正三角形 ABC の 頂点の一つAを
原点に 置いて
∠XOB を Θ にすれば
正三角形の 1辺を 大きさ 1としたから
08
たとえば aベクトルが
x軸と なす角が Θ
だとしたら
あったじゃナイスカ
ベクトルの大きさは
ベクトルの x 成分は
ベクトルの y 成分は
09
それを 用いて
ABベクトルを 成分の計算をすると
x成分は cosΘ
y成分は sinΘ
10
次に
BC ベクトルなんだけど
x軸との なす角を 考えると
Θに 120° 足した形
B に x軸と 平行な 補助線を引けば
同位角 + 120度
それを 踏まえて
成分の計算
11
CA ベクトルも
x軸との なす角を 考えると
12
Cに x軸と 平行な 補助線を引けば
Bがなす角の 同位角 +120°で
成分を 計算すると
13
成分は こんな感じ
14
で ベクトルを 成分で
足し算すると
15
x 成分が
もろに 証明せー
の 式に なってて
16
先に 計算しておいた
正三角形 ABC の 辺を 使った
足し算が =0 だったから
与式は =0 になる
ちなみに
y成文も =0 になる
17
この問題は
正三角形ABC の 重心を O として
原点に 取り
OA+OB+OC=0 を 使っても
証明できる
18
重心のところで
似たようなのが あるから
こんがらがらないように
これ と これ
見たいのがあってですよ
19
重心を O として
原点に取るほう
正三角形 の 性質を 利用して
角度を 計算
それから
重心から 各頂点までを 半径1とする
円を 書くと
20
こんな感じになります
21
そこで
ここまでで
紙面で計算してきた成分を
足し合わせた ものが =0なのだから
へ 持ち込んで
22
こんな かんじで
23
今度は 成分を 計算してね
24
OAは x軸上だから
(a、0)
AB を 行く前に
OB を 求めて
AB= OB-OAを 使おうと
25
ベクトルの 大きさと なす角が 分かれば
成分が 計算できるから
26
ところで
題意では OB 出はなくて BOベクトル
なので
BO ベクトルは 向きを 180度変えて
で
AB ベクトルの方は OBーOA を 使って
27
こんな感じ
28
最後に
正五角形の問題
29
2π/5
ってのは 72ど
30
作図していてですよ
正五角形は
丁度 ここがさ
72°になるじゃ ナイスカ
一辺の長さを 1とすれば
Aを 原点に 重ねて
ABを x軸上に とれば
成分 一つ目は AB(1,0)
たぶん cosの 成分が 証明に
使えるんですね
31
順次
なす角を 同位角で 動かしながら
それぞれの ベクトルの x軸とのなす角
を 見ていくと
紙面での成分計算の様に
なってきて
32
正多角形を 一つの角から
順に 元のとこまで
一周 ベクトルで 足すと
零ベクトル になるので
その時に
33
なるでしょ
34
その時に
成分を見たら
あ 証明できた
お疲れ様です。
( 晴れ部屋へ 家庭菜園と ざっかや
メニュウ ページ リターン )
2020年06月22日
大人のさび落とし 007 ベクトルの 大きさ
01
ベクトルの大きさ
問題
3定点があって
その他に どこかに 動点Pがいる
PA +PB +PC の ベクトルの和の
大きさが 3であるとき
動点P は どんな 軌跡になってますか
という問題
02
ここで
成分 で書いてある ベクトルは
原点O の 位置ベクトルと
同じ意味なので
位置ベクトルで
書き換えて
03
動点Pを P(x,y) と置けば
ベクトルの 引き算で
PA PB PC ベクトルの 成分が出るので
04
こんな感じで
05
この3つを 足し合わせて
出来た ベクトルを
06
ベクトルの 大きさを 計算すれば
これが =3 なんだって
07
これは 円の 方程式だね
原点を 中心にした
半径1の円が
動点pの軌跡
08
次は
やはり
動点P の軌跡を 求めるんですが
2つ あります
09
位置ベクトル 表示にして
計算して
10
それぞれの ベクトルの大きさが
等しいのだから
11
計算してくと
12
なんかさ
直線の 方程式になったと
答えは これでいいんだけど
これってなに
13
余り 複雑でないので
少し計算すると
Pの 軌跡は
y切片が 1で 傾きが -1
の直線
14
2点 A,B の方は
2点を通る直線の公式で
y=x+1
15
2直線の傾きを 書けると -1
なので
直交していて
直感で
なんか ABの 真ん中辺かな
16
そこで
2直線の 交点の座標を
出すでしょ
17
線分ABで
中点の座標を 計算するでしょ
18
同じじゃナイスカ
ABの 中点を通り
直交してるので
Pの軌跡は
ABの垂直二等分線になっていた
19
もう一つ あるんですが
こっちは
さっきの PA PB ベクトルの
成分を
20
足して
大きさを 計算すると
21
辺々2乗して
22
式変形で
23
これは 中心が (0,1)の 半径1の円
24
次はですね
ちょっとこじゃなく
わかんなくて
とらを 見ました
たしかに こうすれば
出るんだけど
そこへ もってく
数学的な カン とか
もののみかた が
まだ ピーンとこない
んん~
兎も角行ってみましょう
25
まず
2つの 動点の x成分
出会うとこを γ
26
2つの 動点の y成分
出会うとこを δ
Qの速度ベクトル の 大きさは 5で
これらから
関係式が 3っつ
これだけなの
27
そしたらさ
➀から
28
②から
④、⑤と二つ式が出て来て
29
T>0
個々が味噌なんだけど
こんな感じにして
等号が成り立つので
30
係数を 比較したら
でてしまったと
31
大きさは あってるでしょ
出た値を 使って じゃナイスカ
32
T=3
γ(ガンマ) と (デルタ)δ は
7と12
33
まとめるとこんな感じで
お疲れ様です。
( 晴れ部屋へ 家庭菜園と ざっかや
メニュウ ページ リターン )
大人のさび落とし 006 ベクトルの成分
01
ベクトルの成分
aベクトル:
座標平面上の 原点 O を
始点とする ベクトル
OA=a ベクトル
とする時の 終点Aの座標 ( a1,a2 )
を ベクトルの 成分という
02
ベクトルの 成分は
aベクトル= (a1,a2) とかく
任意の ベクトル a の
x軸 、y軸 への
正射影 の 大きさの 組み ( a1,a2 )
の事である
03
ベクトルの大きさは
次の 式で 求められ
04
ベクトルと x軸の なす角を θ とする時
ベクトルの 成分 a1,a2 は
ベクトルの 大きさと
なす角 θ を使って
表すことができ
05
x軸 成分のa1は
ベクトルの 大きさと cos θで
06
y軸 成分のa2は
ベクトルの 大きさと sin θで
07
こんな感じに
08
まとめると こんな感じに
求めることができる
09
基本ベクトル
x軸 、 y軸 の 正の向きと 同じ向きの
大きさ1の ベクトルで
基本ベクトルと言い
成分の時のように
e1,e2 や i,j
で 表す
( 専門書は i,j で書いてあることが多い )
10
ベクトルの成分の 計算は
成分 ごとの 計算になり
こんな感じ
11
ベクトルが 成分で 表されていれば
ABベクトルは
次の場合
ベクトルの引き算で
成分を 計算した形で
ベクトル の 大きさは
こんな感じに 書ける
12
O ,A ,B が 共線 の条件は
各成分が 実数倍に 成っていること
こんな感じに
分点の ベクトルは
成分ごとに 分点ベクトル の 公式
位置ベクトルは
始点O が 決まっているとき
aベクトル = OAベクトル
13
以上を 踏まえまして
問題を 行ってみましょう
14
計算ミスを しないように
成分の x成分 y成分
ごとの けいさんだよ
15
計算ミスしないように
工夫していただいて
16
次の 実数倍は
同じ 平面上に
大きさや 向きの違う
二つの ベクトルがあると
そのベクトルの 実数倍を使って
平面上の 全ての ベクトルが
表現できる を
実際に 計算する問題で
aベクトル と bベクトルの 実数倍を使って
cベクトル を表現するときの
実数倍 m, n,を 計算してみましょう
17
成分ごとの 実数倍 表示に
成分を 代入して
式が 2本 分かんない 文字が 2つ
18
m の方を 消去の形で
nを 求めると
19
n=1
もとの 式➀’ に n=1を 代入して
20
m=1
実際に 入れて見ると
なるでしょ
21
(3)は
さらに 平面上の ベクトルを
2つ づつ 使って
新しく 2つの ベクトルを 作ったんですが
片方に 実数倍kが 入ってるうですよ
この k を
二つの ベクトルが
平行になる様に 調節したい
22
平行 だけを いうならば
一方の ベクトルが 他方の ベクトルの
実数倍に なっていればいいので
まず くらべる 2つの ベクトルの
成分を 個々に求めてじゃナイスカ
23
整理して
この 2本の ベクトルの
各成分が
同じ 実数倍に 成るように
調節すると
24
まず
式が 2本 文字が 2つ
なので
解けるんですが
実数倍は なんばいか
まず m を求めて
25
計算を
26
mは -1/2 か
話は 72度っ位 ずれるけど
かとり は 線香派? ベープ派?
27
話を 元に戻して
m=-1/2を 元の式に 代入して
28
上の 方に するか
k=-1/2
29
実際に k=-1/2 を 代入したら
ベクトルが 実数倍 (m=-1/2)
になってるか 見てみると
30
なってますね
31
問題
平面上の 2つの ベクトルの
実数倍で
3つ目の ベクトルを 表現する問題
32
(1)の方は
平面上の 全ての ベクトルは
2つの
向きや 大きさの 違う
ベクトルを 使って
表現できる
33
まず 型に はめて
成分を 代入
34
式が 2本 文字が2つ
計算して
L=-1/2
35
➀に L=-1/2 を 代入すれば
k=-7/2
36
ややっこしけど
実数倍の 式に それぞれ
K, L を 代入して 計算したら
Cベクトル に 成ったでしょ
37
(2)
この平面上の ベクトルは
適当な 実数 x、y を使って
x aベクトル +y bベクトル
の 形に なることを
証明せよ
38
そこで
この平面上の
任意の ベクトルを
B(p,q) として
ここで大事なのは p、qは 実数を明記
適当な 実数 x、yが 実際に
存在するか 計算すべく
型に入れて 計算するとですよ
39
今求めてるのは
p、qは 任意の 実数で
実数倍の x、yが 存在することを
調べてます
x、yを 求めて
p、q が そのまま入っていても
p、qが 実数なので
一定の 式に 成れば いい
40
x を 消去で
y を 任意の 実数ということに
なってる p、qで 表すと
➀に yを代入して xを 求めると
41
p、qは 任意の 実数ですが
x、yが 一定の 式に 成ったでしょ
42
だから こんな感じの 実数倍の 式で
この平面上の 全てのベクトルは
aベクトル bベクトルの
実数倍の和の形に
表現できる
実際に
aベクトル bベクトル に この x、yの
実数倍表示を
計算したら
43
ねー
任意の ベクトルに 成るでしょ
44
今度は 平行の問題
45
平行か 見る 二つのベクトルの
成分を 計算しておいて
実数倍に 各成分がなってればいいので
ベクトルが 2本
1本目の 成分は
46
2本目の成分は
これらが 実数倍の 関係に
なってれば 平行だから
47
式が 2つ 分かんない文字が 2つ
解けるんですが
まず 実数倍の mから
これが 存在してれば 平行だ
48
mを ➀式に
代入したらば
49
x=1/2
50
次は
乱筆 で すみませんが
問題文を 読んでいただいて
題意より
二つのベクトル
aベクトル と bベクトル がある
bベクトルは
aベクトル の 2倍の 大きさである
aベクトル と bベクトル の
なす角は π/6 である
aベクトルの 成分は (√3、1)である
51
普通ベクトルの なす角と言ったら
x軸との 角度 なので
で
成分が 出ていれば
ベクトルの大きさを 求め
それぞれの cos sin を
含んだ式が
aベクトル の 成分に等しいので
共通の θを 探して
なす角が 一つに決まる
52
問題では
aベクトル bベクトル のなす角と
言っていて
これは x軸との 角度の事ではない
aベクトルは 成分が 出ているので
x軸とのなす角を 求めることが
できるから
まず aベクトルの 大きさを 求め
53
この aベクトルの cos シータ
が √3
この aベクトルの sin シータ
が 1
なのだから
54
単位円を使って
共通の θを 探すとじゃナイスカ
aベクトルの x軸との なす角は
丁度 これも π/6
55
だから aベクトルのなす角は 30ど
π/6
bベクトル は aベクトル と
やはり 30度 π/6 をなし
大きさは 2倍
56
aベクトルの 大きさが 2なのだから
bベクトル の 大きさは
4ということになる
57
aベクトル と bベクトル
は なす角が π/6
30度 で 2通り 考えられる
x軸上の 重なる方は
ベクトルの大きさが そのまま x成分
y成分は 0 だから
58
bベクトル
1本目は (4、0)
もう一方は さらに
aベクトルに x軸から π/6
30ど 増し加えた形
π/3
60度
59
ベクトルの大きさが 4 なす角が
bベクトル の x軸とのなす角が
π/3 60度
と分かれば
60
bベクトル の x成分 は b1=2
bベクトル の y成文 は b2=2√3
61
ナタメ
bベクトル の 成分は
( 4, 0 ) または ( 2, 2√3 )
お疲れ様です。
( 晴れ部屋へ 家庭菜園と ざっかや
メニュウ ページ リターン )
2020年06月20日
大人のさび落とし 重心ベクトル 005
01
平面の重心ベクトルに関しまして
重心って何
紙型 の 重心を記して そこを
糸でつるせば つり合うってやつ
3角形⇒ こんな感じでした
三角形ABCの 角A の 対辺BC の中点を D
とすれば
ADを 2:1 に内分したところが
重心
02
ベクトルに 位置ベクトルっていうのがあります
始点 O の位置が決まってるとき
三角形 ABC の 各ABC を 位置ベクトルを使うと
OA OB OC ベクトル になる
03
問題ですが
三角形ABCの 重心をG とする時
位置ベクトルを使うと
重心の 位置ベクトル OGは
次の様に なる
事を 証明する問題
04
そこで
いままで 知ってる 知識で
重心は 三角形 ABC の場合
BC の 中点 D を 書き加え
AD を 2:1 に 内分したところだから
この G を OG ベクトルとして
05
OG ベクトルは OA ベクトル ODベクトルの
分点ベクトル
06
分点ベクトルの
公式に 入れて 計算すると
OP ベクトルは
aベクトルに 遠い方の n倍
bベクトルに 遠い方の m倍
だから
07
計算したら
こんなデショ
で
題意では
OG OA OB OC しか使ってなくて
ODは 都合で 書き足したものだから
ODを 使える ベクトルで
置き換えるべく
08
ODベクトルは
OB ベクトル OC ベクトルの
中点の分点ベクトル
だから
09
出てきた ODベクトルを
さっきの OG ベクトルの式に 代入すると
10
何ので
三角形の重心を
位置ベクトルで表すと
任意の ( どこでもいい ) 点 O
に対する
各頂点の位置ベクトルの 和 に
1/3 倍したものになる
11
(2)は いま 証明したものの 証明なんですが
こんな感じで
位置ベクトルに 書ける とき
G は 重心であることを
証明せよ
仮に 重心をG' と置いて
この式を 使うと
こうなるんですが
これが 重心です
12
ところで さっき (1)で
三角形ABCの 重心を 位置ベクトルで
表したものと
OG' は 同じくなる
G と G' は
同じ点だ
ゆえに
三角形 ABCの 重心は これこれ
と持って行くようです。
13
今度も 位置ベクトルなんですが
OA + OB + OC = 0
⇒ O は 重心であることを 証明せよ
14
普通に 考えれば
三角形の 重心は
三角形の 内部にあるはずなので
15
こんな感じに 図に書いて
三角形のABCの重心は BCの 中点Dに
Aから 線を 引いて
ADを 2:1に 内分だから
そのときの
BCの中点D の 位置ベクトルの
分点ベクトルは
16
これを
条件式に 代入して
そうすると
今度は
題意には なかった Dが残るんだけど
17
何かに 似てませんか
見え隠れしてる
18
こんな感じにしたら
ADを 2:1に 内分してるよ
ここで大事なのは
AOD が 一直線上にあることを
証明すること
ベクトルは 平行移動できる
ベクトルが 等しいということは
とても大事なことで
19
AO ベクトルと 2 ODベクトルは 平行
AOベクトルの大きさは 2倍のDOベクトル
点Oを
重ねると 一直線になる
20
A O D は 一直線上にあり
AO : OD = 2:1
つまり O は
三角形ABCの 重心である
21
次は
問題を
読んでもらって
正三角形上に
P,Q,R と言う 定点があり
ソレゾレ
同時に 同じ速度で
BC CA AB 方向に 移動して
その時の 点を X 、Y、 Z で 表すときに
この しばらく 動く 三角形XYZの
重心は 定点に 成ってることを
証明して チョーだい
という問題。
22
三角形XYZの重心が 定点であることを言うには
初期の状態が
三角形PQR なのだから
三角形PQRの 重心と 三角形XYZの 重心が
同じことを 言えばいい
23
そこで
三角形 PQR の重心を G とすれば
位置ベクトルを使って
表現できるのだから
へてから
三角形XYZの方を 考えると
24
三角形XYZの各位置ベクトルを
元の三角形PQR に 移動分
PX QY RZ を 足す形で
表して
25
整理すると
こんな感じで
26
ここで 何かしないとさ
で
PX QY RZ はそれぞれ
速さは おなじ
方向は
BCベクトル
CAベクトル
ABベクトル
方向
そこで
BC=a ベクトル
CA=b ベクトル
AB=c ベクトル
とおくと
27
こんな感じでさ
そうすれば
PX=ka QY=kb RZ=kc
な感じに 実数倍にしてじゃナイスカ
28
こんな感じに
書き換えて
あと少し
29
三角形XYZの重心をG'として
こんな感じに なると
これが
OG=OG'になればいいのですよ
30
ところで
一番元の 正三角形ABCの
それぞれの 辺を
BC=aベクトル
CA=bベクトル
AB=cベクトル
としたので
ベクトルの 足し算で
a+b+c=0
一周して 元に戻ってるでしょ
31
なので
三角形XYZの 内側の カッコ内が 零ベクトル
32
OG=OG' になったということは
三角形 XYZ の 重心は 定点である。
お疲れ様です。
( 晴れ部屋へ 家庭菜園と ざっかや
メニュウ ページ リターン )
2020年03月21日
お知らせ
お知らせ
未確定ですが
何分申し訳ないのですが
大人の さび落としは
4月 いっぱい までは お休み
5月 以降 できるだけ 速く
復活 の予定です。
方向性といたしましては
当 趣味の 数学 大人のさび落としは
今年中には 終わらないと思いますが
とりあえずの 目標てきな
第一 ゴールを 複素数とベクトル
までを 目標に
よじ登りたいと
思っております
途中から 理解が 上がってきて
加速 できればいいですが
かなり 無理があるので
なんて言えば良いカナ
・・・
兎も角
安全な youtubeも 多数ありますので
私のブログは
後回しで 良いですから
なお
当ブログの 問題は
30 年 以上前の 過去問を
中心に 構成されています。
できるだけ
順序正しく 問題を 解いていくことで
面白く 見ていただければ 幸いですが
兎に角
たいへんですので
・・・
さいさん 書きますが
途中から
後から 来る
かわいいのへの
叔父さんからの 手紙に 成ればなで やってますため
よじ登っています
何分 私が 趣味でやってますため
万が一にも 学生さんが
間違いを 犯しては いけませぬため
もう一回 勉強 しなおしています。
( 晴れ部屋へ 家庭菜園と ざっかや
メニュウ ページ リターン )
2020年03月19日
大人のさび落とし ベクトル004 分点ベクトル
ベクトル 004 分点ベクトル
その前に
お詫び
003 で
対角線が 先にあったので
対角線上に 点を取った
ことから
一直線を いきなり 言ってましたが
ベクトルが 平行で かつ
ABベクトル = k AC ベクトルだから
A,B,C が 一直線上にある
の様に 書いた方が
安全かと
004 では そういった書き方に 成っています。
01
三角形 ABC
で
AB=p ベクトル
AC=qベクトル と する時
(1)AC の 中点を D とする時
BDベクトルを
pベクトル 、qベクトル で
表せ
(2)
BC を 2:1 に 内分 する点を
E とする時
AEベクトルを pベクトル 、qベクトル
で 表せ
(3)
BDを 4:1 に 内分 する点を F
とする時 AFベクトル を
pベクトル 、 qベクトル で表し
A,E,Fは 一直線上 にあることを
証明せよ。
02
ベクトルの 引き算の 定理を 使って
ABベクトルは pベクトル
ADベクトルは qベクトルの 半分だから
03
これを 定理通り 計算すると
BDベクトル
04
(2) BCを 2:1に 内分 する点を
E とする時
AEベクトルは
分点ベクトル になってるので
定理は
05
定理 通り 計算すると
AEベクトル
06
(3)
BDを 4:1に 内分する点を
F とする時
AFベクトルを pベクトル 、qベクトル
で表し A,F,Eが 一直線上にあることを
証明せよ
一直線上にあるは
AF = k AE
を 言えればオーケイ
07
AFベクトルは ABベクトル + 4/5 BDベクトル
08
AFベクトル AEベクトル を
出してきて
09
この二つのベクトルは
同じ (pベクトル+2qベクトル )
の 実数倍同士
セオリー どおりに するには
実数倍の 係数を どちらかに まとめてしまえば
ベクトルは 平行
平行な 二つの ベクトルの 始点を合わせると
AF = K AE の 形になるので
10
k=3/5
A,F,Eは 一直線上にある。
11
三角形 ABC において
CAベクトル =aベクトル
CBベクトル =bベクトル
とする時
(1) ABを 2:3に 内分 する点P
について
CPベクトル
(2) (1)の CPを 1:2に
内分する 点 Q について
AQベクトル
12
(1)
分点ベクトルなので
定理どうりに
分母は 2+3
分子は 左右のベクトルに
ソレゾレ 遠い方を かけて
足し合わせると
13
(2)
AQベクトルは
ここに なるから
14
CQベクトル - CAベクトル
15
三角形 OAB において
OAベクトル=aベクトル
OBベクトル=bベクトル
とする
OCベクトル=3aベクトル
ODベクトル=3bベクトル
OEベクトル=2aベクトル + bベクトル
の時
3点 C,D,Eの位置関係を
図示せよ
16
作図 していきますと
DEベクトルと DCベクトルは 平行な ベクトル
始点を 重ねると
DE= k DC
一直線上に ある
17
一直線上にあり
Eは DCを 2:1に 内分する点
18
三角形 ABC の内部に 点P があり
3APベクトル + 4BPベクトル + 5CPベクトル =0ベクトル
である
三角形 ABP BCP CAP の 面積比を
求めよ
19
3つの 小さな 三角形は 大きな
三角形ABC の 内部にあるので
大きな 三角形ABCと 各 内部の 三角形を
面積比を くらべながら
三角形ABC を 基準に 面積比を 出そうと
20
三角形ABC と 三角形ABP において
条件式を 両辺 7 で割って
さらに 少し 式変形すると
21
ABを 4:3に 内分する点を D とすれば
DPベクトル は 四角く 囲った ところ
22
5/7 CPベクトル = PD ベクトル なので
CPベクトル 平行 PD ベクトル
点Pを 重ねると
23
PDベクトル = 5/12 CDベクトルで
一直線上に D,P,C がある
三角形 ABC と 三角形 ABP は
底辺が AB で 共有していて
高さは DC DP の 比に 等しいので
面積は 三角形 ABCを 1 とすれば
三角形ABP は 5/12
24
同様に
三角形BCA と 三角形BCPで
条件式を
また 変形して
今度は 9で 両辺を割って
少し 変形して
25
四角く 囲った 分点ベクトルは
EPベクトル
26
AP ベクトルと PEベクトルは 平行で
点Pを 重ねれば 一直線上になるので
27
面積比は おなじ BC を 底辺にする
高さの比が AE PEの 三角形なので
28
三角形 BCAを 1にすれば
三角形 BCPは 1/4
29
三角形 CAB と 三角形CAP についても
条件式の変形で
今度は 8で割って
30
8 で割ったことで
分点ベクトルを 作りだし
31
BPベクトル と PFベクトル は
平行
点Pを 合わせれば
一直線
32
三角形CAB と 三角形CAP は
CAが 共通ていへんなので
BF PF が
高さの 比になる
33
三角形 CABの面積を 1としたら
三角形 CAPは 1/3
34
であるから
三角形 ABP : BCP: CAP = 5:3:4
お疲れ様です。
( 晴れ部屋へ 家庭菜園と ざっかや
メニュウ ページ リターン )
2020年03月14日
大人のさび落とし ベクトル003 ベクトルの実数倍。
大人のさび落とし ベクトル003 ベクトルの実数倍
ベクトルの実数倍
01
ベクトル と 実数 の 積 は
02
ベクトル の 平行条件 & 共線条件は
03
ベクトル の 実数 計算は
04
昔話
ベクトルは
平行移動で 合成できる
05
a ベクトル 、 b ベクトル があり
どちらも 零ベクトル でなく
また
同一 方向でも 、 正反対でも ないとき
この平面上の 全ての ベクトル は
この a ベクトル 、 b ベクトル の
実数倍 の 和の 形で 表現でき
06
次のようなことが 言える
07
分点 ベクトル
08
中点ベクトル
09
外分ベクトル (1)
10
外分ベクトル (2)
11
この考え方は 大切で
a ベクトル 、 b ベクトル に「分けて
書くと
12
これを R + S = 1
T + (1-T) =1
と置き換えると
分点ベクトルは こんな感じに 表現できる
13
問題
14
AB を 2:3 に ない分する点P と
a,b ベクトルの 向きを 考慮に入れて
PA 、 PB を cベクトルで 表すと
一直線上で 正反対に 2 と 3
15
対辺の DC も 同じように
今度は dベクトルを 使って
a,b ベクトルの 向きを 考慮に 入れると
DQ=2d CQ=-3d
16
PQベクトルを 四辺形の 半分から 上側と 下側で
a,b,c ベクトル を 使って 表現すると
こんな感じで
ソレゾレ 3 倍 、 2倍 して 足し合わせると
17
これを PQベクトル = にしたらば
出ましたよ
18
同じ問題を
今度は BD を 3;2に 内分 する 点R を 使って
求めると
相似形だからですよ
こんな感じの 比の値
19
分かちゃ いるつもりなんですが
正確に やってよ なんて言われると
ちょっと かゆいとこがあるから
孫の手を 探してですよ
あ これこれ
20
ウ ですか
台形も ついでに
で
21
ウ だからさ
PR の 大きさは こんな
大きさで やってしまったけど
22
同じように RQ の大きさは こんな
だから この 二つの ベクトルを 足し算 したものが
PQ ベクトルだから
さっきと同じで
なったでしょ
23
ところで
なす角って何
これが なす角
24
次は こんな問題です
25
図を描いて
AB ベクトル と DC ベクトル の補助を
c 、 d を 使って
今回は 中点ですので
こんな感じに c、d ベクトルを 書き込んで
26
四辺形の 半分から 左側 と 右側
で
MN ベクトル 表現して
辺々たしたら成ってしまいました。
27
次は 図は ありません
問題を 読んでいただいて
28
作図すると こんなでいいのかな
29
条件式を 辺々 引いて
30
なんか 式が出て来て
ベクトルの 引き算の 定理は こんなですから
これを 少し 変形すると
31
これはさ
BC と ED ベクトルになって
これは 対辺だから
ここまでで
平行四辺形
32
もし 対角緯線の ベクトルの なす角が
直角ならば ひし形 だけど
条件式からは そこまでは 分からない
よって
四辺形 BCDE は 平行四辺形。
33
問題
34
平面上の 全ての ベクトルは 方向の 違う
零でないベクトルの 和で 全て表現できるので
色々 ベクトルを 計算して 出していくと
35
まず AE は a + b ベクトル
36
今度は BD は 2b - a ベクトル
37
ちょっと整理して
対角線の上に 一直線上の ベクトル の 形で
式が 2本
変数が 2つ
お詫び
003 で
対角線が 先にあったので
対角線上に 点を取った
ことから
一直線を いきなり 言ってましたが
ベクトルが 平行で かつ
ABベクトル = k AC ベクトルだから
A,B,C が 一直線上にある
の様に 書いた方が
安全かと
38
これを 三角形 ABFを 使って
ベクトルの和
さらに そこに
2変数の入った式を それぞれ代入
39
整理すると
これはさ
係数比較 法 みたいな感じで
40
実数倍の m と k の式が 2本
m を 消去したら
BF = k 倍の BD だから
41
ねー
BF が BD の 1/3」 になってるでしょ
3等分点 の 一つだ
42
つぎは
問題
43
条件式の ABを P を 使った式に
セオリー どうりに 変形すると
AB が こんなだから
44
これをさ
整理してくと
45
んんー よくわかんないな
46
方向は 同じ方向 で 、 PCは APの2倍
APC の順に AP と 2倍のAP の長さを
AP に PC を P点 で つなげて 見ると
Pは AC を 1:2 に 内分していた。
私は クリスチャン
この世の年は 言いたくないけど
おじさんです
頭良く無いんだけど
主に 助けられてですよ
栄光在主
年上なの
若く見られたいもんだからさ
とし した
人は 永遠を 願う。
だから 人を 祝福できる 人に 成りたいね。
( 晴れ部屋へ 家庭菜園と ざっかや
メニュウ ページ リターン )
2020年03月12日
大人のさび落とし ベクトル002 ベクトルの大きさ
ベクトルの大きさ
01
ベクトルの大きさに関して
ベクトルは 大きさと 方向をもっていて
絶対値を付けて書くと
大きさを 表す
そこで 問題
一辺の長さが 1の 正六角形
ABCDEF において
AB=a , BC=b, CD=c
とする時
( ベクトルの 書き方を 省略してます )
次の ベクトルを 作成し 大きさを
求めよ
02
正六角形なので
順次 a ,b, c
とベクトルを 書き込むと
その先は
対辺に平行で 大きさが同じだけど
向きが 正反対
の マイナス ベクトルのなる
それを 踏まえて
平行移動 して 作図 しようと
ベクトルの 足し算 引き算
は こんなだから
03
で 絶対値を つけて
大きさだけ求めれば
辺2本ぶんで 2
次は
少し 補助線を 書いて
交点を G とすると
正三角形が
こんな感じで
ベクトルの 書式で
足し算を してくと
04
AAベクトル 始点と終点が くっついてる
零ベクトル 大きさは 0
05
3番目も
ベクトルを 書式で 計算して
06
補助線を くわえ
最終的なとこは DHベクトル 大きさは2
07
次は 正方形です
問題
08
たせば
対角線なのだから
大きさは √2
09
引き算の ときは
定理通り
始点を 合わせて
そうすると DBベクトル
10
大きさは √2
定理はこんな感じで
おぼえてますが
11
次の 式を 証明せよ
何か 違うところで
見かけて
苦労した思い出がありますが
12
3つに 場合分けして
➀
a、b、 ベクトルが 平行でないとき
三角形 ABC を 使って
13
三角形になるためには
長さが 短かったり 直線に
なったりしないように
14
②
a,b,ベクトルが 向きが同じ時
右側が = になる
15
③
a,b,ベクトルが 向きが正反対の時
左側が = になる
16
全て =0 の時は a,または bが =0の時
17
次は
問題を 読んで
当時 この問題に
図が ついていたか いなかったか
は 分かりませんが
図が ついてないと
難しくなる
18
幸い
今回は 初めから 図がついていて
19
なす角は
この辺は 中学生の方が
頭の 回転が 速いと思われます。
群馬の 高校入試問題
イマハ あんななんだ
難しくない?
テレビの 前なら 安心してられるけどさ
大変だったですね
で
20
次も 図があるので
作図してですよ
ちょっと 不正確すぎるので
21
もうすこし ましに書くと
22
だからにして
√3倍
お疲れ様です。
( 晴れ部屋へ 家庭菜園と ざっかや
メニュウ ページ リターン )
2020年03月11日
大人のさび落とし ベクトル 001
スローライフ の 森
3.1シー メニュウ ページ。
@ ? 前 休憩
大人のさび落とし
ベクトル
01
大きさだけを 持つ量を
スカラー
といいます
ちからー とでも覚えればさ
でも
スカラー だ からね
02
スカラー 量に 方向性が ついてくると
ベクトル と呼ぶようになります
表現の仕方は
やじるしを 上につけたり
03
ベクトルの スカラー 量は
絶対値 の様に 書いて
大きさを 表します
速度 ベクトルの スカラ量は 速さ
04
ベクトルで
方向と スカラ―量が 等しいものを
等しいといい
向きは 平行
大きさは おなじ
これは 当たり前のようだけど
すごく大事なとこで
05
再度 確認いたしまして
で
れい ベクトル
方向に関しては 考えられない
数のゼロとは 違うんだけど
06
大きさが おなじで
方向が 正反対だと
逆ベクトル
マイナスを つけて
07
ベクトルの和
ベクトルは
大きさと 向きが 等しければ
等しいのでした
そこで
平行移動 して
都合の良いところに 持って行っても
OK なので
平行四辺形の 対角線で 考える方法
( 始点を 揃える時 )
08
三角形法
一方の ベクトルの 終点に
他方の ベクトルの 始点を
平行移動して
和にする場合
09
点の 書き方の 違いで
文字は 違うけど
言ってることは おなじ
10
ベクトルの差
平行四辺形方では
始点を 揃えておいて
bベクトルの 逆ベクトルを
a ベクトルの 終点に 足し合わせて
その先を あたらしく c とでも置くと
11
ベクトルの始点を 揃えて
A 引く B は
引かれる 方向に向かって
ベクトル
これは よく使います
12
次のは
平行四辺形法 と同じことなんだけど
13
ベクトルは
平行移動して 合成できる ものなのです
14
交換の法則
結合の法則
が使え
霊ベクトルを 足すと・・・・
霊ベクトルから 引くと・・・・
同じベクトルを 引くと・・・
逆ベクトルを 使って 引き算を 足し算にすると・・
15
証明問題
ベクトルの問題て
どんな何だろうね
16
図のように 平行四辺形 を 作図して
AB + CD =
CDを 平行移動したものが BEなので
AB+BE=AE
17
AD + CB =
の方は CBを 平行移動したものが DE
なんで
AD+DE=AE
左辺 =右辺
18
頭の体操
チリとり があります
1本 自由に 動かして
ごみを チリとり の外に 出してください
答えは
キットだれか知ってると思いますので
19
さっきの 証明問題を
角度を変えて
左辺~ 右辺への 橋渡しを
BD と考えて
AB CD を それぞれ
BD DB を 使って 表すと
20
これを 足すでしょ
赤括弧の 定理を 使って
21
さらに 角度を 変えて
同じ問題
与えられた 式を 変形して行きます
22
引き算の 形になりました
23
この 引き算は
セオリー 通り なので
DB
24
右辺も DB
25
これがさ
一番 面白いカナ
左辺ー右辺=0 になればいいのだから
こんな感じで
26
なる
27
次も 同じことなんだけど
二つの セオレム を 使って
28
次も
簡単でしょ
29
次は ちょっと考えましょう
30
落ち着いて かんがえればさ
こういうわけだからさ
31
最後は
昔むかしの その昔
某国立大の入試問題
30年 以上前だからさ
32
大体 こういった問題は
平行四辺形に なるんじゃないか
そこで
対辺に 着目して
ベクトルの 引き算で
対辺を 出してくるでしょ
33
条件式が あるから
34
条件式を 変形してくと
ほら
出てきたでしょ
35
だからさ
平行四辺形だよ
お疲れ様です。