スローライフの森　数１　＆　自家菜園

01

図形とベクトル

計算の　形

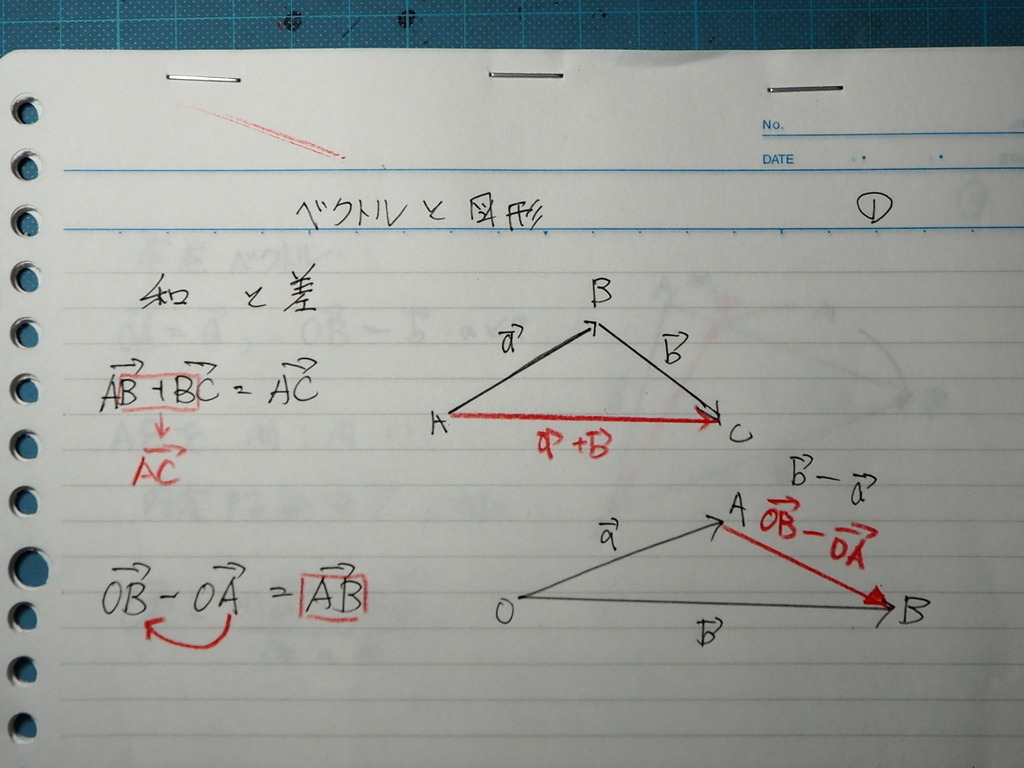
和　は　

ひっつ目のベクトルの　終点から　

次の　ベクトルを　書く

かんじに



差　は　　

始点の　おなじ　二つのベクトルの

先に　橋　を渡す感じで

方向は　差の式の

後ろから　前の様に

02

ベクトルの　大きさは

√（ｘ成分の二乗　+　y成分の二乗　）

ふつうの　ベクトル　位置ベクトル　のとき




成分を　引き算して　

ベクトルを　求めたときも

その　成分に関して

√（ｘ成分の二乗　+　y成分の二乗　）



03

分点ベクトル

公式は　これです

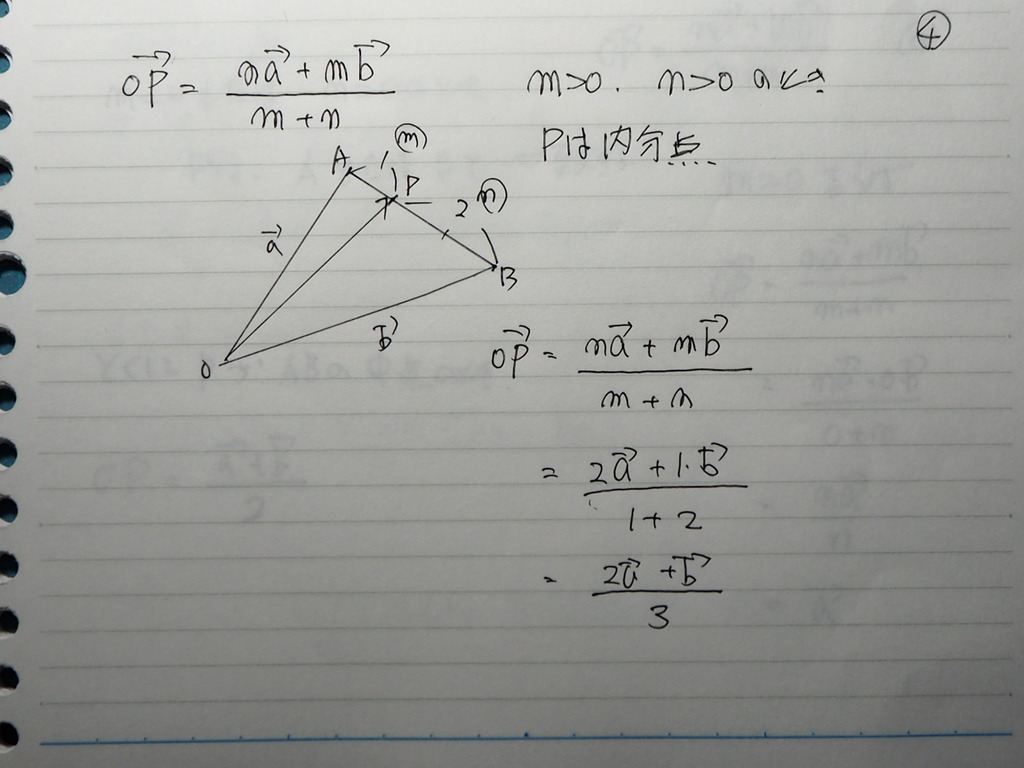
04

ｍ＞０　、ｎ＞０　の時は

内分点


分母は　ｍ+ｎ


分子は　それぞれの　ベクトルに

遠い方　を　掛ける



ｍ、ｎ　が　異符号の時

どっちかが　マイナスになるときは

マイナス側が

AB　の　外に来て


外分になる

06

ｍ、または　ｎ、が　＝０の時は

分点は　A　または　B　に　一致する



OPが　中点の時は

2分の　a+b

07

三角形　ABC　で　重心を　Gとすると


点O　を　それ以外の　どこかにとって


位置ベクトルで表すとき


OGベクトルは　1/3（　a+b+c）


08
平行の　条件は

0でない　実数倍で　表現できること

09

垂直条件


ベクトルは　成分で書かれてますが


垂直を　判別するのは　成分の

計算で


10
共線条件

３点が　一直線上にあるとき

始点を　合わせて

実数倍　表示ができること




11


実数倍が　負になるときは

始点を　合わせると

3 点　A,B,C　があるとき

Aにたいして　B、　C　は　

反対側　どうしになる

12
共線条件

位置ベクトルを　使って


直線　L、M　　の　交点　P


直線　M、N　　の　交点　Q


の　位置ベクトル

OP　=　OQ

を　示す

13

これらを　踏まえまして

問題




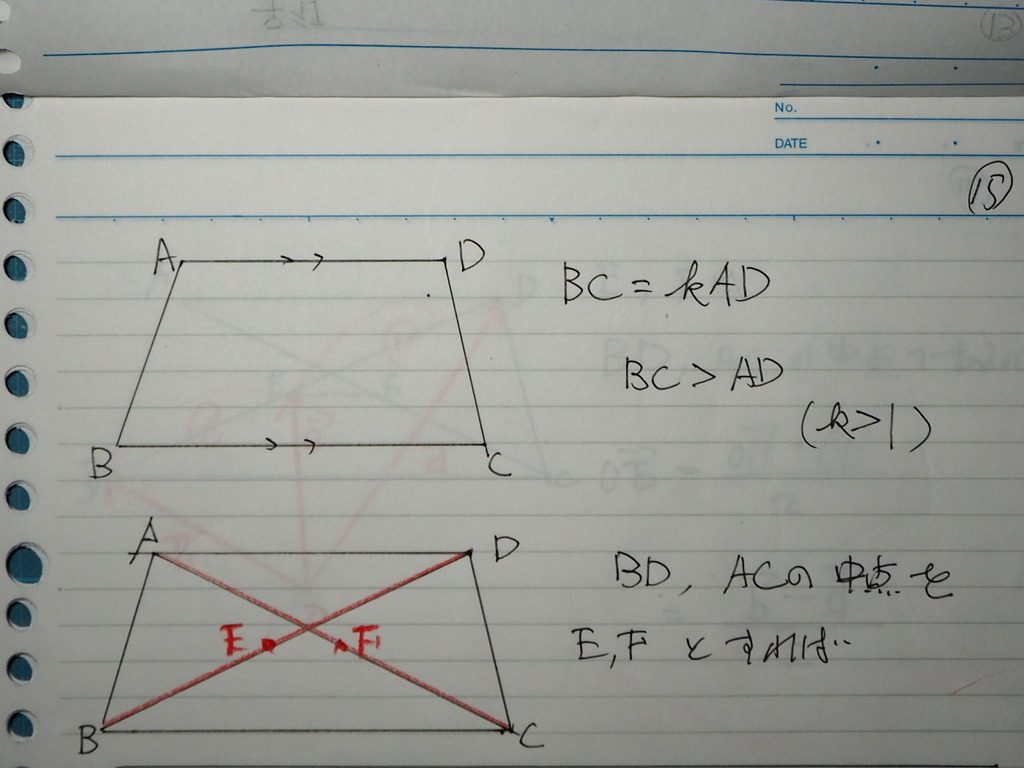
ある　台形　ABCD　があって

（　条件があります　

　　BC　平行　AD

　　BC　＞　AD　　　）




対角線の　中点を　E、F

とすれば

次のことが　成り立つことを

証明しなさい


という問題




14

まず　平行条件

平行なので

始点が　一緒では　ないですが

実数倍表示ができる

さらに

条件から

実数倍の　K　は

K　＞　１






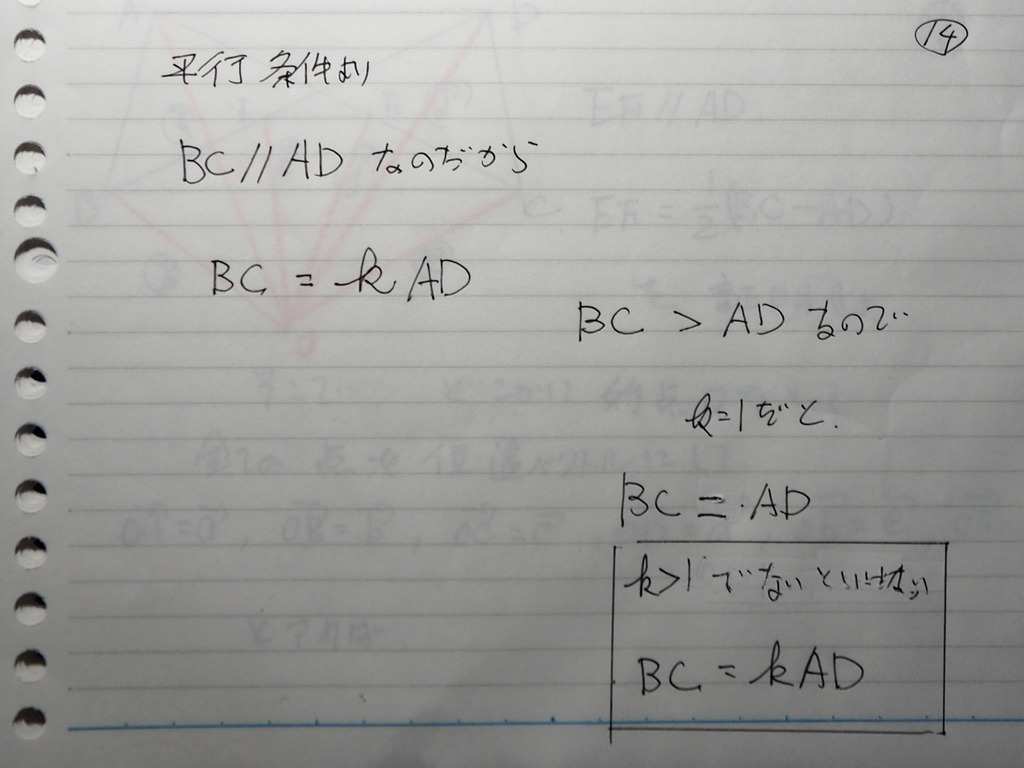
15

BD,　ACの　中点を　E,Fとするので

16

この時に

EF　平行　AD

EF　＝　1/2　（　BC　-　AD　）

を　証明せよ


そこで

これらの　外に　点O を　とって

位置ベクトルで

考えると


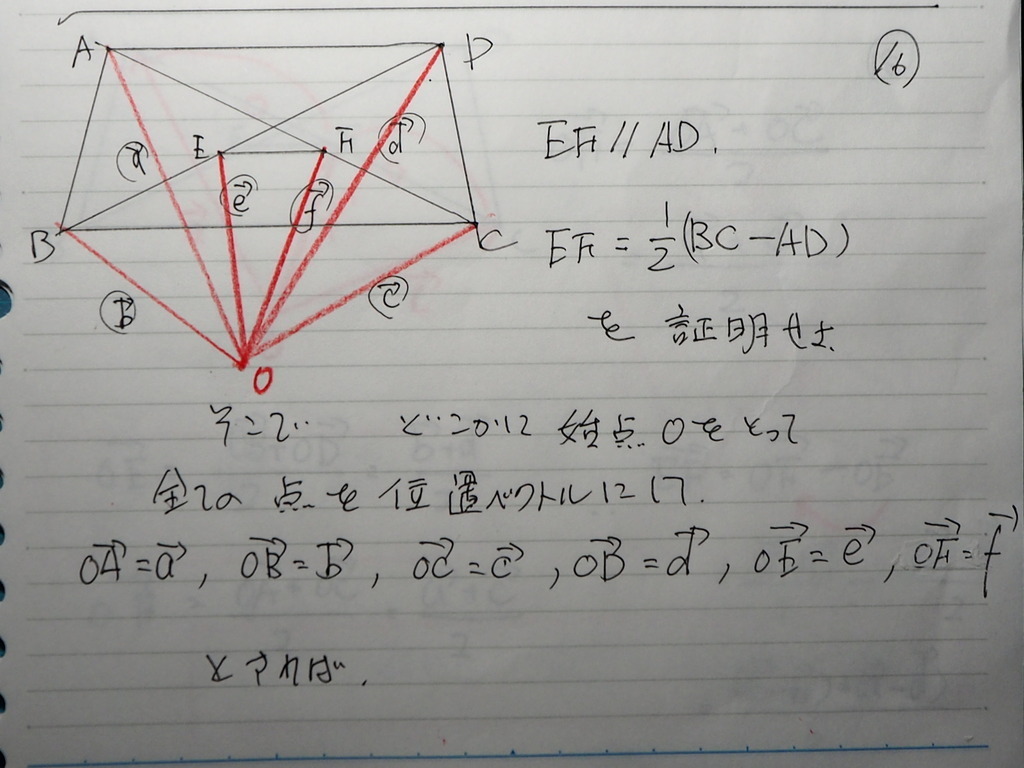
17

E,Fは　それぞれ

BD、AC　の　中点であるから

中点の　分点ベクトルで


OE　ベクトル

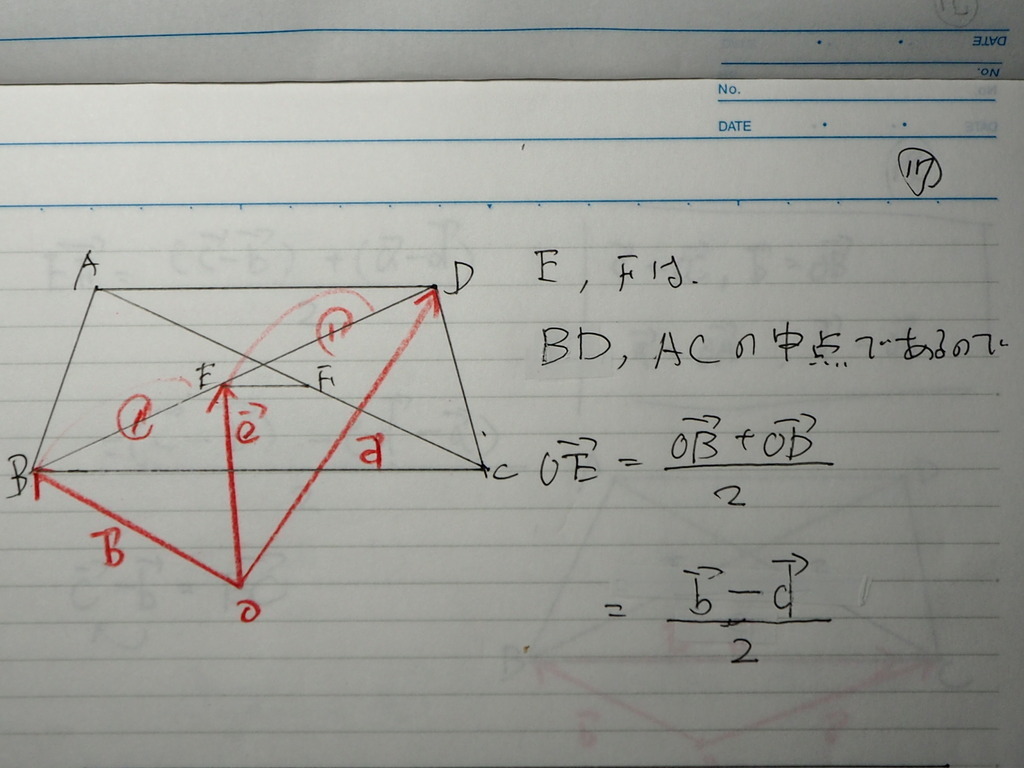
18


同じく

中点の　分点ベクトルで

OF


で　EF　ベクトルは　

OF-OE

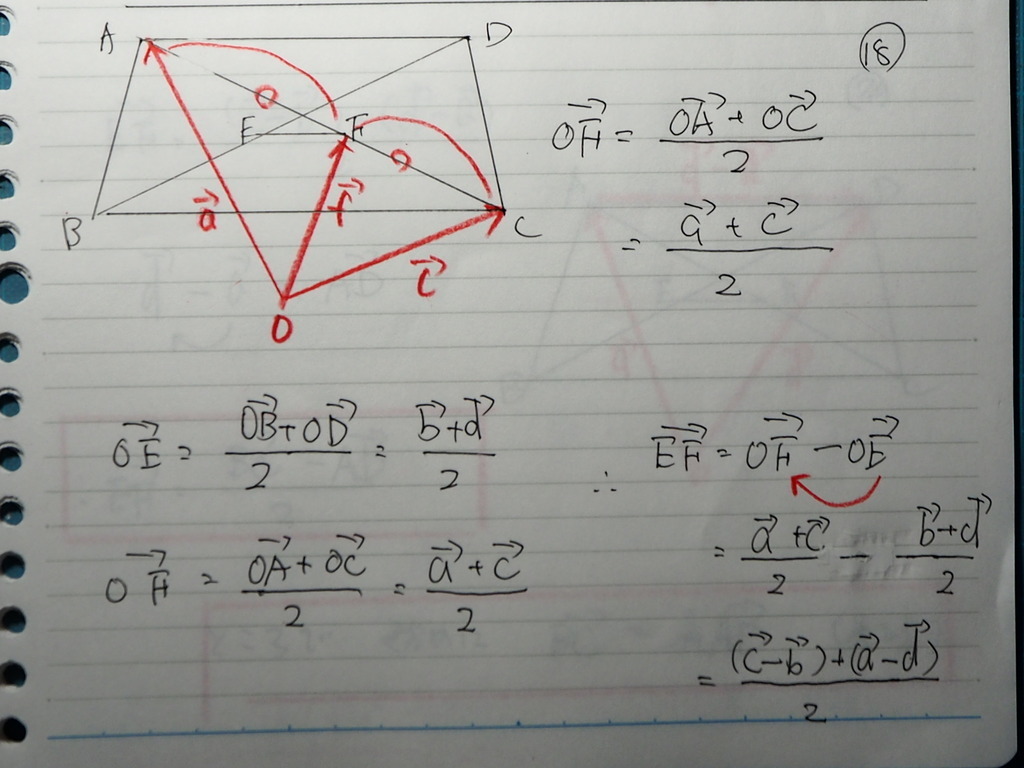
19
EF　ベクトルの　分点ベクトル表示で

分子の　左かっこは

BCベクトル

20
EF　ベクトルの　分点ベクトル表示で

分子の　右かっこは

ADベクトル



出てきた式に　


始めの　平行条件を代入したら


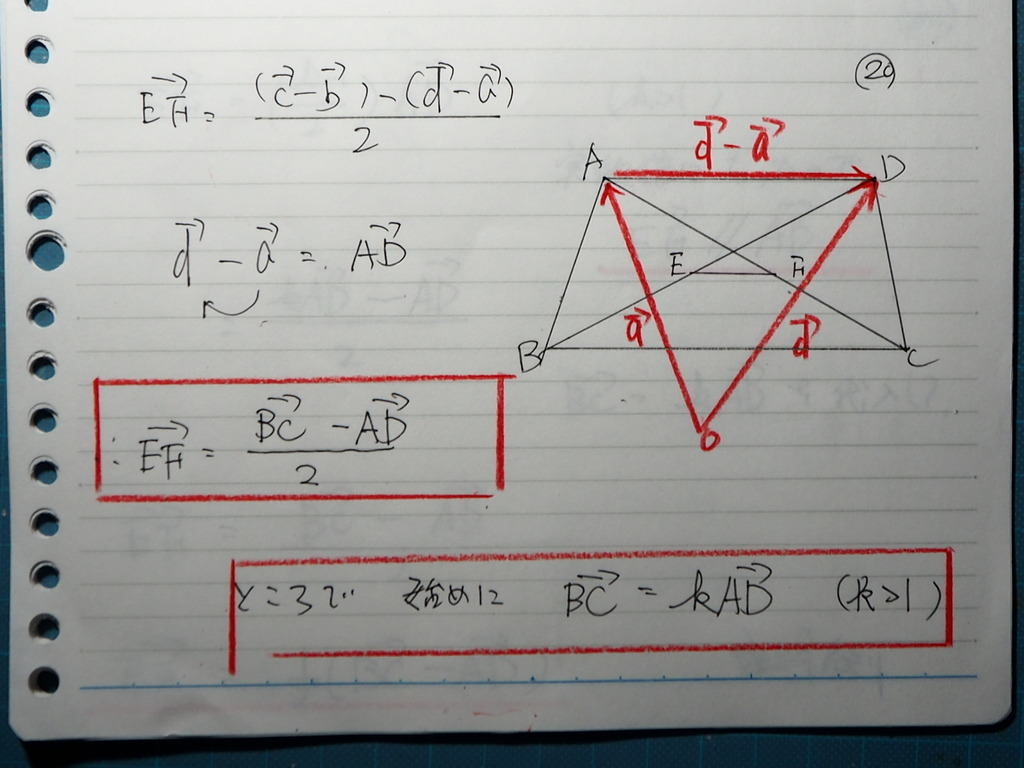
21

すでに　ここで　答えが　出てるんですが


先に　平行であることを

言いたいので

式変形して


22

EFと　ADが

実数倍表示が　できたので

EF　平行　AD

そして

少し　前に戻る感じで

BC＝K　AD　を　代入して

EF＝1/2（BC-AD)


23

次は

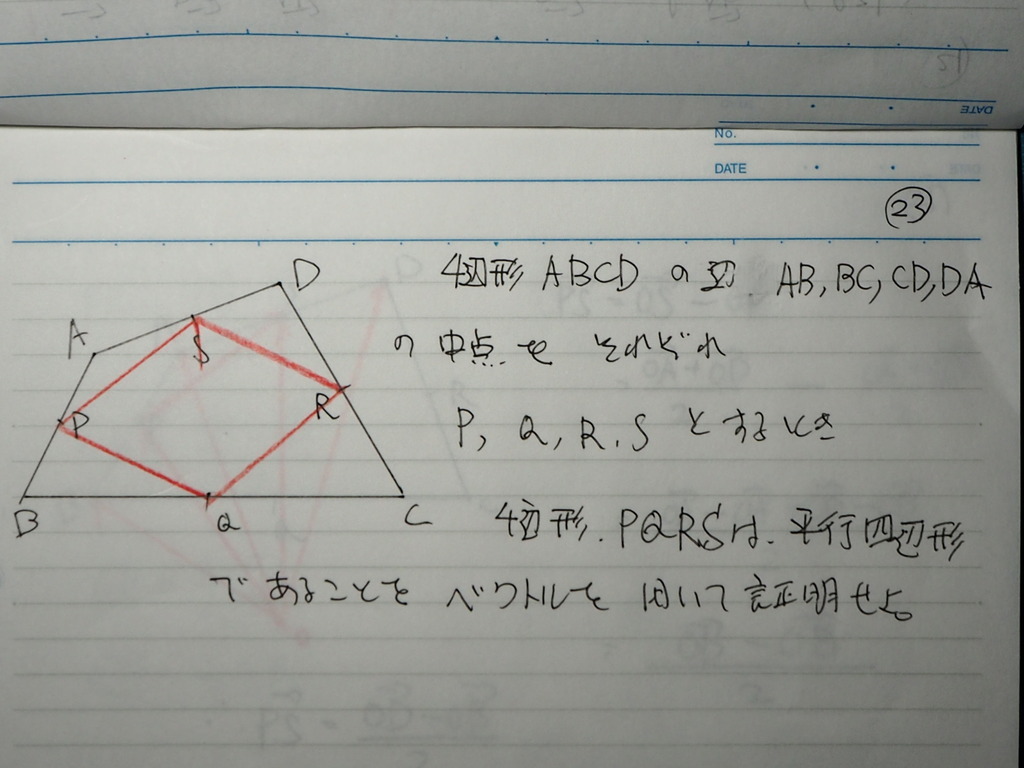
4辺形　ABCD　が　あるんだけども

それぞれ　AB,BC,CD,DA　の　中点を

P,Q,R,S　とすると


4辺形PQRSは　平行四辺形　であることを

証明しなさい　と言う　問題


24
なんだ　こりゃ

自分で書いたのに

読めない


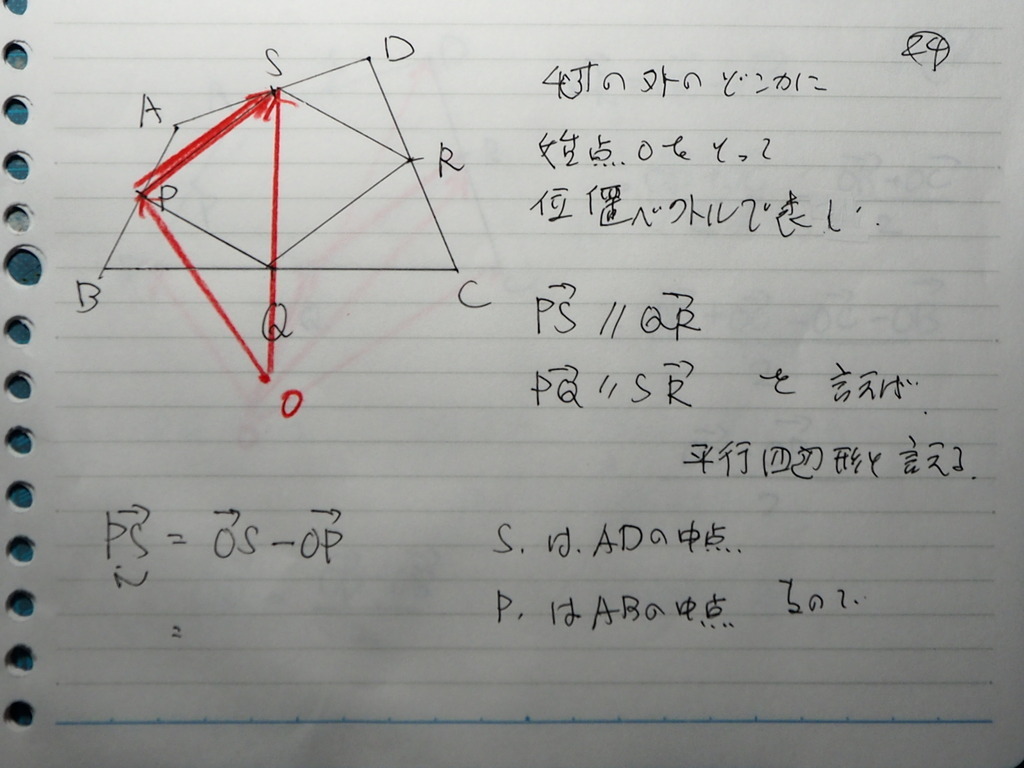
要するにですね

ABCDPQRS　いがいの　どこかに

点O　を　とって

位置ベクトルで

考えると


対辺が　平行であること

言えばいいんだから


（　平行で　大きさが　おなじ　）

25

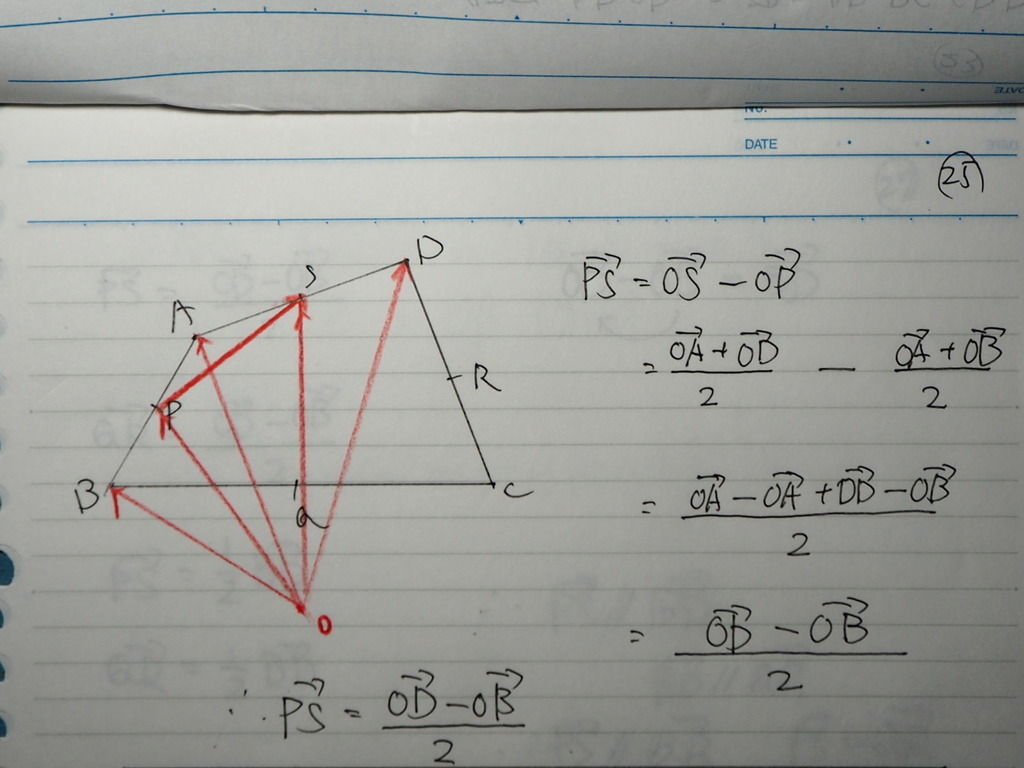
対辺を　調べてくでしょ

PS　と　QR

まず　PS　から

26

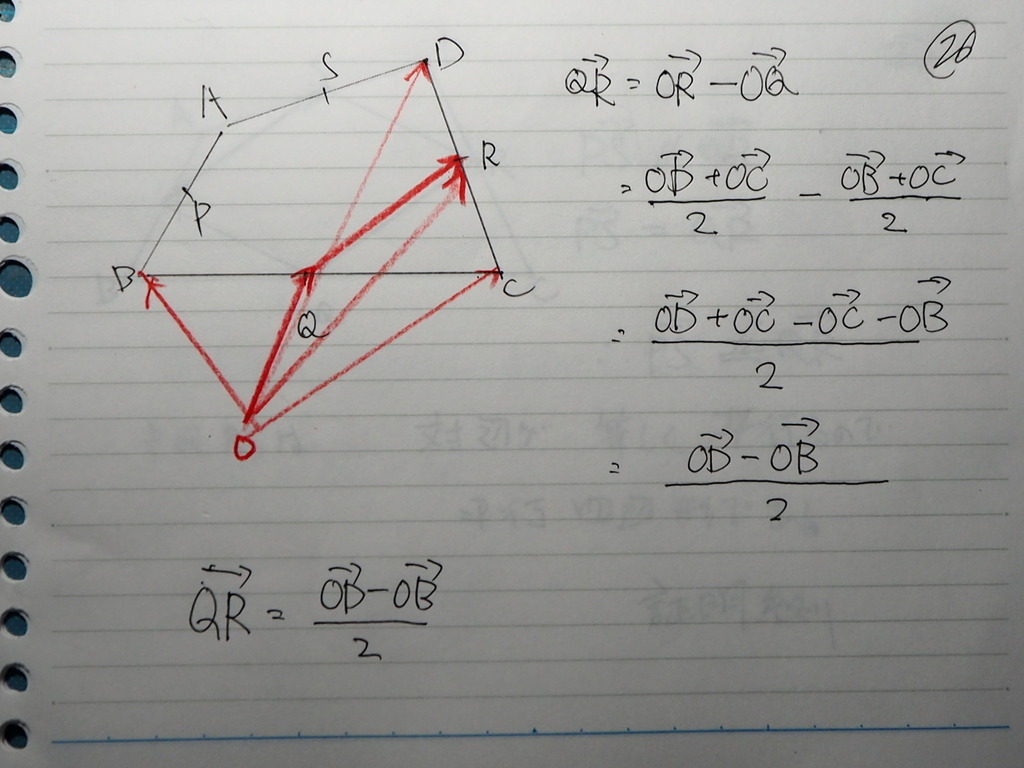
QRは

おなじだ

27


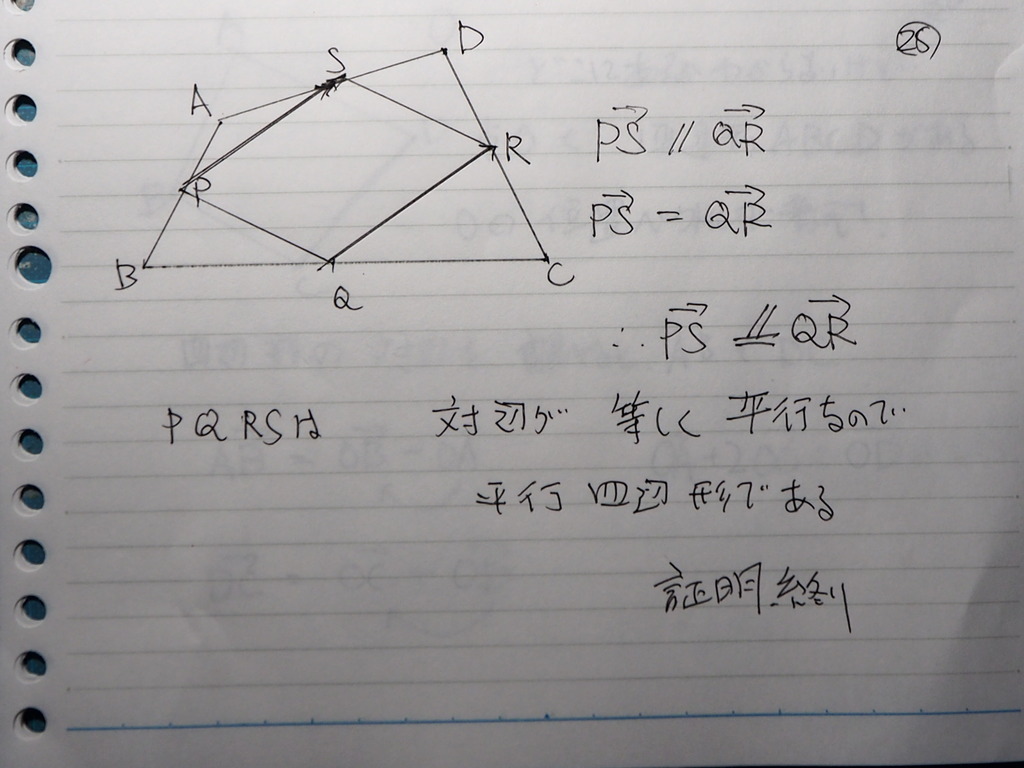
というわけで

PS　平行　QR

PS =　QR

（　ベクトルは　平行移動できる　）


28

PQRSは　平行四辺形

29

4辺形　ABCD　と　1点　O　があって

OA　+　２OC　=　OD　+　２OB


である　この4辺形の　形状は何？

30

対辺を　調べればさ

AB　と　DC


条件は　これだから

んん〜

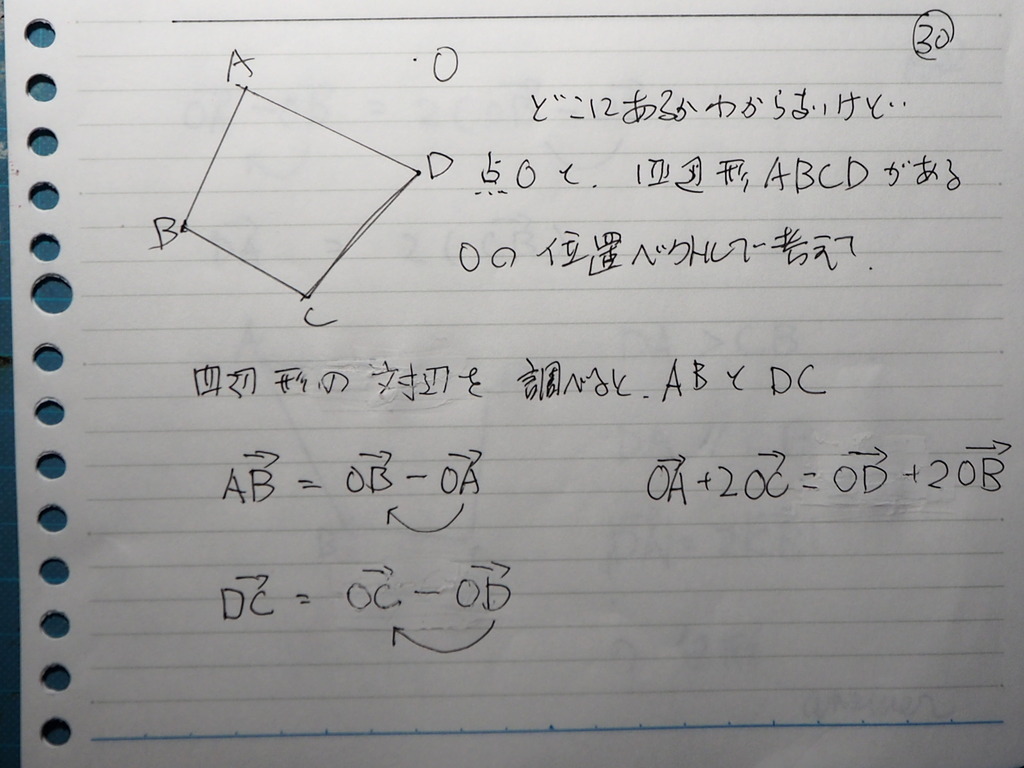
31

条件式の方から

対辺を　出してきた方がいいから

やっぱりさ


対辺を　AD　と　BC　にして

考えると


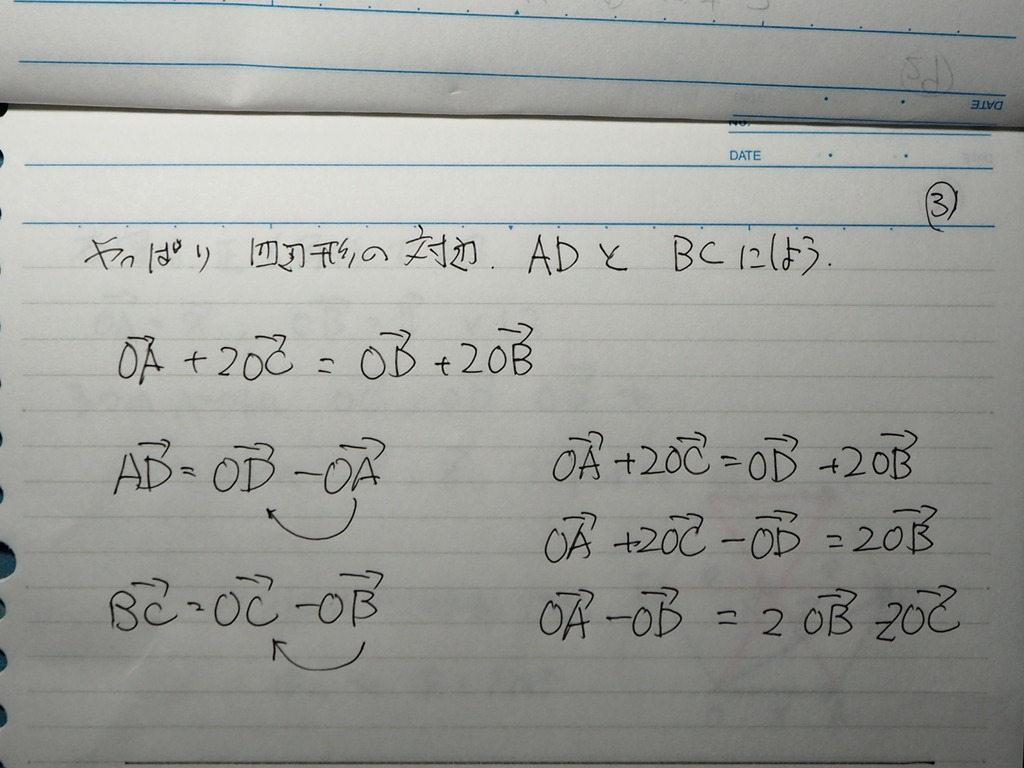
32

条件式を　変形して

対辺を　作ってくと

対辺が　実数倍　

対辺が　平行で

大きさが　ADが　BCの　2倍

な　　台形　だね

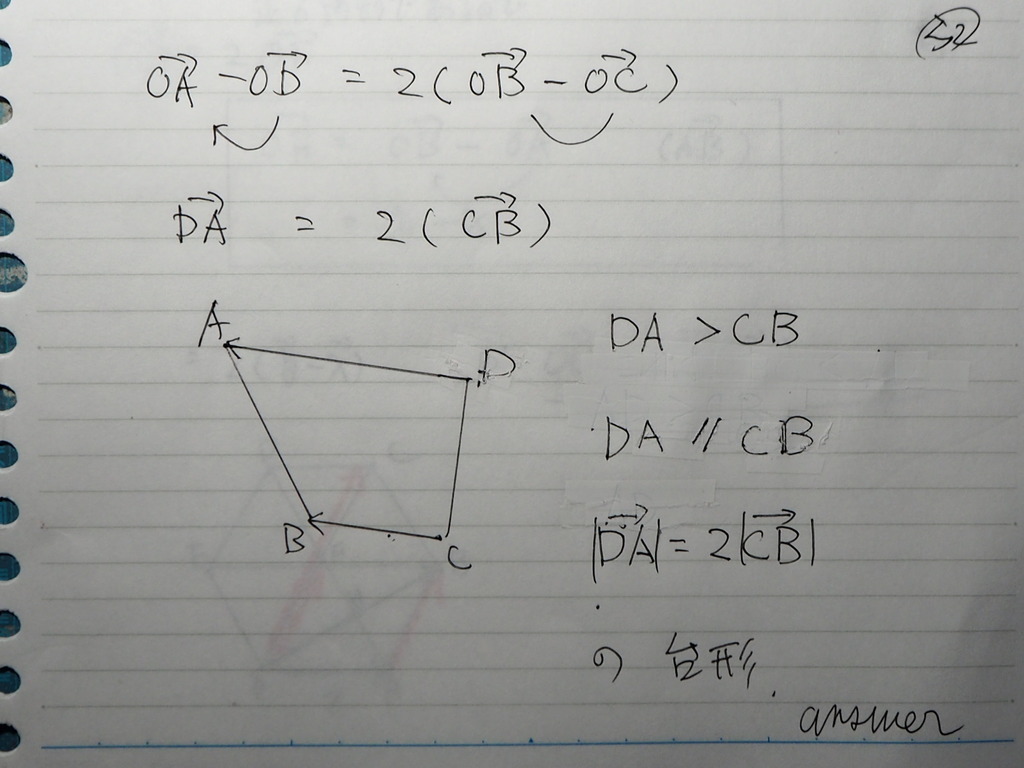
33
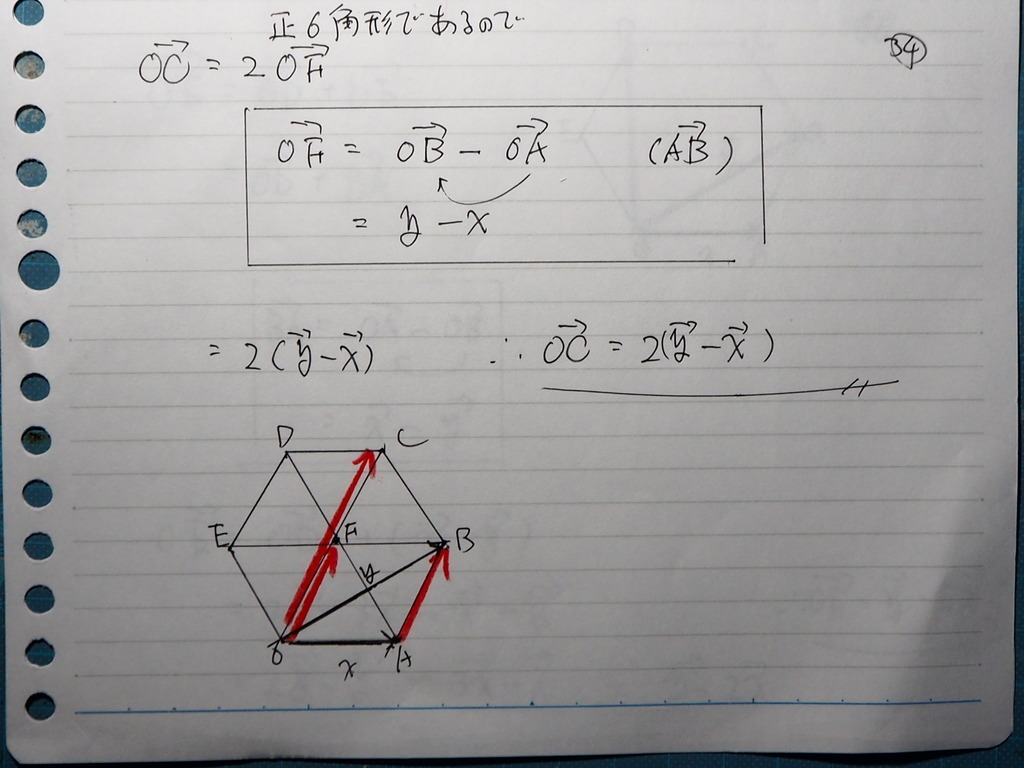
正6角形がありました

OABCDE　です

OA=xベクトル

OB=ｙベクトル

とするときに

OC,OD,OE　ベクトルの

成分を　ｘ、ｙで表せ

34

やり方は　いろいろ　あります

正六角形であることと

ベクトルは　平行移動できること

ベクトルには　向きがあることを

使って

35

答えは　一つですが

やり方は　いろいろあるため

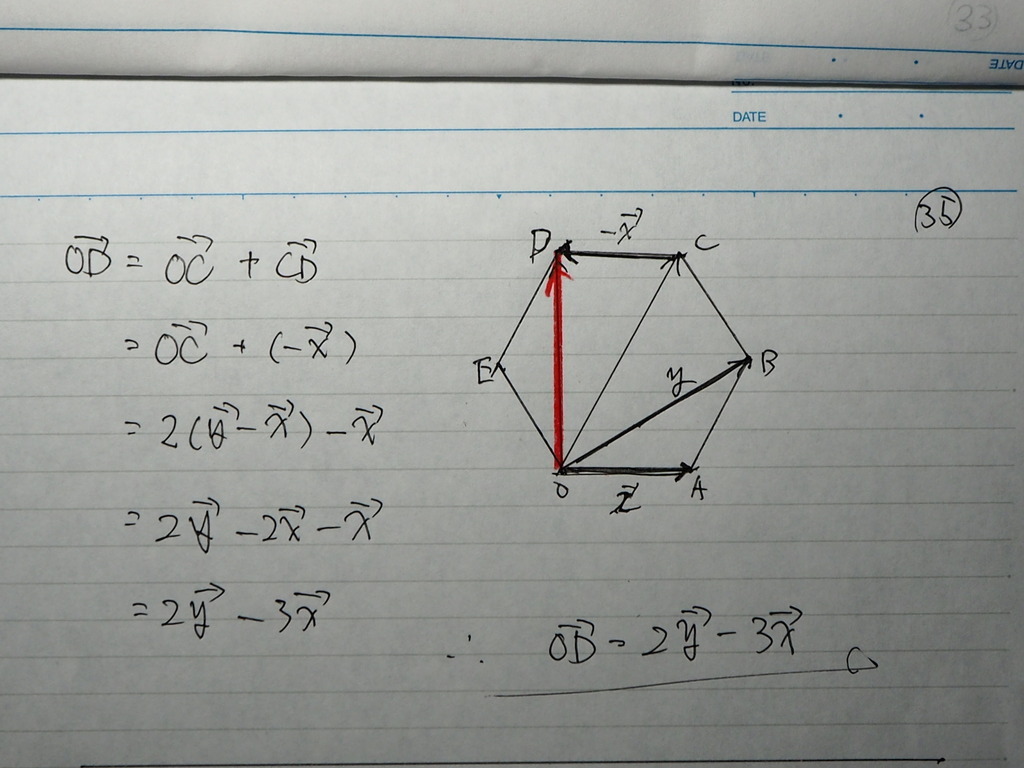
36

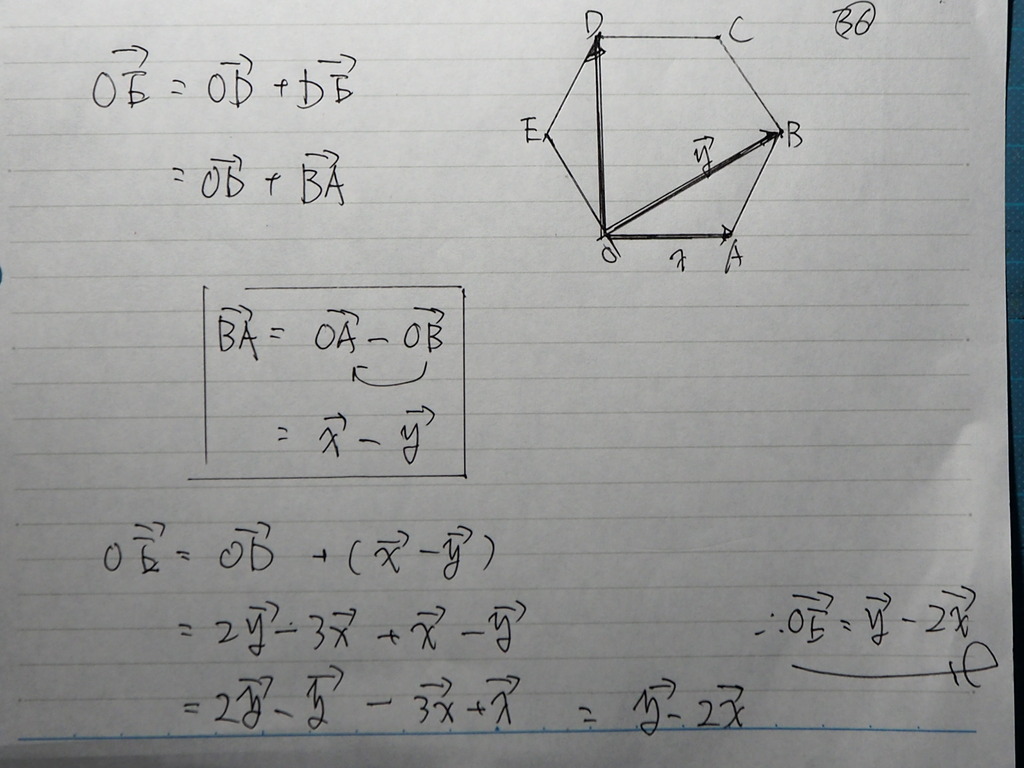
こんな感じに　しましたが


答えは　あってるって




お疲れ様です。