�V�K�L���̓��e���s�����ƂŁA��\���ɂ��邱�Ƃ��\�ł��B
�L��
�V�K�L���̓��e���s�����ƂŁA��\���ɂ��邱�Ƃ��\�ł��B
posted by fanblog
2020�N09��05��
�͂��������A�˂͐L�т�I
����ɂ��́AYOSHIO�ł��B
����͗͂̂V��ځA�t�b�N�̖@���ł��B
�͂̑傫���ɂ˂��ւ��������̌v�Z�ł��B
�Ƃɂ����v�Z�͌��̗͂��āA�ǂݐi�߂Ă݂Ă��������ˁB
�c�ߋ��ɁA�m�����疭�Ȏ���������Ƃ����x������܂��B
�u�搶�A�ǂ����Ă˂̒������v�Z���悤�Ƃ����́H�v
�c�����A����Ȃ��ƕ�����Ȃ��ł��c�B
�������A�����������܂���c�B
����ǁA���̂悤�Ȏ���E�^��������Ă��邱�Ƃ��A��������ł���ˁB
�����ł����Ȃɋ����������Ă��炦�Ă���C������̂ŁB
����ł́A����̃e�[�}�ł����t�b�N�̖@���Ƃ́A
�˂̂̂т��A�������͂̑傫���ɔ�Ⴗ�鐫�����w���܂��B
���͂ɂ���ʂ�A�˂̂̂тƗ͂̑傫�����������OK�ł��B
���ۂ̊�{���́A���̂悤�ɏo�肳��܂��B
��j���̃O���t�̂悤�ɁA�˂P�Ƃ˂Q���ꂼ��ɗ͂�����������
�˂��L�т������������Ă���B
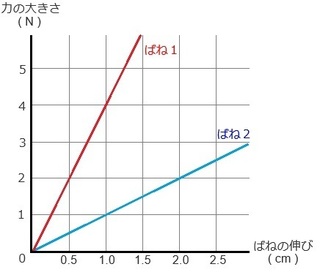
(1) �͂̑傫���Ƃ˂̐L�тɂ͂ǂ̂悤�ȊW�����邩�B
(2) (1)���番���鐫�������Ƃ������B
(3) �˂P�ɂU N �̗͂���������A�˂͉� cm �L�т邩�B
(4) �˂Q���P�O cm �L�т����A�� N �̗͂������������B
(1) �͂̑傫���Ƃ˂̐L�т̊W�́A
�@���W�ł��B
�@�����A�u���W��������Ȃ��c�v�Ƃ����ꍇ�́A
�@���₭�������đ��v�ł�����ˁB
�@���肪�������ƂɁA���̗͂̑傫���Ƃ˂̐L�т̊W�́A
�@���W�����o�Ă��܂���B
�@�ň��A���W�Ƃ������t��m���Ă��������ł�OK�ł��B
(2) �͂̑傫���Ƃ˂̐L�т̊W����킩�鐫���́A �t�b�N�̖@���ł��B
�@�]�k�ł����A���炭�O�܂ł��u�ǂ�Ȗ@�����H�v��
�@�o�肳��邱�Ƃ����������ł����A
�@�ŋ߂ł��u�ǂ�Ȑ������H�v�Ƃ����o��������Ă��܂��B
�@���t�ɘf�킳��Ȃ��悤�ɒ��ӂ��Ă݂Ă��������ˁB
�ł́A��������́A�v�Z�ł��ˁB������x�����m�F�ł��B
(3) �˂P�ɂU N �̗͂���������A�˂͉� cm �L�т邩�B
(4) �˂Q���P�O cm �L�т����A�� N �̗͂������������B
�c���肪�������ƂɁI
�O���t�ŏo�����ꂽ��A���ʂȌv�Z�����͕K�v����܂���I
���w�ŏK���܂����A��Ꭾ���g���ĉ����܂��B
(3) �˂P�̃O���t�����Ă݂܂��傤�B
�@�܂��́A�O���t�ŕ�����₷���_���P���������܂��B
�@�˂̐L�т��O�D�T cm �̎��A�͂̑傫�����QN �ł���ˁB
�@���̐��l���g���āA�O�D�Tcm�F�QN�@�Ŕ�̎������܂��B
�@���ɁA��肩���UN �̎��̂˂̐L�т����߂�̂ŁA
�@���߂���̂� X (cm) �Ƃ���ƁAX cm�F�UN�@�œ����悤�Ɏ������܂��B
�@�����āA��ꂽ�Q�̔�̎����u���v�łȂ��܂��B
�@�@�O�D�Tcm�F�QN �� X cm�F�UN
�@���̎��������A�����P�D�Tcm �Ƌ��߂��܂��B
���߂āA(3)�����ɃO���t���g�����t�b�N�̖@�����̉������́A
�@ �O���t���琔�l��������P�_���g���Ĕ�̎������
�A ��肩�狁�߂���̂��Œu���Ĕ�̎������
�B �@���A�̔�Ꭾ������ĉ���
�� ��̎��́A�P�ʂ̏��Ԃ����낦���悤�ɂ��܂��傤�B
���s���Ă��ǂ��̂ŁA�`�������W���邱�ƂŊ��o�����߂Ă��܂�����ˁB
�ł́A�Ō��(4)����L�̉������ʼn����܂��B
�@ �O���t���琔�l��������P�_���g���Ĕ�̎������
�@�˂̂̂т��P�D�Ocm �̎��ɁA�͂̑傫�����PN �Ȃ̂ŁA
�@�@�@�P�D�Ocm�F�PN�@�Ŕ�̎��ł��B
�A ��肩�狁�߂���̂��Œu���Ĕ�̎������
�@��肩��A�˂̐L�т��P�O cm�̎��̗͂̑傫���Ȃ̂ŁA
�@���߂���̂� Y (N) �Ƃ���ƁA�@
�@�@�@�P�Ocm�FY N�@�Ŕ�̎��ł��B
�@
�B �@���A�̔�Ꭾ������ĉ���
�@�@�@�P�D�Ocm�F�PN �� �P�Ocm�FY N
�@���̔�Ꭾ�������āA�����͂P�ON�@�ł��ˁB
�ł́A����̃t�b�N�̖@���ɂ��Ă͂R�̃|�C���g�B
�@ �t�b�N�̖@���́A�˂̐L�тƗ͂̑傫�������W
�A �v�Z������Ꭾ������čU��
�B ��̎�����鎞�́A�P�ʂ̏��Ԃ����낦��
���͖��ɃO���t�����邾���Őg�\���܂����A
�O���t���v�Z�������T�|�[�g�L����
�݂����Ȋ����Ŏv����悤�ɂȂ�ƁA�C�����y�ɂȂ��Ă��܂�����ˁB
����ŗ́E���͍͂Ō�Ȃ̂ŁA
�����ЂƓ���A���Ə����A�撣���Ă݂܂��H
�� �Ō�܂œǂ�Œ����Ă��肪�Ƃ��������܂����I
���̃u���O���ɂ�����܂������A
�u��Ꭾ�v���u�O���t�̌����v���A
������Ȃ����Ƃ�����A�R�����g�ŋL�����Ē����܂�����A
�u���O�ʼn��߂Đ�����������肽���Ǝv���܂��B
����͗͂̂V��ځA�t�b�N�̖@���ł��B
�͂̑傫���ɂ˂��ւ��������̌v�Z�ł��B
�Ƃɂ����v�Z�͌��̗͂��āA�ǂݐi�߂Ă݂Ă��������ˁB
�c�ߋ��ɁA�m�����疭�Ȏ���������Ƃ����x������܂��B
�u�搶�A�ǂ����Ă˂̒������v�Z���悤�Ƃ����́H�v
�c�����A����Ȃ��ƕ�����Ȃ��ł��c�B
�������A�����������܂���c�B
����ǁA���̂悤�Ȏ���E�^��������Ă��邱�Ƃ��A��������ł���ˁB
�����ł����Ȃɋ����������Ă��炦�Ă���C������̂ŁB
����ł́A����̃e�[�}�ł����t�b�N�̖@���Ƃ́A
�˂̂̂т��A�������͂̑傫���ɔ�Ⴗ�鐫�����w���܂��B
���͂ɂ���ʂ�A�˂̂̂тƗ͂̑傫�����������OK�ł��B
���ۂ̊�{���́A���̂悤�ɏo�肳��܂��B
��j���̃O���t�̂悤�ɁA�˂P�Ƃ˂Q���ꂼ��ɗ͂�����������
�˂��L�т������������Ă���B

(1) �͂̑傫���Ƃ˂̐L�тɂ͂ǂ̂悤�ȊW�����邩�B
(2) (1)���番���鐫�������Ƃ������B
(3) �˂P�ɂU N �̗͂���������A�˂͉� cm �L�т邩�B
(4) �˂Q���P�O cm �L�т����A�� N �̗͂������������B
(1) �͂̑傫���Ƃ˂̐L�т̊W�́A
�@���W�ł��B
�@�����A�u���W��������Ȃ��c�v�Ƃ����ꍇ�́A
�@���₭�������đ��v�ł�����ˁB
�@���肪�������ƂɁA���̗͂̑傫���Ƃ˂̐L�т̊W�́A
�@���W�����o�Ă��܂���B
�@�ň��A���W�Ƃ������t��m���Ă��������ł�OK�ł��B
(2) �͂̑傫���Ƃ˂̐L�т̊W����킩�鐫���́A �t�b�N�̖@���ł��B
�@�]�k�ł����A���炭�O�܂ł��u�ǂ�Ȗ@�����H�v��
�@�o�肳��邱�Ƃ����������ł����A
�@�ŋ߂ł��u�ǂ�Ȑ������H�v�Ƃ����o��������Ă��܂��B
�@���t�ɘf�킳��Ȃ��悤�ɒ��ӂ��Ă݂Ă��������ˁB
�ł́A��������́A�v�Z�ł��ˁB������x�����m�F�ł��B
(3) �˂P�ɂU N �̗͂���������A�˂͉� cm �L�т邩�B
(4) �˂Q���P�O cm �L�т����A�� N �̗͂������������B
�c���肪�������ƂɁI
�O���t�ŏo�����ꂽ��A���ʂȌv�Z�����͕K�v����܂���I
���w�ŏK���܂����A��Ꭾ���g���ĉ����܂��B
(3) �˂P�̃O���t�����Ă݂܂��傤�B
�@�܂��́A�O���t�ŕ�����₷���_���P���������܂��B
�@�˂̐L�т��O�D�T cm �̎��A�͂̑傫�����QN �ł���ˁB
�@���̐��l���g���āA�O�D�Tcm�F�QN�@�Ŕ�̎������܂��B
�@���ɁA��肩���UN �̎��̂˂̐L�т����߂�̂ŁA
�@���߂���̂� X (cm) �Ƃ���ƁAX cm�F�UN�@�œ����悤�Ɏ������܂��B
�@�����āA��ꂽ�Q�̔�̎����u���v�łȂ��܂��B
�@�@�O�D�Tcm�F�QN �� X cm�F�UN
�@���̎��������A�����P�D�Tcm �Ƌ��߂��܂��B
���߂āA(3)�����ɃO���t���g�����t�b�N�̖@�����̉������́A
�@ �O���t���琔�l��������P�_���g���Ĕ�̎������
�A ��肩�狁�߂���̂��Œu���Ĕ�̎������
�B �@���A�̔�Ꭾ������ĉ���
�� ��̎��́A�P�ʂ̏��Ԃ����낦���悤�ɂ��܂��傤�B
���s���Ă��ǂ��̂ŁA�`�������W���邱�ƂŊ��o�����߂Ă��܂�����ˁB
�ł́A�Ō��(4)����L�̉������ʼn����܂��B
�@ �O���t���琔�l��������P�_���g���Ĕ�̎������
�@�˂̂̂т��P�D�Ocm �̎��ɁA�͂̑傫�����PN �Ȃ̂ŁA
�@�@�@�P�D�Ocm�F�PN�@�Ŕ�̎��ł��B
�A ��肩�狁�߂���̂��Œu���Ĕ�̎������
�@��肩��A�˂̐L�т��P�O cm�̎��̗͂̑傫���Ȃ̂ŁA
�@���߂���̂� Y (N) �Ƃ���ƁA�@
�@�@�@�P�Ocm�FY N�@�Ŕ�̎��ł��B
�@
�B �@���A�̔�Ꭾ������ĉ���
�@�@�@�P�D�Ocm�F�PN �� �P�Ocm�FY N
�@���̔�Ꭾ�������āA�����͂P�ON�@�ł��ˁB
�ł́A����̃t�b�N�̖@���ɂ��Ă͂R�̃|�C���g�B
�@ �t�b�N�̖@���́A�˂̐L�тƗ͂̑傫�������W
�A �v�Z������Ꭾ������čU��
�B ��̎�����鎞�́A�P�ʂ̏��Ԃ����낦��
���͖��ɃO���t�����邾���Őg�\���܂����A
�O���t���v�Z�������T�|�[�g�L����
�݂����Ȋ����Ŏv����悤�ɂȂ�ƁA�C�����y�ɂȂ��Ă��܂�����ˁB
����ŗ́E���͍͂Ō�Ȃ̂ŁA
�����ЂƓ���A���Ə����A�撣���Ă݂܂��H
�� �Ō�܂œǂ�Œ����Ă��肪�Ƃ��������܂����I
���̃u���O���ɂ�����܂������A
�u��Ꭾ�v���u�O���t�̌����v���A
������Ȃ����Ƃ�����A�R�����g�ŋL�����Ē����܂�����A
�u���O�ʼn��߂Đ�����������肽���Ǝv���܂��B