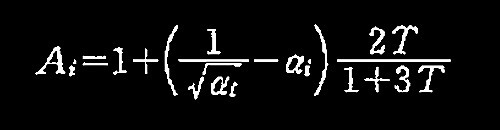(選択理由記述式4肢択ー問題)
No.1~No.10
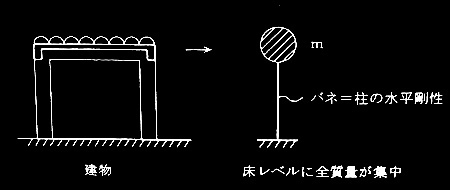
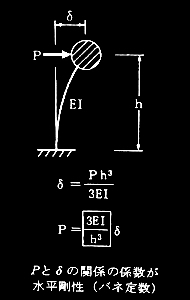
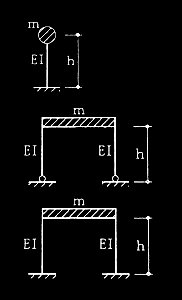
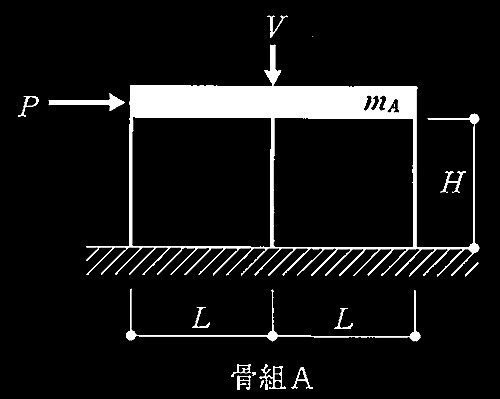
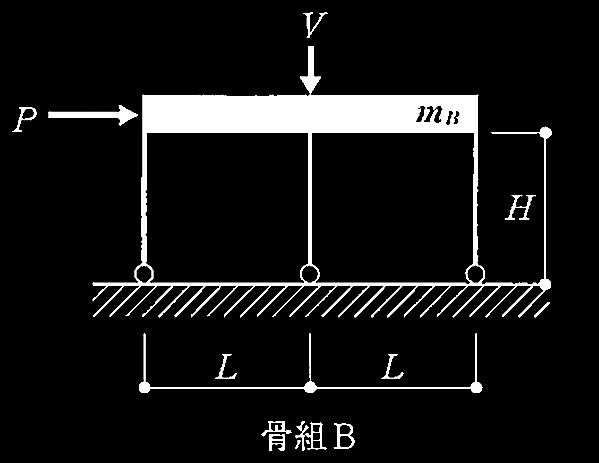
No.1 柱脚の固定条件が異なる2つの骨組の水平剛性の比
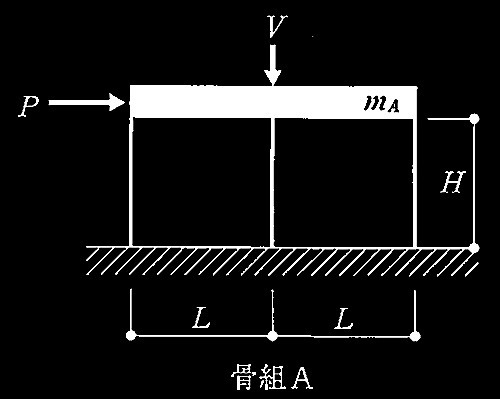
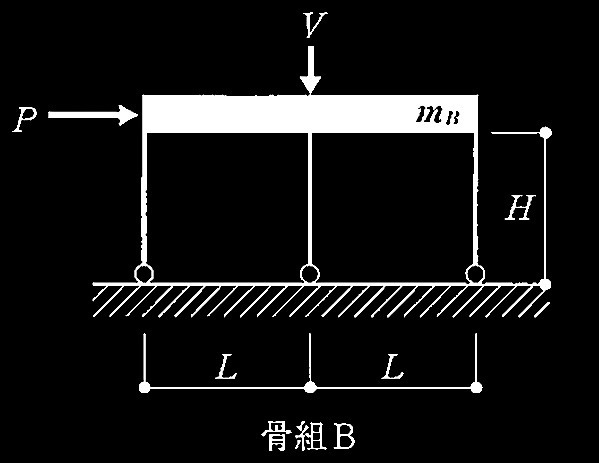
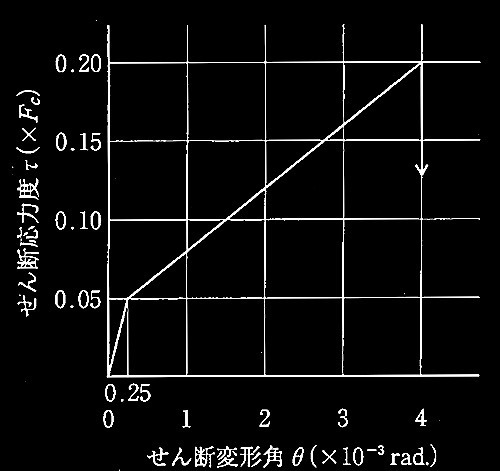
No.2 構造材料の応カ-ひずみ関係
No.3 構造計画・構造解析
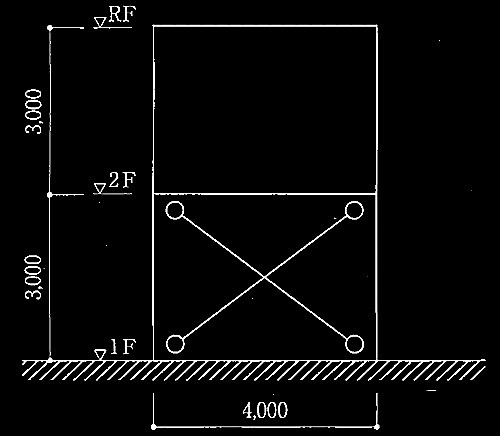
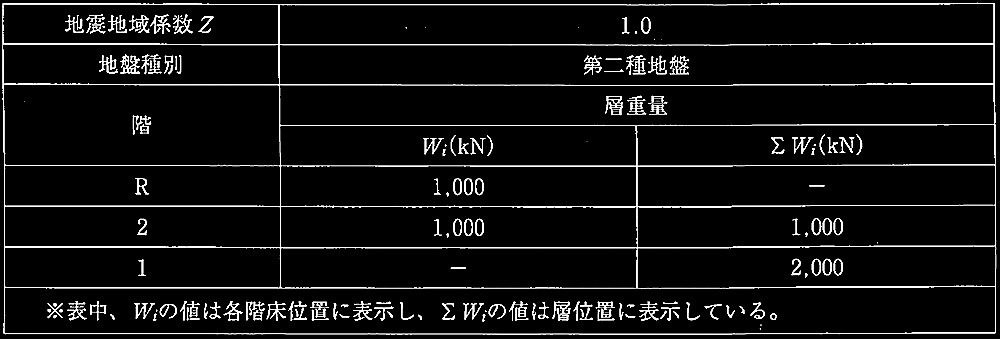
No.4 耐震設計
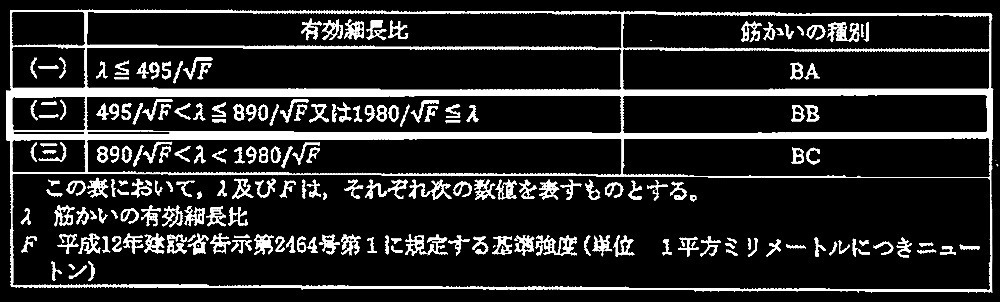
No.5 鉄骨構造
No.6 鉄筋コンクリート造の構造設計
No.7 木質構造等の構造設計
No.8 免震構造•制振構造
No.9 地盤•基礎
No.10 耐震診断•耐震補強
問題1
直接基礎(独立フーチング基礎)の設計
[ No.1 ]
硬質粘土地盤を支持層とする直接基礎
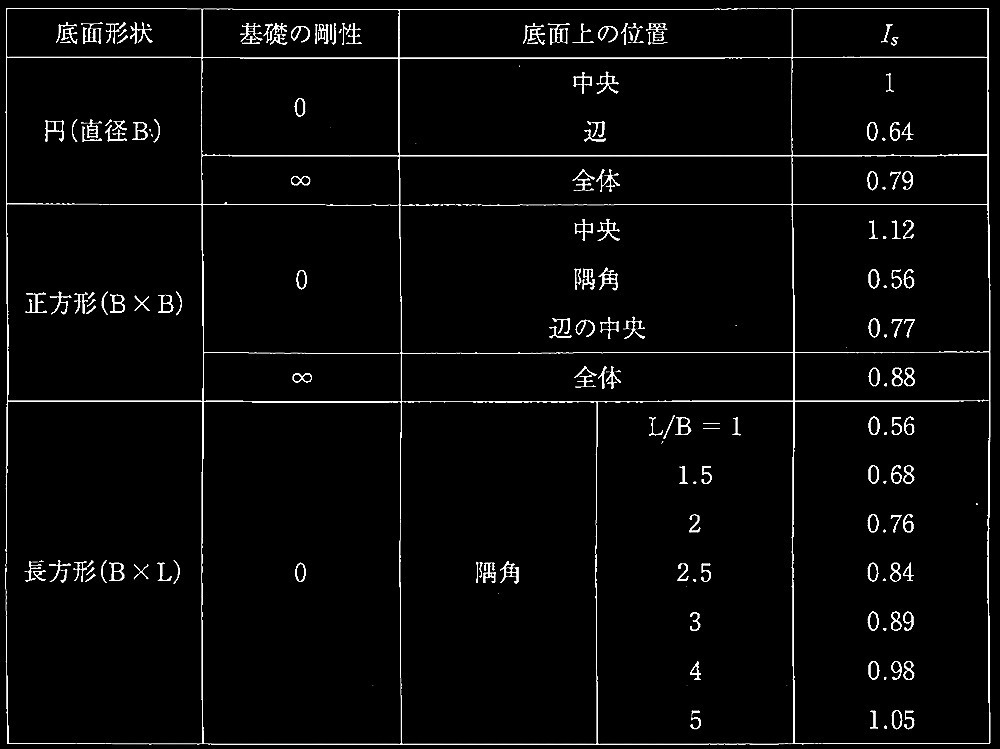
長期許容鉛直支持力及び即時沈下量の検討
① 地盤の長期許容鉛直支持力qαLを求める。
② 長期接地圧pを求める。
③ 長期許容鉛直支持力qαLと長期接地圧Pの比較により、
支持地盤の安全性を検証する。
④ 検討の対象とする独立フーチング基礎の即時沈下量SEを求める。
⑤ 独立フーチング基礎に対する安全性を検証する。
[ No.2 ]
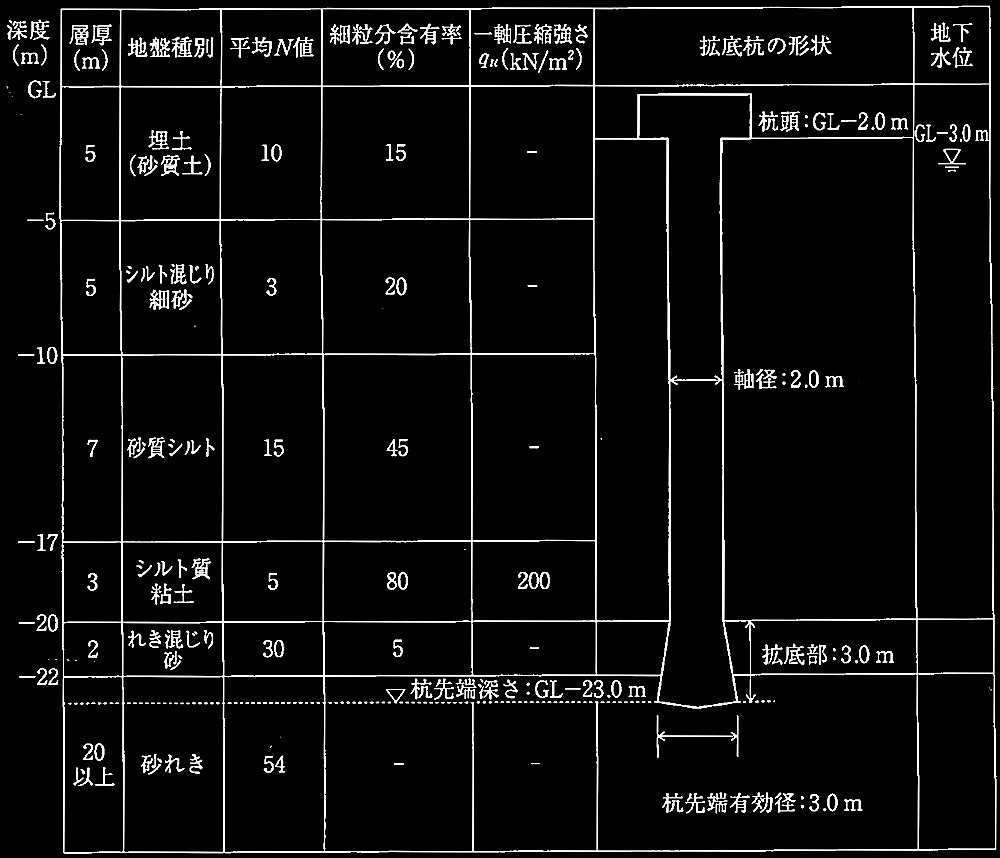
場所打ち鉄筋コンクリート拡底杭(軸径2.0m、杭先端有効径3.0m)
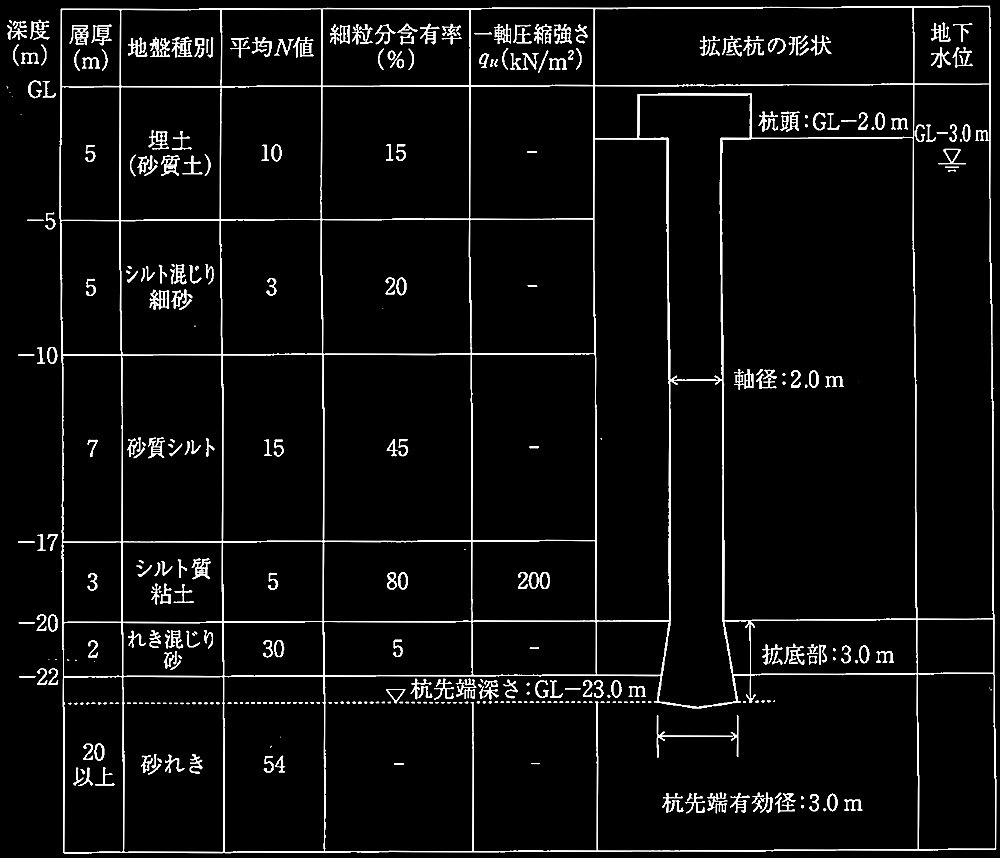
① 杭の極限先端抵抗力Rpを求める。
② 液状化の検討を必要とするすべての地盤種別を挙げ、その理由を3つ述べる。
③ 液状化の可能性が高い砂質シルト土層の極限周面摩擦抵抗力Rfsを求める。
④ 当該地盤におけるシルト質粘土層の極限周面摩擦抵抗力Rfcを求める。
⑤ 杭の長期許容鉛直支持力RαLを求めよ。
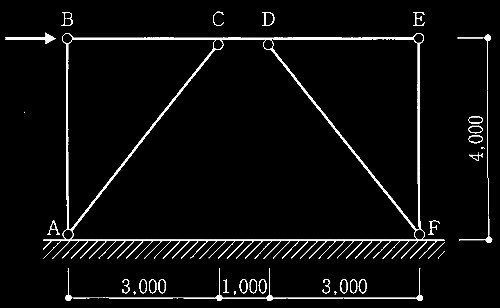
問題2
偏心K形筋かい付き鉄骨架構の柱頭部
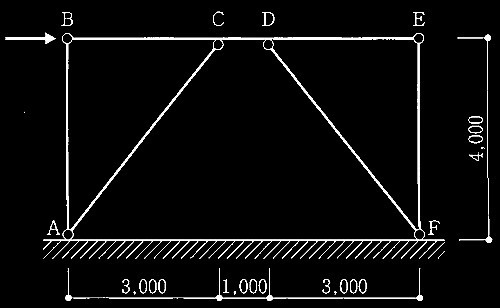
[ No.1 ]
梁の全塑性モーメントMpを求める
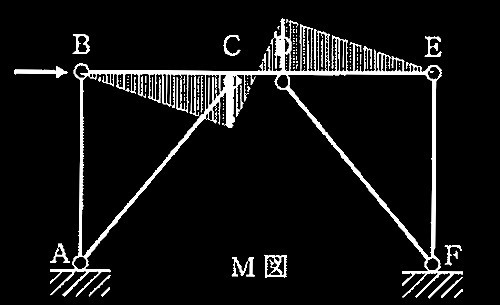
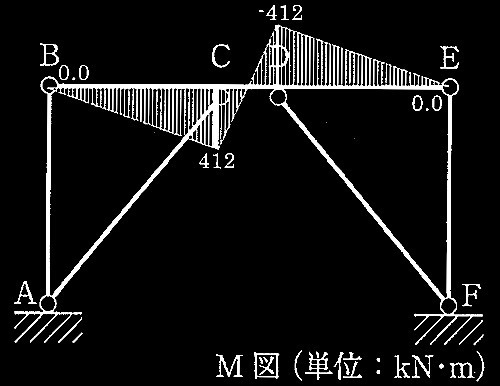
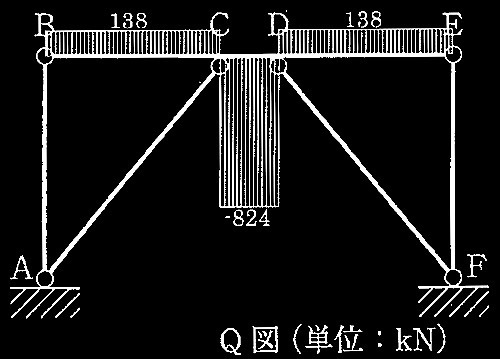
[ No.2 ]
モーメント図及びせん断力図を描く
筋かいACと筋かいDFは座屈拘束ブレース(軸降伏耐力 1,200 kN)
[ No.3 ]
梁CDのウェブの降伏せん断力Qyを求める
梁CDは曲げ降伏するかせん断降伏するかを判定する
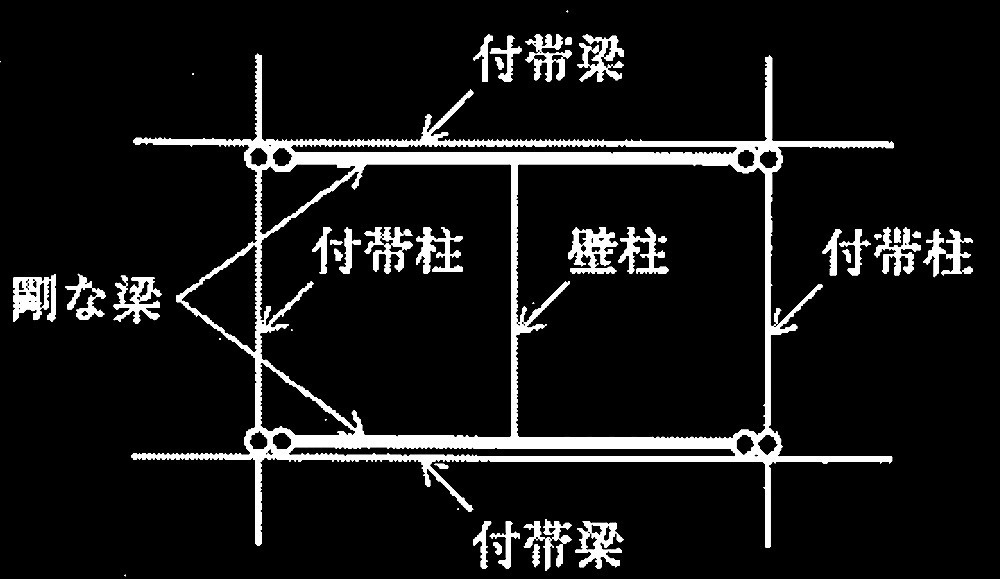
[ No.4 ]
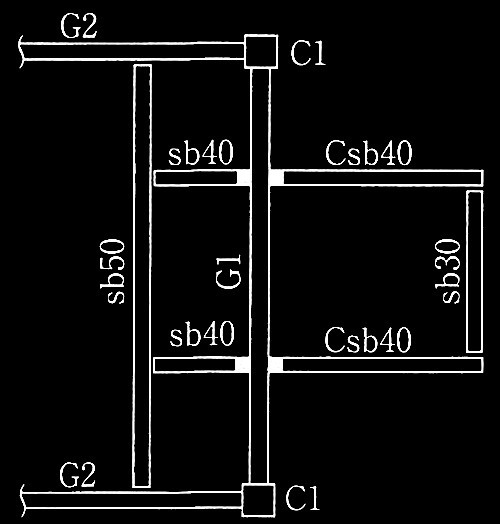
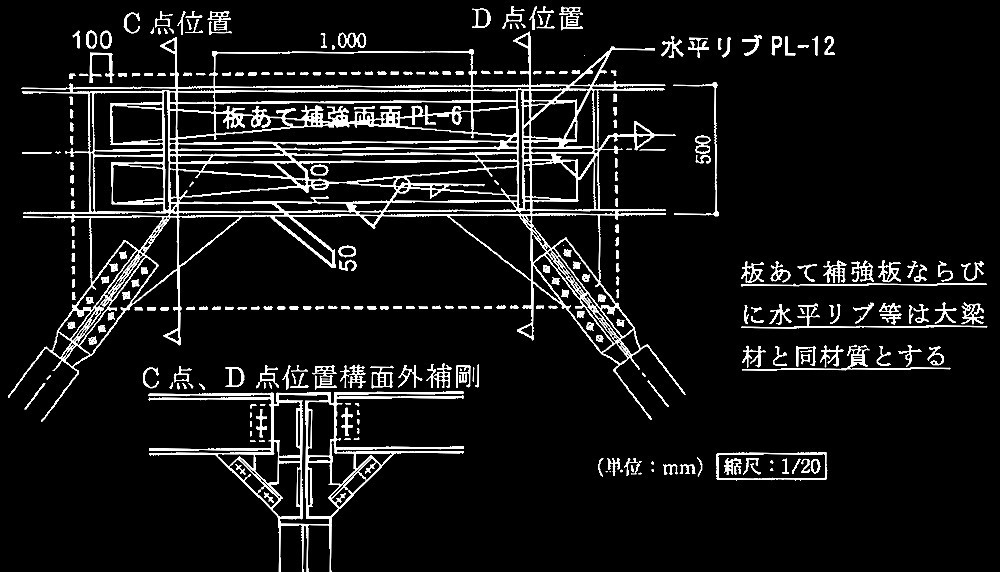
以上の解答を踏まえて、ブレースと梁の接合部が答案用紙の架構図のような場合、座屈拘束ブレースが安定してエネルギー吸収を行うために、構面外の安定性に対するv補剛とせん断耐力に対する補強を行った梁CDの接合部の納まりをスケッチせよ。ただし、補剛・補強範囲は破線枠内とする。
問題3
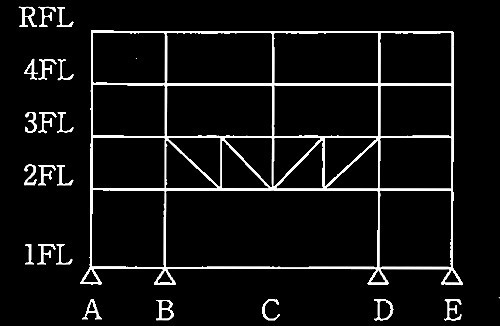
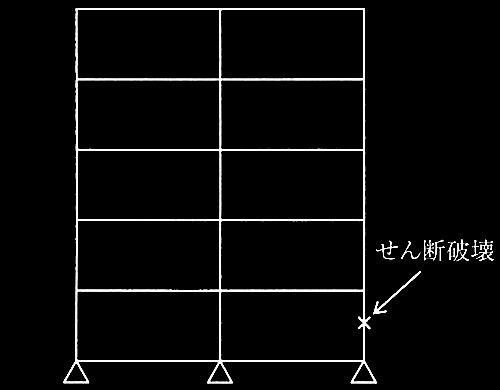
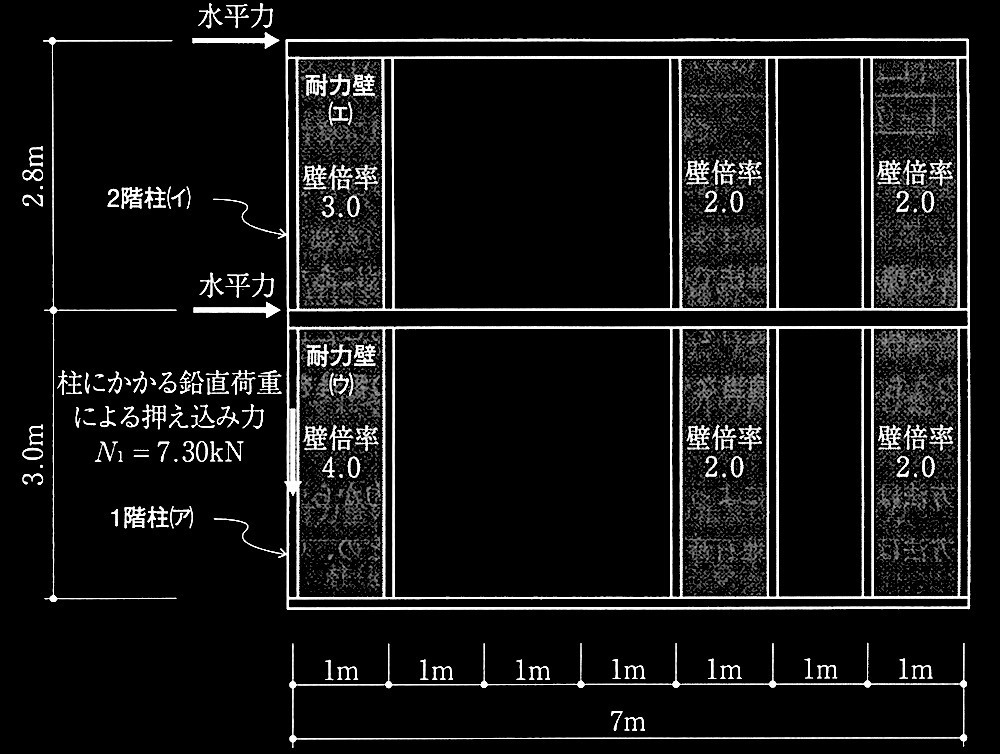
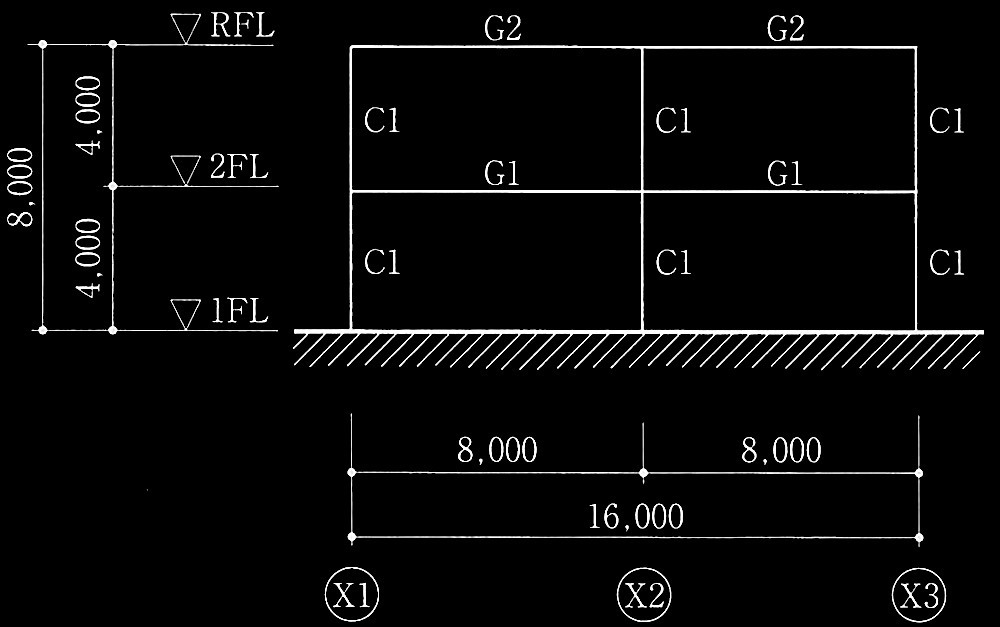
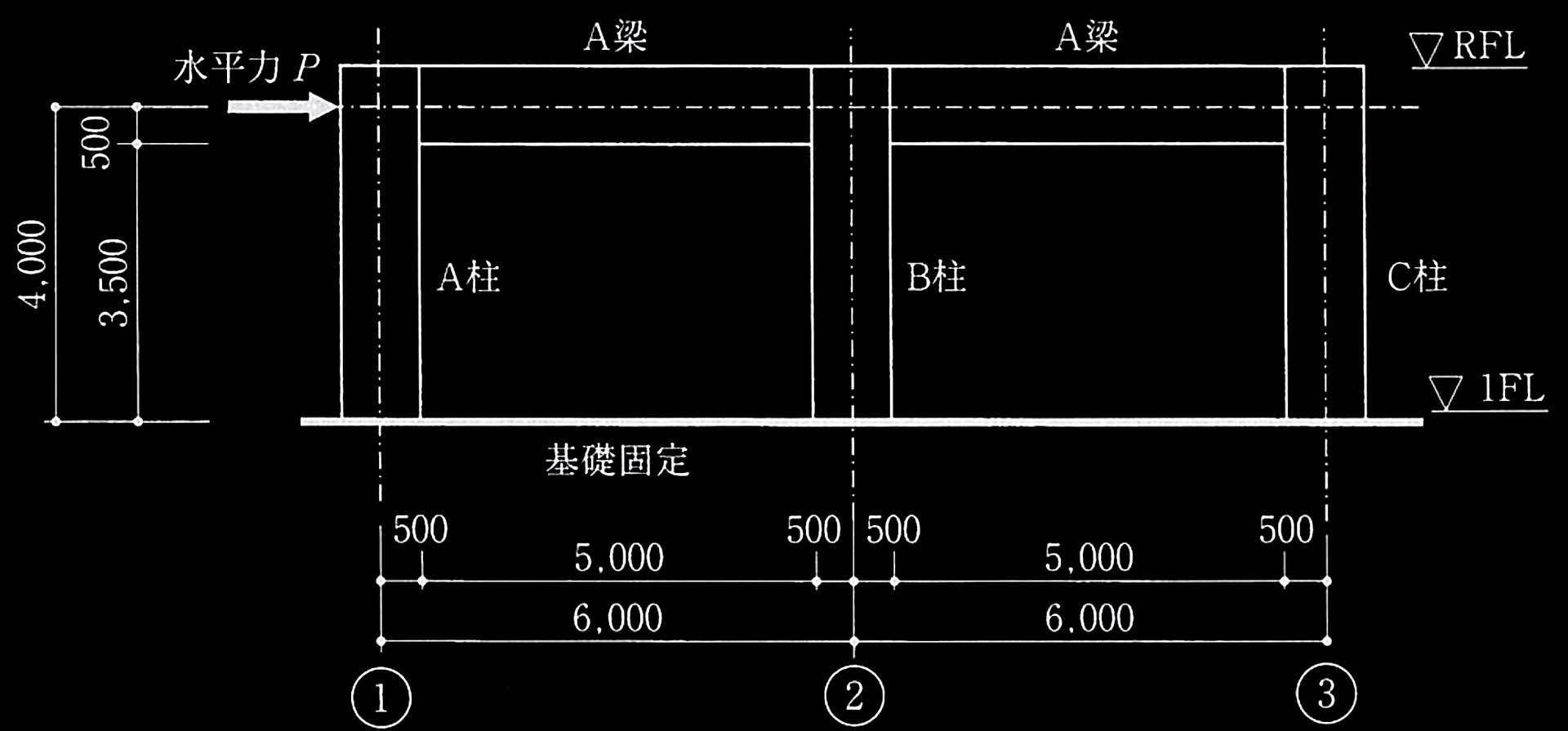
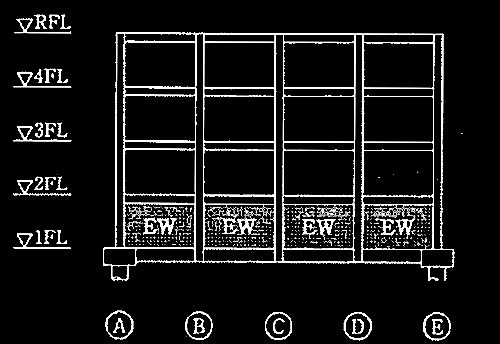
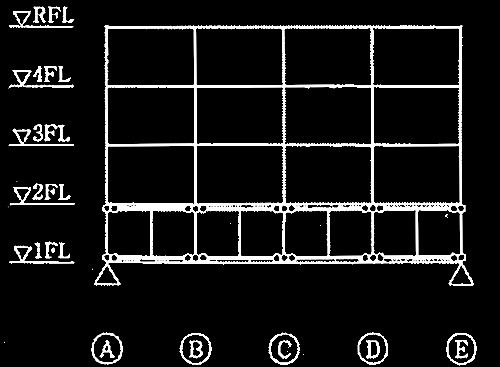
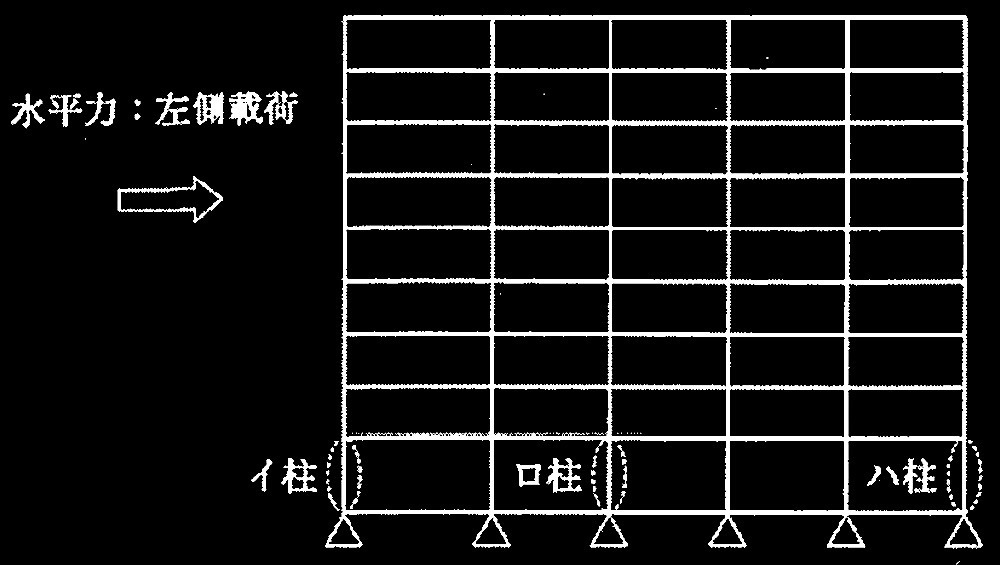
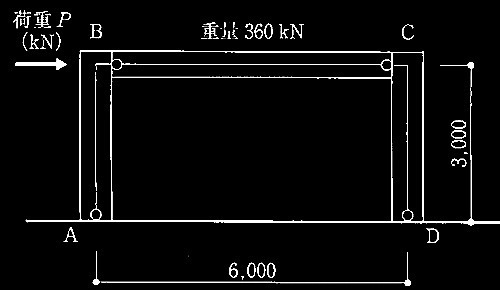
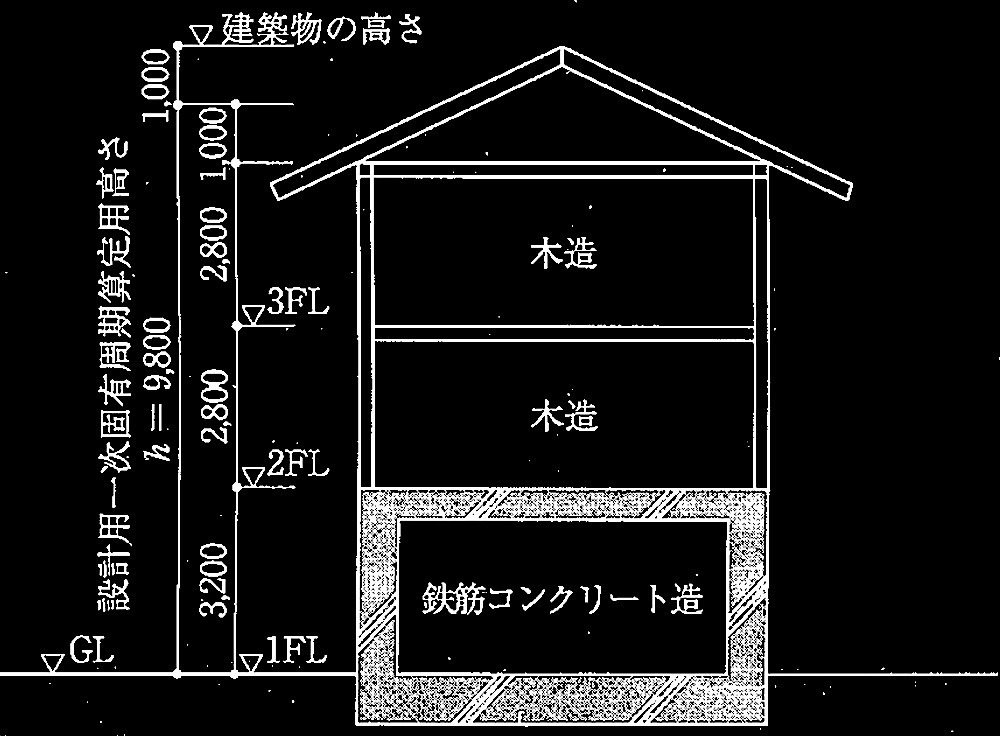
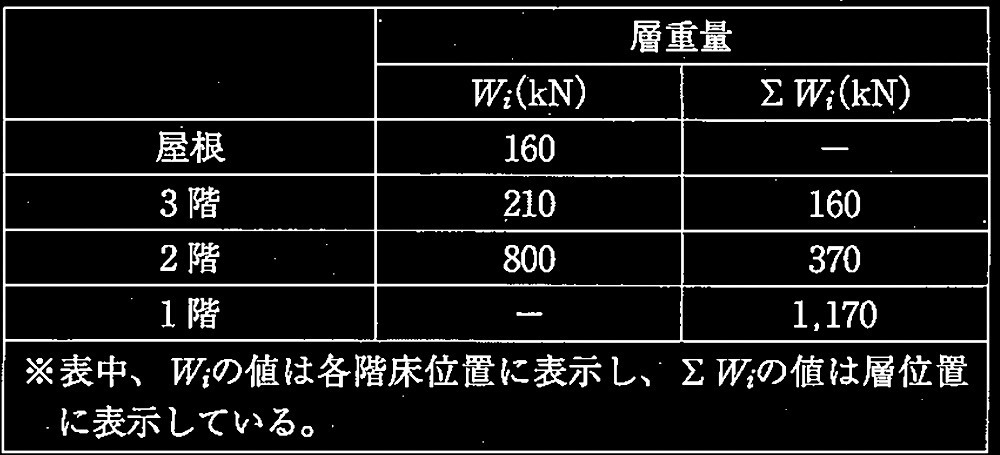
1層の鉄筋コンクリート造平面架構
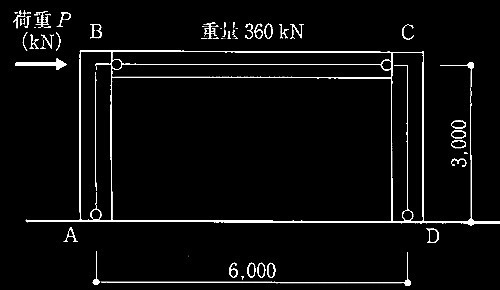
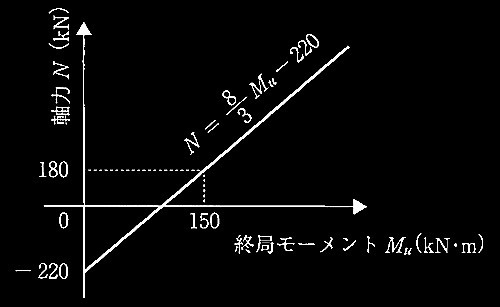
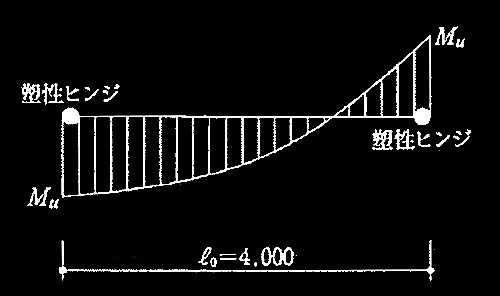
[ No.1 ]
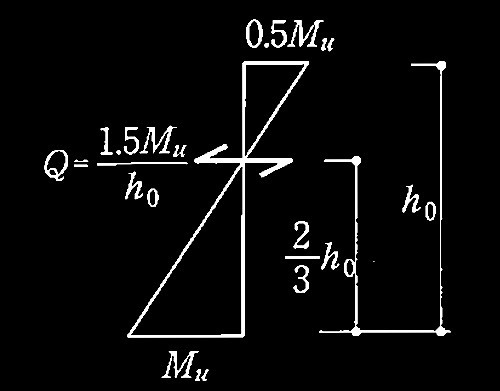
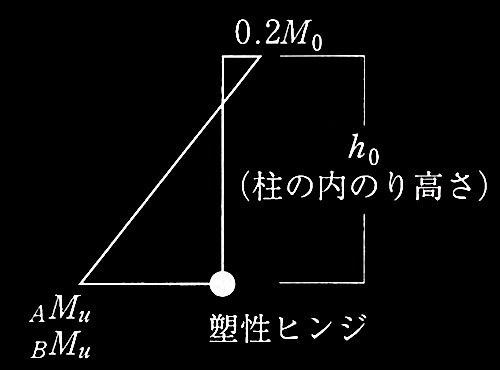
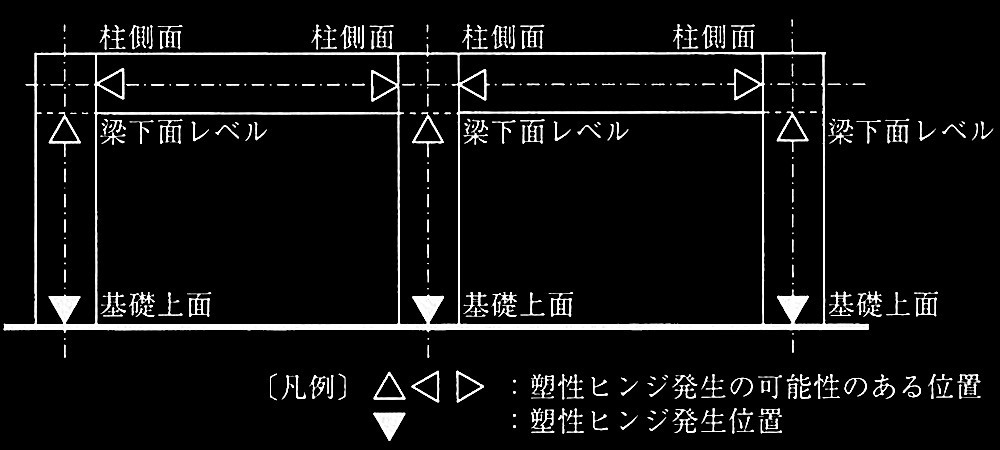
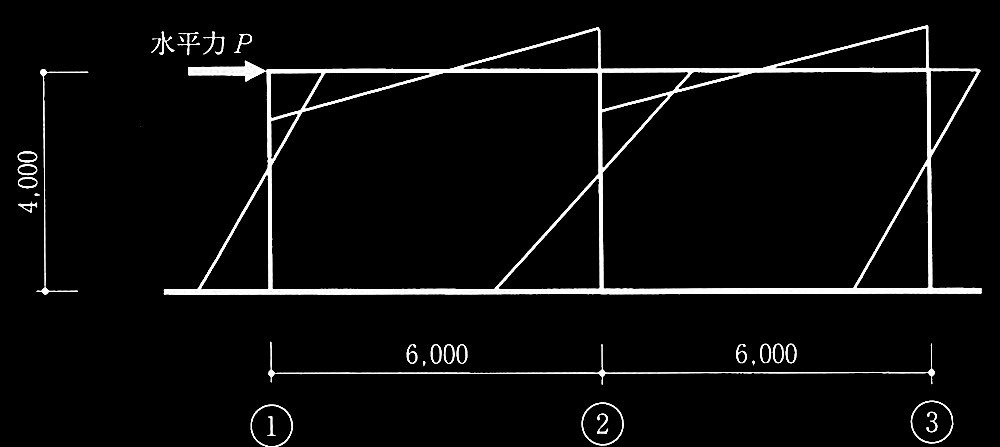
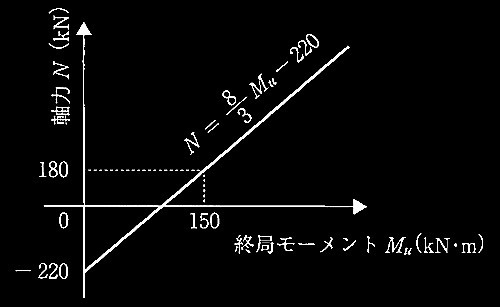
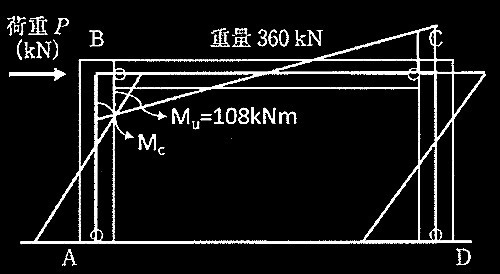
降伏ヒンジが形成されて崩壊メカニズムが形成されたときの
柱の軸力、終局モーメント、水平力、保有水平耐力
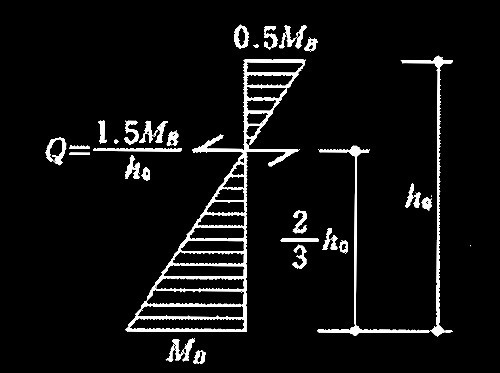
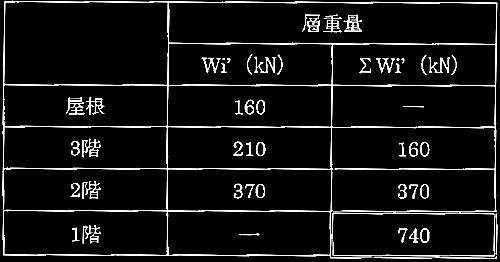
[ No.2 ]
必要保有水平耐力Qunを求める
[ No.3 ]
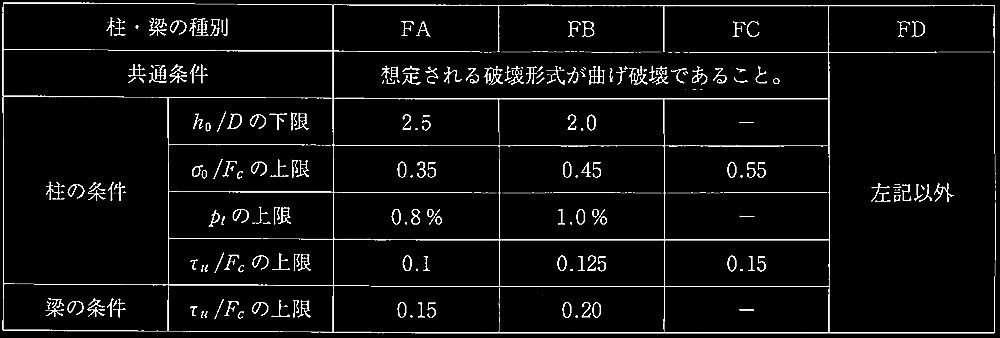
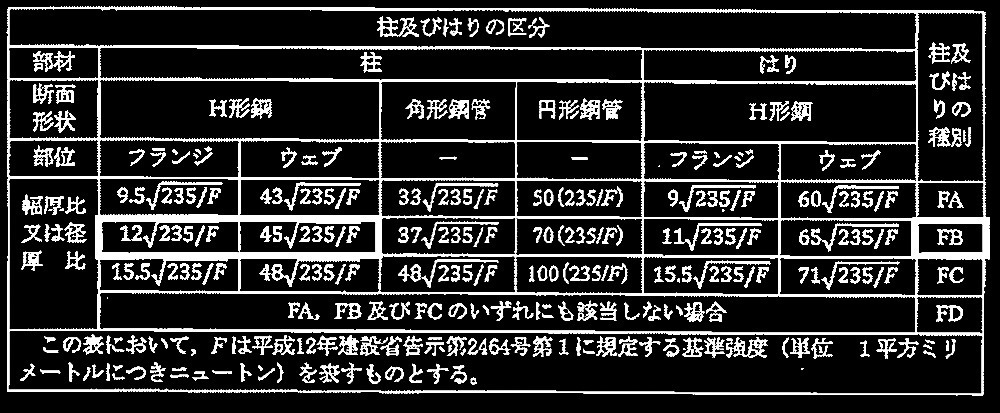
ptが小さい柱の場合、部材はFA又はFBに分類
ptが大きくなると部材はFDに分類されるような破壊形式になる。
ptの上限は この破壊形式の防止を目的として規定されている。
その破壊形式とその力学的特徴を簡潔に記述する。
(選択理由記述式4肢択ー問題)
No.1~No.10
No.1 一様断面の完全弾塑性体の連続梁
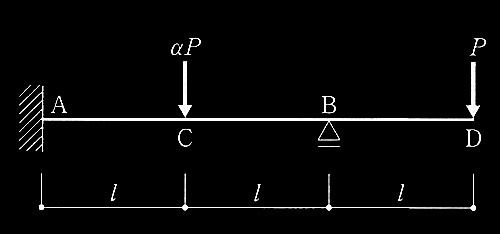
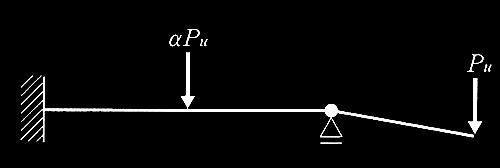
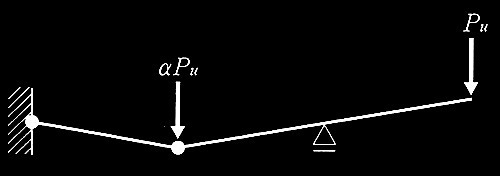
No.2 鉄筋コンクリート造
No.3 構造計画・構造解析
No.4 耐震設計
No.5 鉄骨構造
No.6 鉄筋コンクリート造の構造設計
No.7 木質構造の構造設計
No.8 免震構造•制振構造
No.9 地盤•基礎
No.10 耐霙診断・耐雛補強
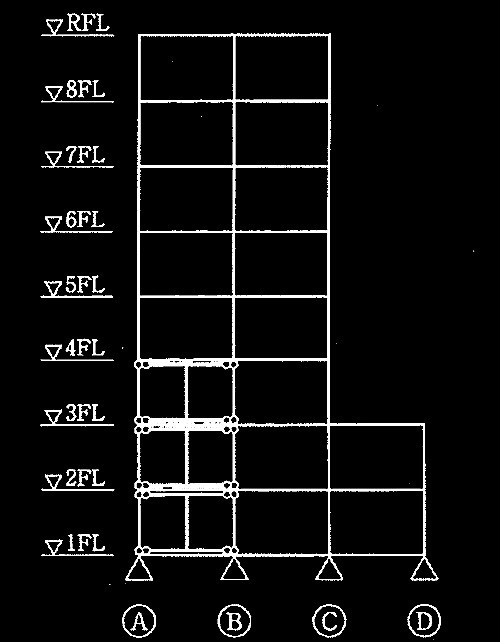
問題1
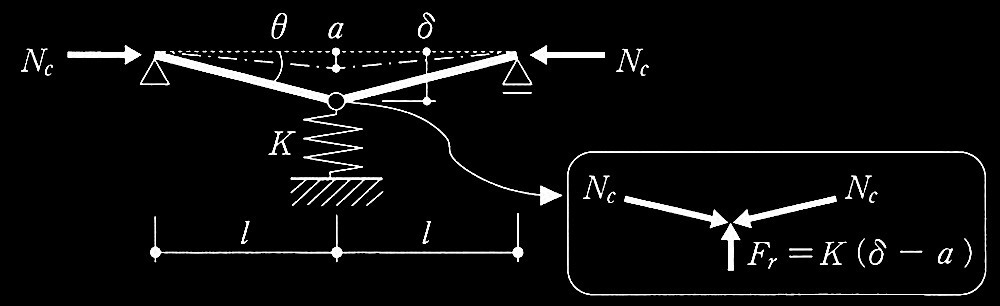
筋かい付き鉄骨架構及び座屈補剛モデル
本架構の接合部は保有耐力接合
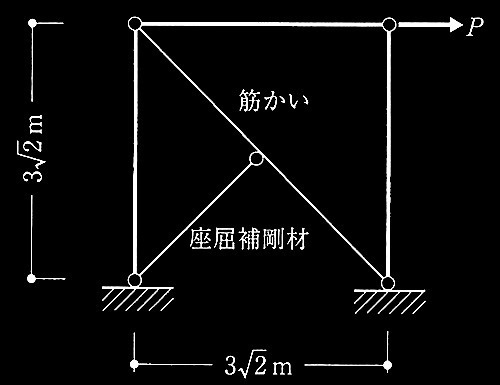
[ No.1 ] 筋かい材はH形鋼(SN400材:F値235 N/mm2)
筋かいの短期許容圧縮耐力見を求める。
[ No.2 ]
必要補剛力は圧縮力の2 %、
補剛材の剛性は実験と解析に基づき、4N/ℓk以上としている。
座屈補剛材に要求される必要補剛力Fr 及び必要補剛材剛性 K を求める。
[ No.3 ]
元たわみがある場合の座屈補剛材に要求される剛性と補剛力を求める。
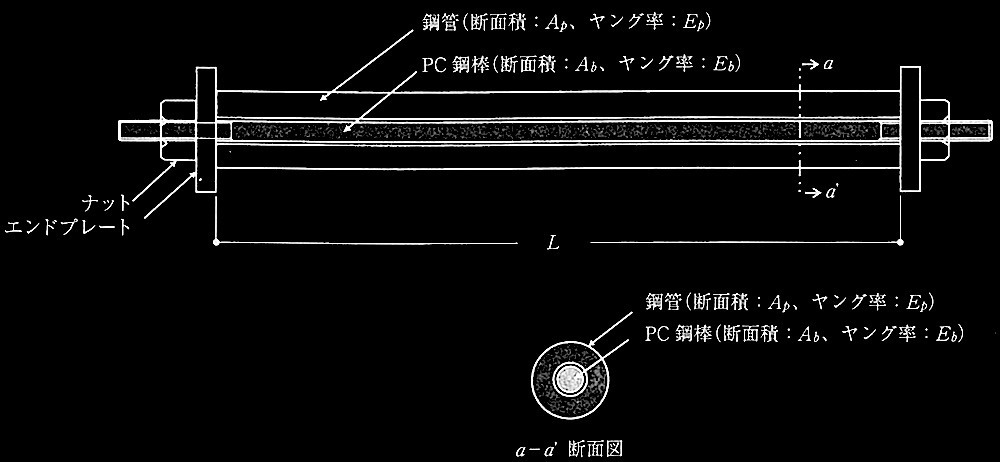
No.1 PC鋼棒が挿入された鋼管
No.2 コンクリートの特性及び鉄筋コンクリート造の構造設計
No.3 構造計画・構造解析
No.4 耐震設計
No.5 木質構造の構造設計
No.6 鉄骨構造
No.7 鉄筋コンクリート造部材の変形性能
No.8 免震構造・制振構造
No.9 地盤・基礎
No.10 建築物の耐震診断・耐震補強
構造設計(記述式)
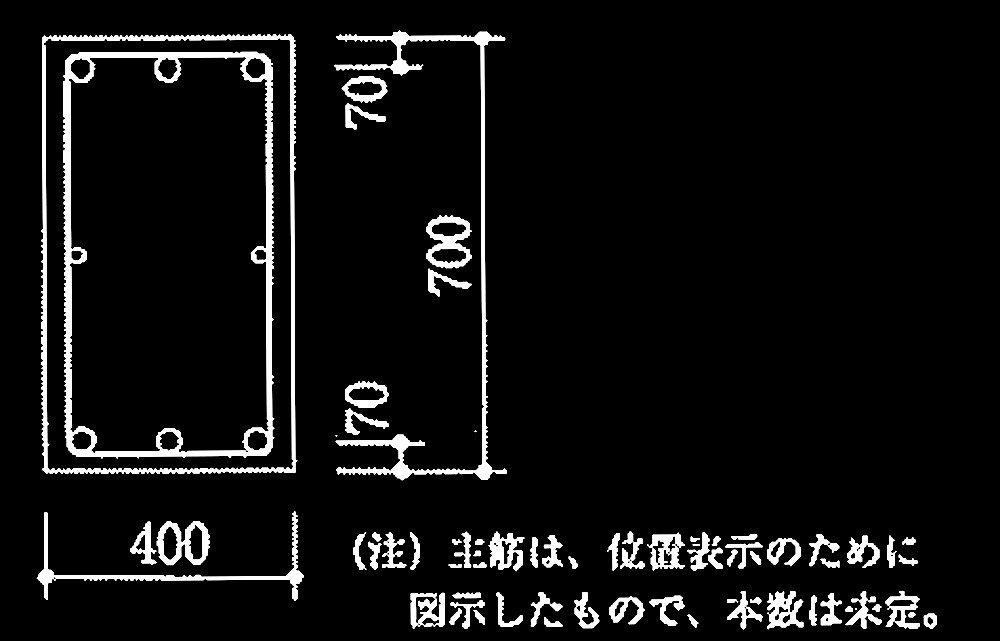
問題1鉄筋コンクリート造柱の断面性能
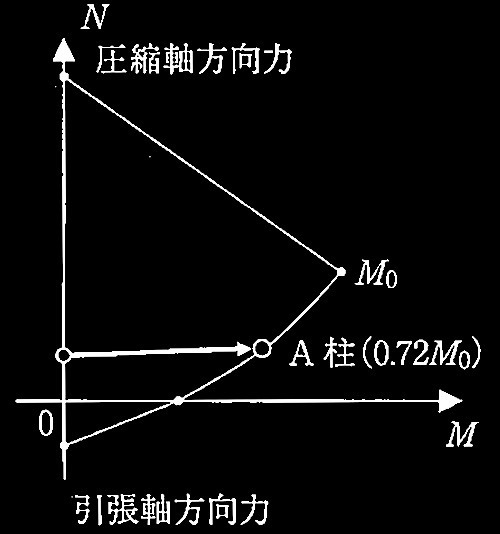
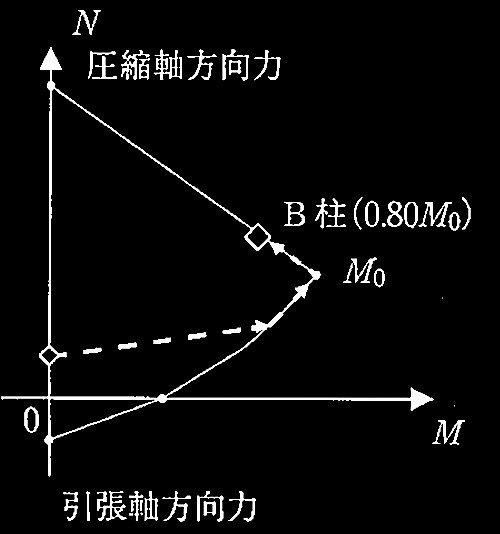
[ No.1 ]
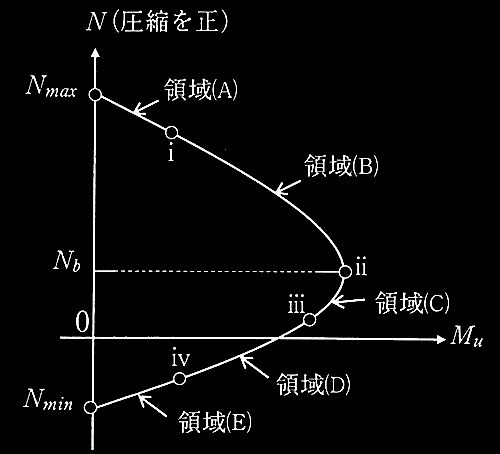
一定軸力の下で曲げ終局状態に達する柱
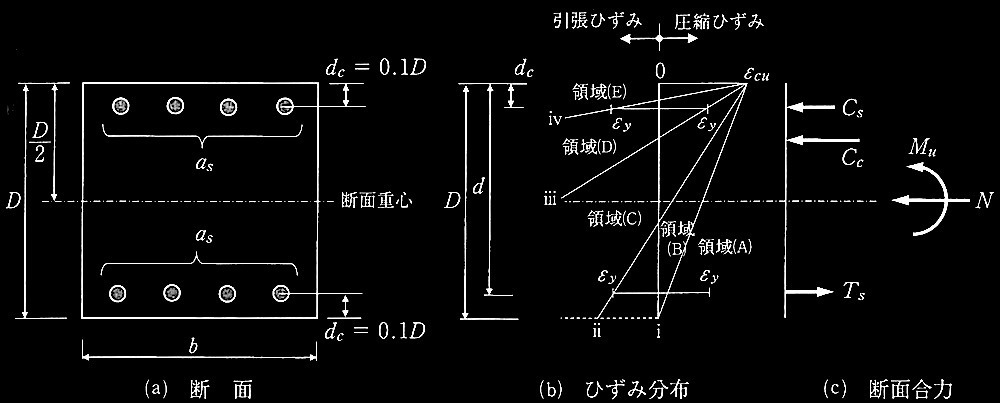
領域(A)~領域(E)のどの領域に相当するかを選ぶ
① 引張鉄筋も圧縮鉄筋も引張降伏している状態。
② 引張鉄筋は引張降伏していて、圧縮鉄筋は圧縮降伏している状態。
③ 引張鉄筋は引張降伏していて、圧縮鉄筋は弾性範囲の状態。
④ 全断面が圧縮の状態。中立軸は断面外にあり圧縮応カブロックは適用できない。
⑤ 引張鉄筋は弾性範囲で、圧縮鉄筋は圧縮降伏している状態。
[ No.2 ]
軸力が軸力Nb(圧縮を正)のとき、終局曲げモーメントMuを求める
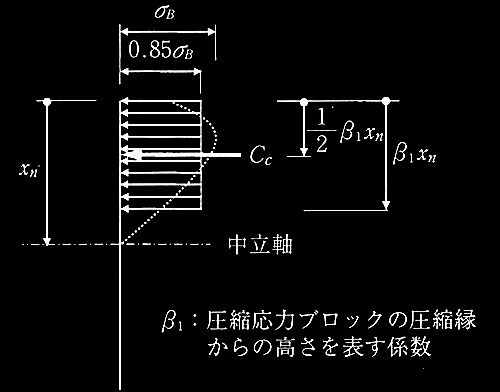
[ No.3 ]
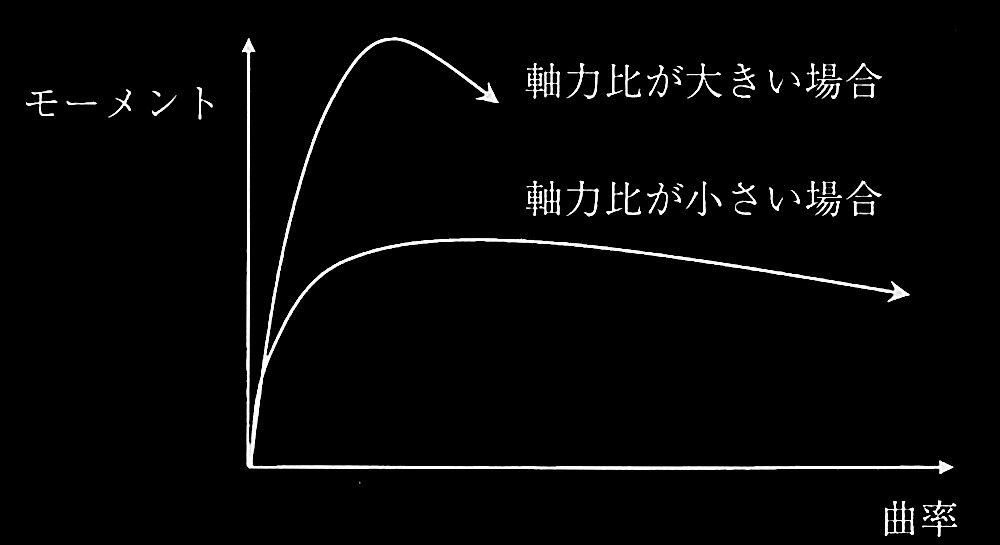
図4は同断面で、軸力比(作用軸力の断面圧縮耐力に対する比)のみが異なる鉄筋コンクリート造柱の断面のモーメントと曲率の関係を表している。通常の軸力の範囲であれば、軸力比が大きい場合は、最大モーメントは大きくなり、限界変形(抵抗モーメントが最大モーメントから95%に低下したときの変形)は小さくなる。その理由をそれぞれ記述せよ。
問題2
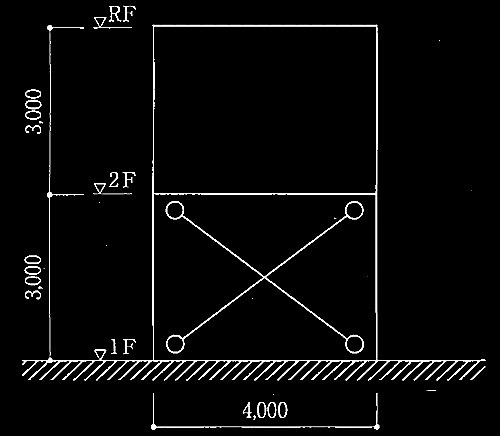
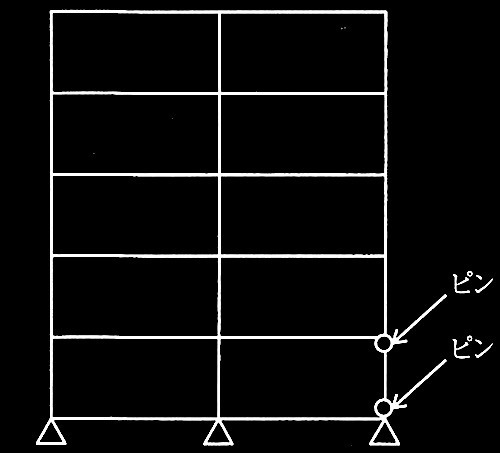
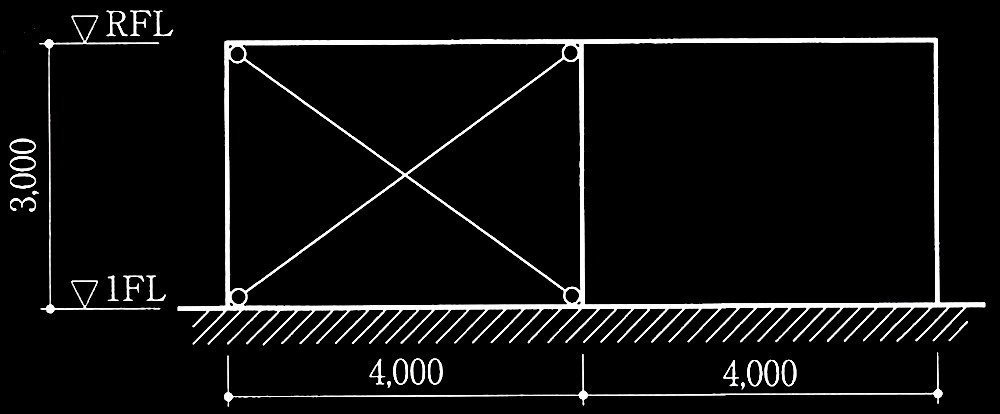
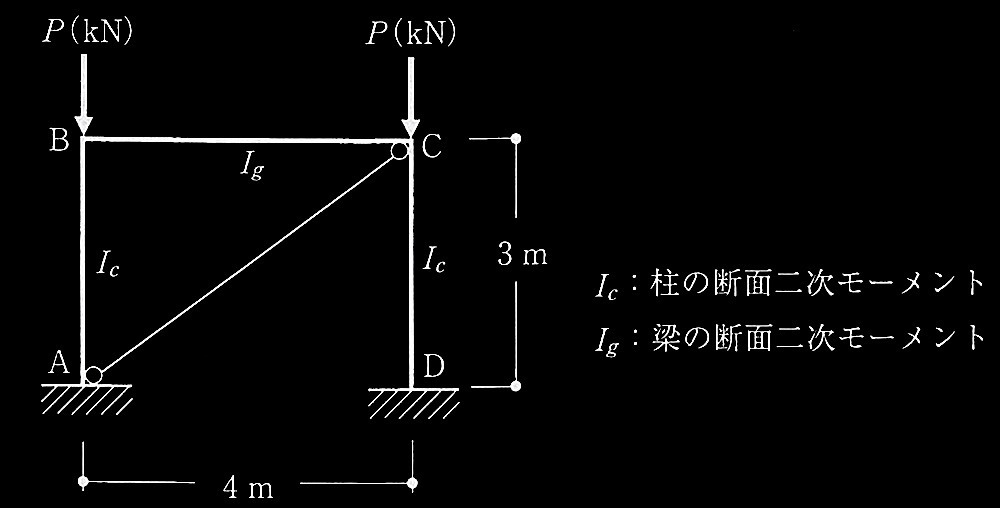
長期鉛直荷重を受けるブレース付き鉄骨造門型骨組の柱の座屈
[ No.1 ]
柱が表1に示す角形鋼管、梁が剛体とみなせる場合
① 両端固定で節点の水平移動がないものとして、柱の座屈長さを求めよ。
② 柱の長期許容圧縮応力度を求めよ。
③ 柱1本の長期許容圧縮力を求めよ。
[ No.2 ]
柱が表1に示す角形鋼管、梁が表1に示すH形鋼の場合
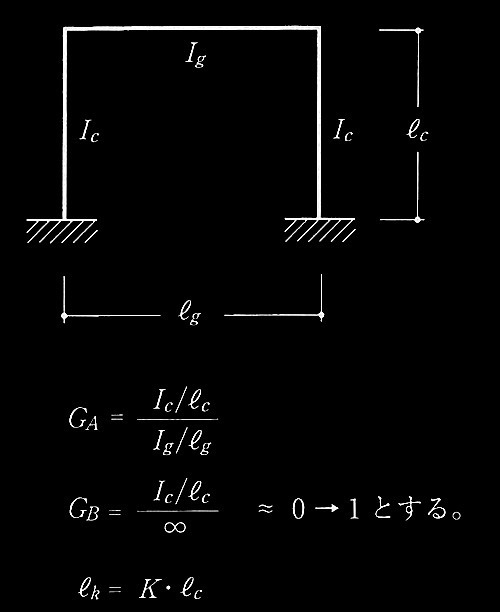
① 図2を用いて座屈長さ係数 Kを求める場合のGA値を求めよ。
② 図2を用いて座屈長さ係数 Kの値を求めよ。なお、GB= 1とする。
③ 座屈長さ係数Kを用いた柱の座屈長さを求めよ。
④ 柱の長期許容圧縮応力度を求めよ。
⑤ 柱1本の長期許容圧縮力を求めよ。
[ No.3 ]
ブレースが表1に示す等辺山形鋼の場合
① ブレースの長期許容圧縮力を求める。
② [ No.2 ]の場合について、ブレースが柱頭の水平移動を拘束できるか否かを検討する。
なお、ブレースが負担する水平力は、柱2本の長期許容圧縮力の2%とする。
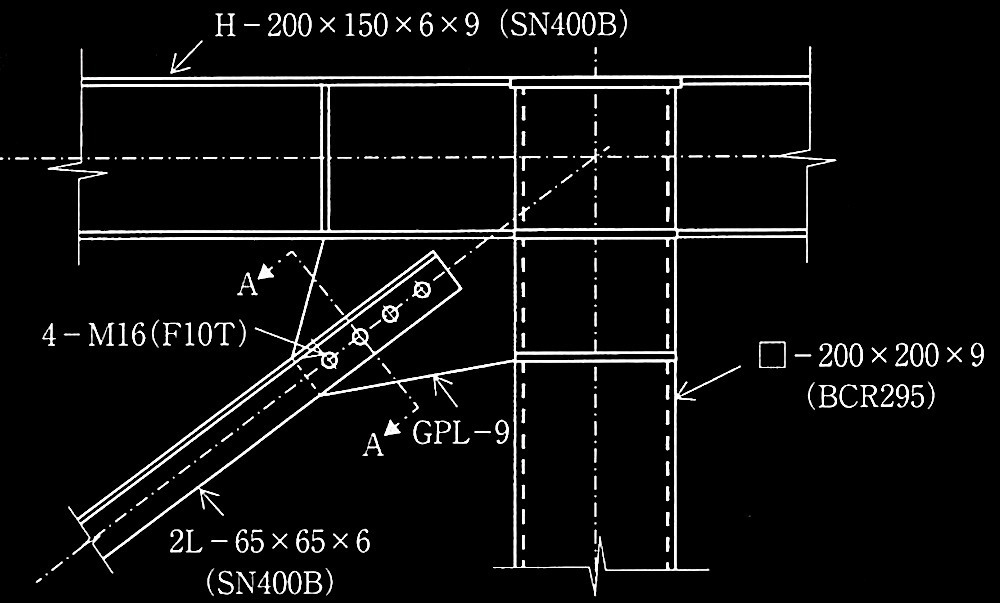
③ [ No.2 ]の場合について、節点Cにおけるブレースと柱梁接合部の納まりをスケッチする。
使用するボルトは、m20(F10T)とし、1本当たりの1面摩擦に対する長期許容せん断力は、46.2 kNとする。
問題3
[ No.1 ] 免震ピットの立上り壁に作用する偏土圧
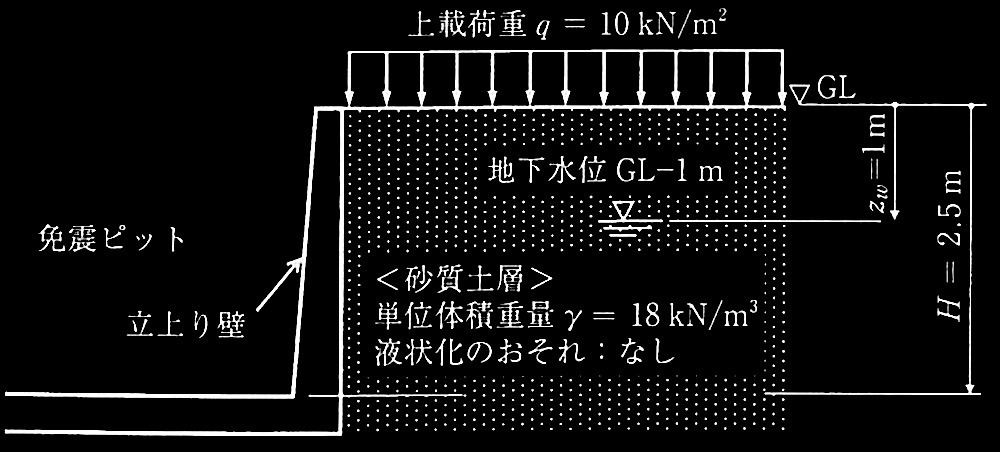
① 常時作用する土圧、水圧、及び「土圧と水圧の合計」を算定して、答案用紙のグラフ①にそれぞれの深さ方向の分布を記入する。
立上り壁脚部の幅1mあたりに常時作用するせん断力QL(kN/m)を求める。
② 地震時に作用する土圧、水圧、及び「土圧と水圧の合計」を算定して、答案用紙のグラフ②にそれぞれの深さ方向の分布を記入する。
ただし、土圧は破線、水圧は一点鎖線、「土圧と水圧の合計」は実線で示すこと。それぞれの線には、深さ0m(地表面)、1.0 m(地下水位点)及び2.5m(壁脚部)での土圧•水圧の値を記入すること。なお、地盤は液状化しないものとし、極めて稀に発生する地震動を想定して、地震時土圧係数 KEAは1.0とし、水圧は静水圧とする。
[ No.2 ] 建築物の直接基礎(べた基礎)の設計
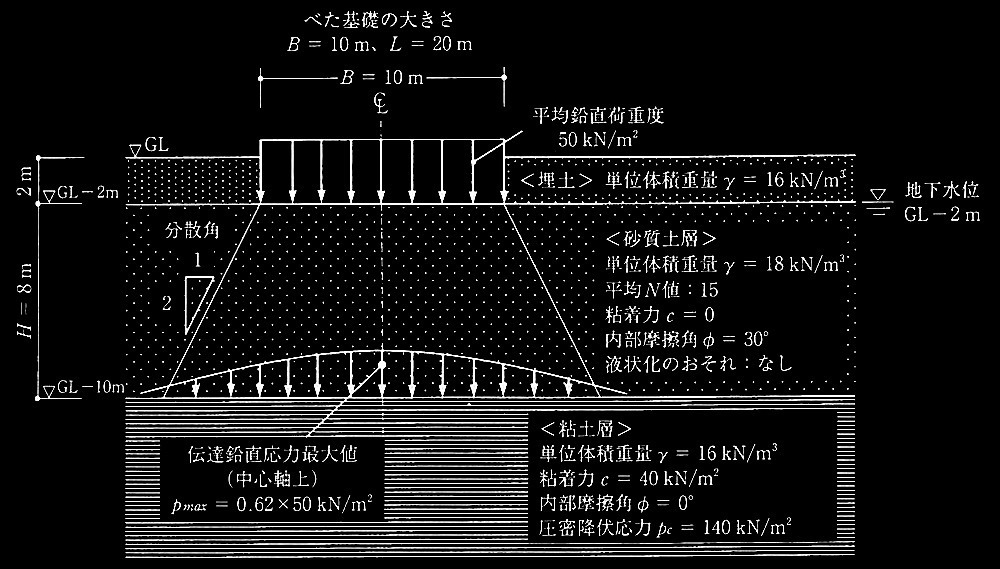
① 基礎直下の砂質土層の長期許容鉛直支持力度qa1を、式(2)を用いて求める。
ただし、根入れ深さDf には埋土部分は含まれないものとする。
② 直接基礎底面(GL -2m) に作用する鉛直荷重が、分散角1/2で粘土層表面(GL-10m)に ( B + H )•( L + H )の大きさに均等に載荷されるものとして、直接基礎底面 ( GL–2 m )に換算した粘土層の長期許容鉛直支持力度qa2を、式(3)を用いて求める。
ただし、根入れ深さDfは砂質土層厚Hとし、埋土部分は根入れ深さに含まれないものとする。
③ 圧密沈下が発生するか否かを計算で求める。
ただし、基礎の鉛直荷重度による粘土層の上面 ( GL-10m ) の中心軸上の伝達鉛直応力の最大値Pmaxは、図2に示すように 0.62 × 50 kN/m2とする。圧密沈下の検討では埋土の重量も考慮するものとする。
No.1 建築物の耐震設計
No.2 図A~Dに示す鉄骨柱の座屈耐力Pの大小関係
No.3 静定平面トラスがあり、トラス I はA点に、トラス Ⅱ はB点に、それぞれ2Pの鉛直荷重を受けている。それぞれの載荷点の鉛直変位δAとδBの組合せをもちめる。、次のうちどれか。なお、全ての部材について断面積をA、ヤング係数をEとする。
No.4 構造材料
No.5 建築物の構造計画
No.6 建築物の構造解析
No.7 荷重・外力に関する
No.8 耐震設計
No.9 耐風設計
No.10 木質材料及び木質構造
No.11 木質構造
No.12 鉄骨構造
No.13 鉄骨構造
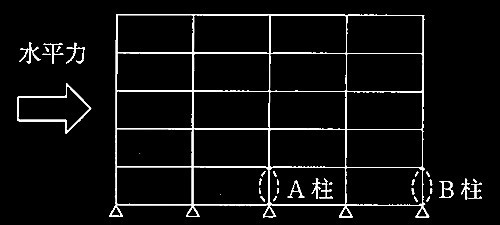
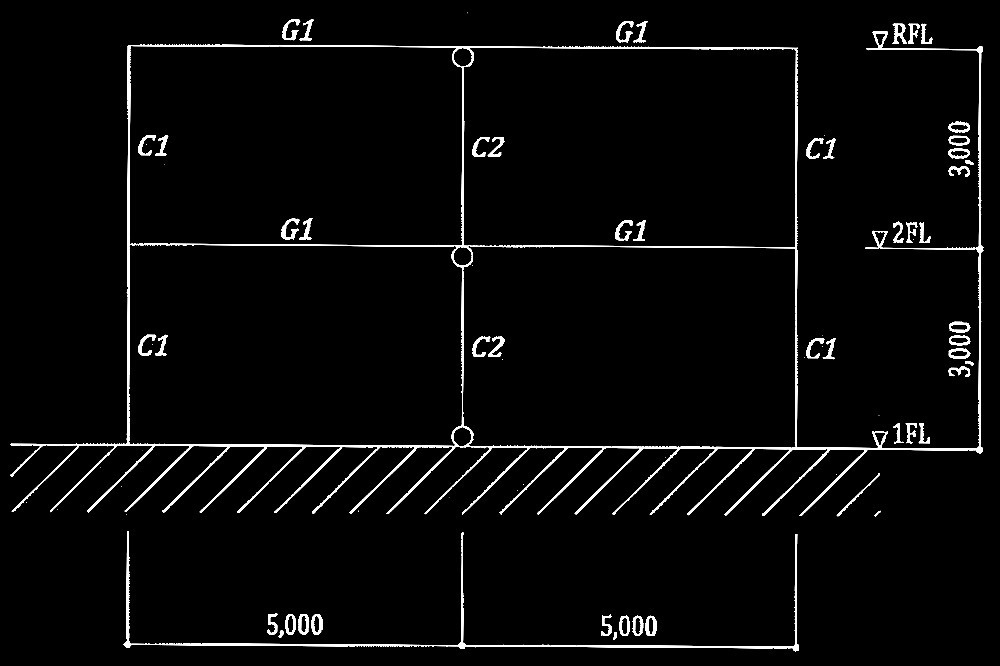
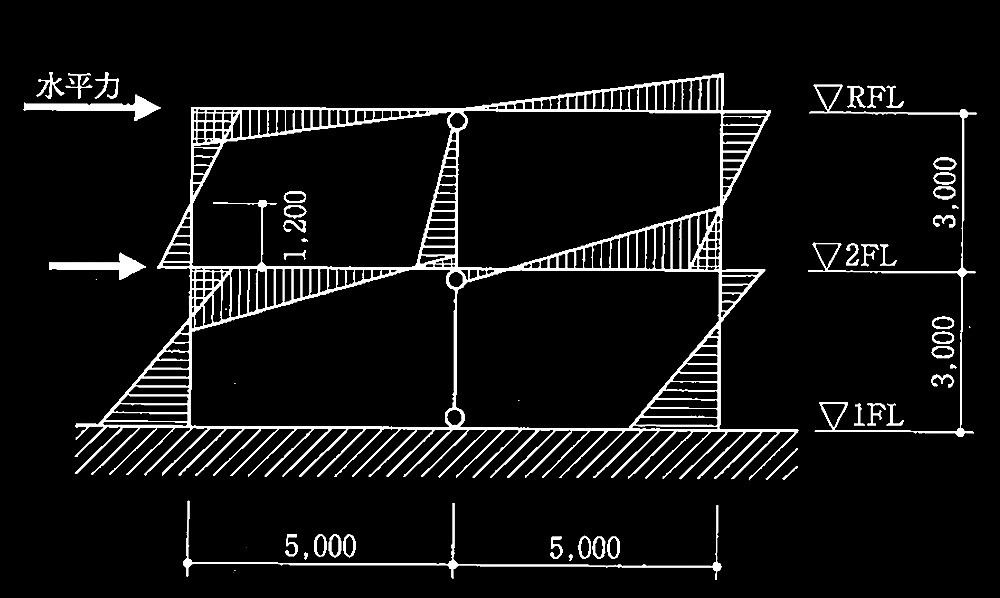
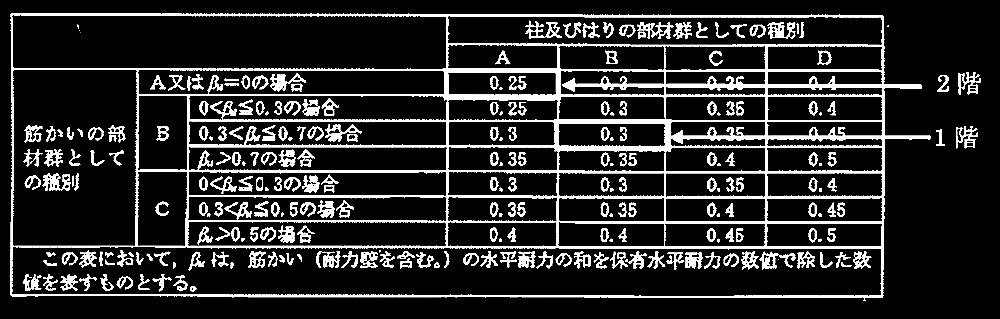
No.14 鉄筋コンクリート造2層多スパン均等平面骨組に水平力が作用
1階柱、2階柱梁接合部、及び2階柱にひび割れの方向
No.15 鉄筋コンクリート構造
No.16 免震構造・制振構造
No.17 地盤・基礎
No.18 地盤・基礎
No.19 建築物の非構造部材
No.20 既存建築物の耐霙診断・耐霙補強
(記 述 式)
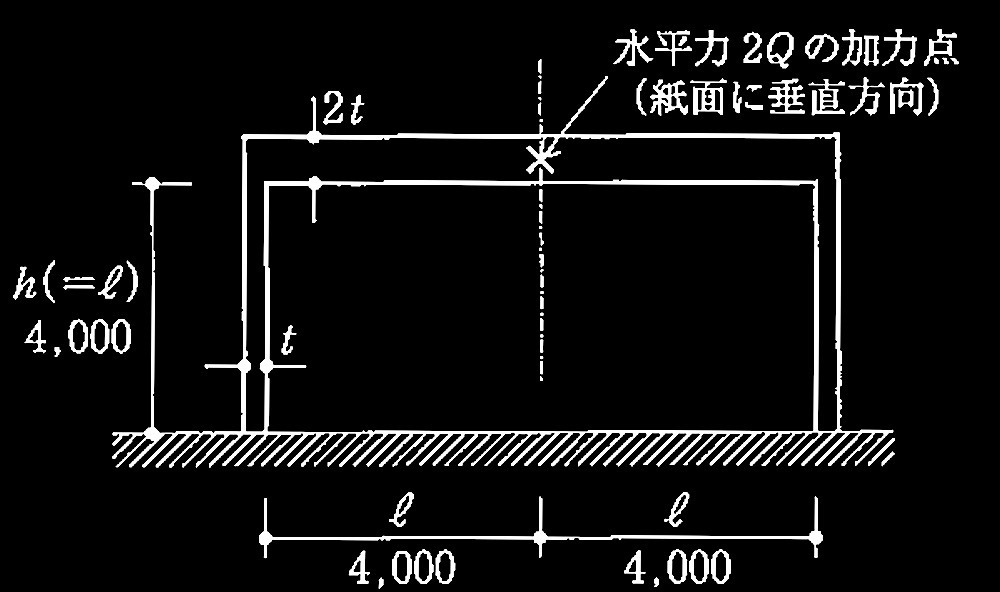
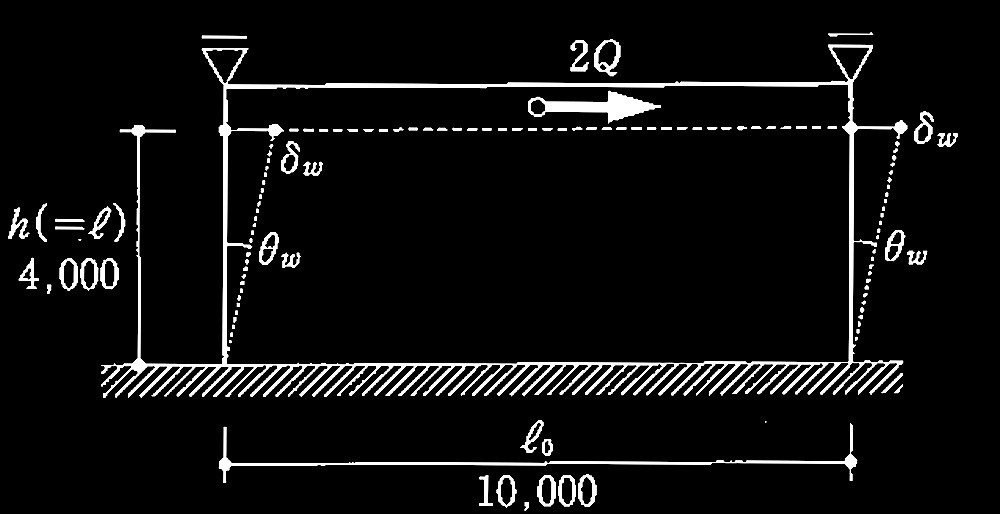
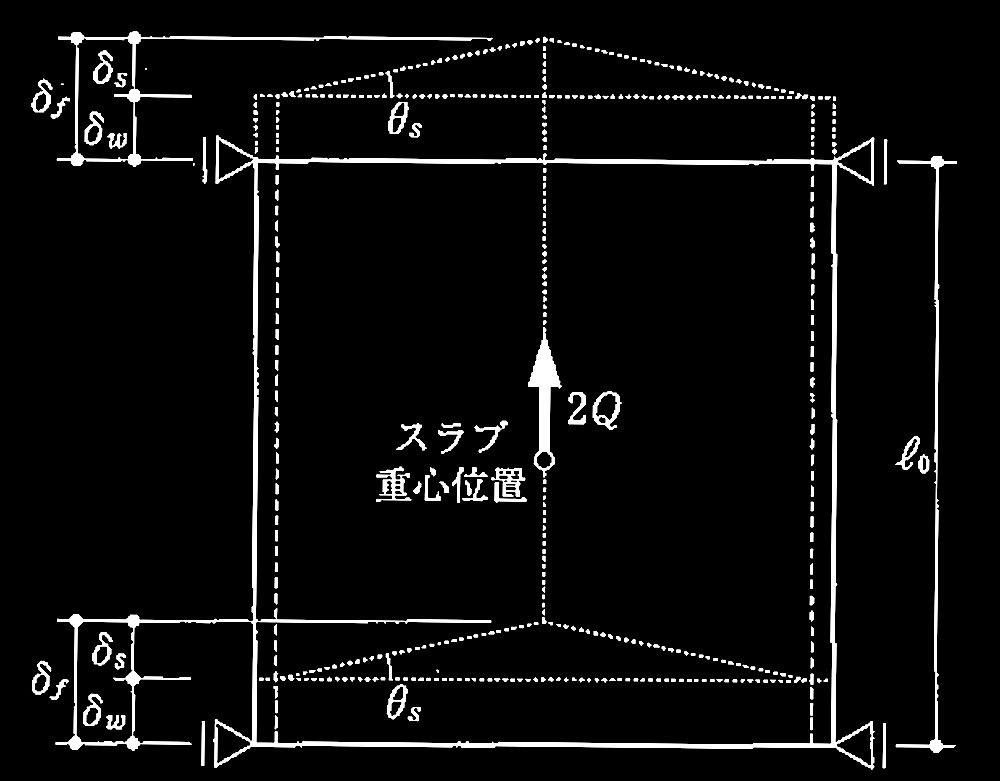
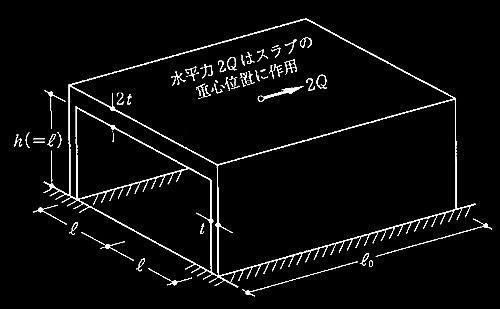
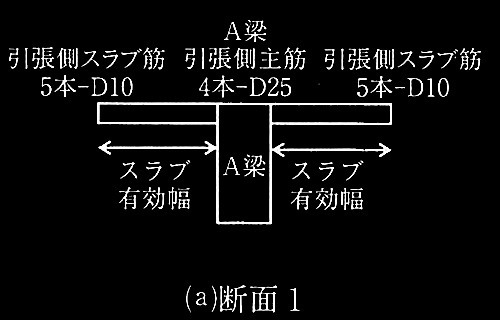
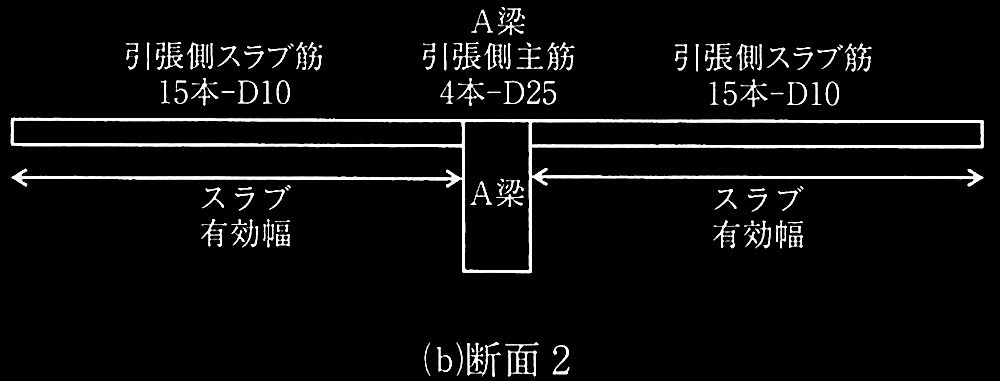
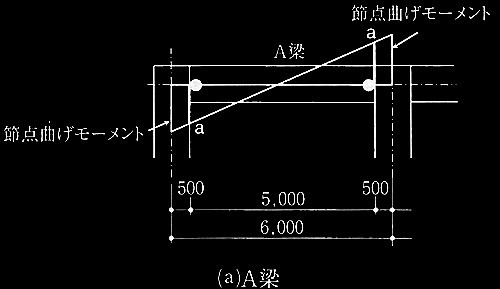
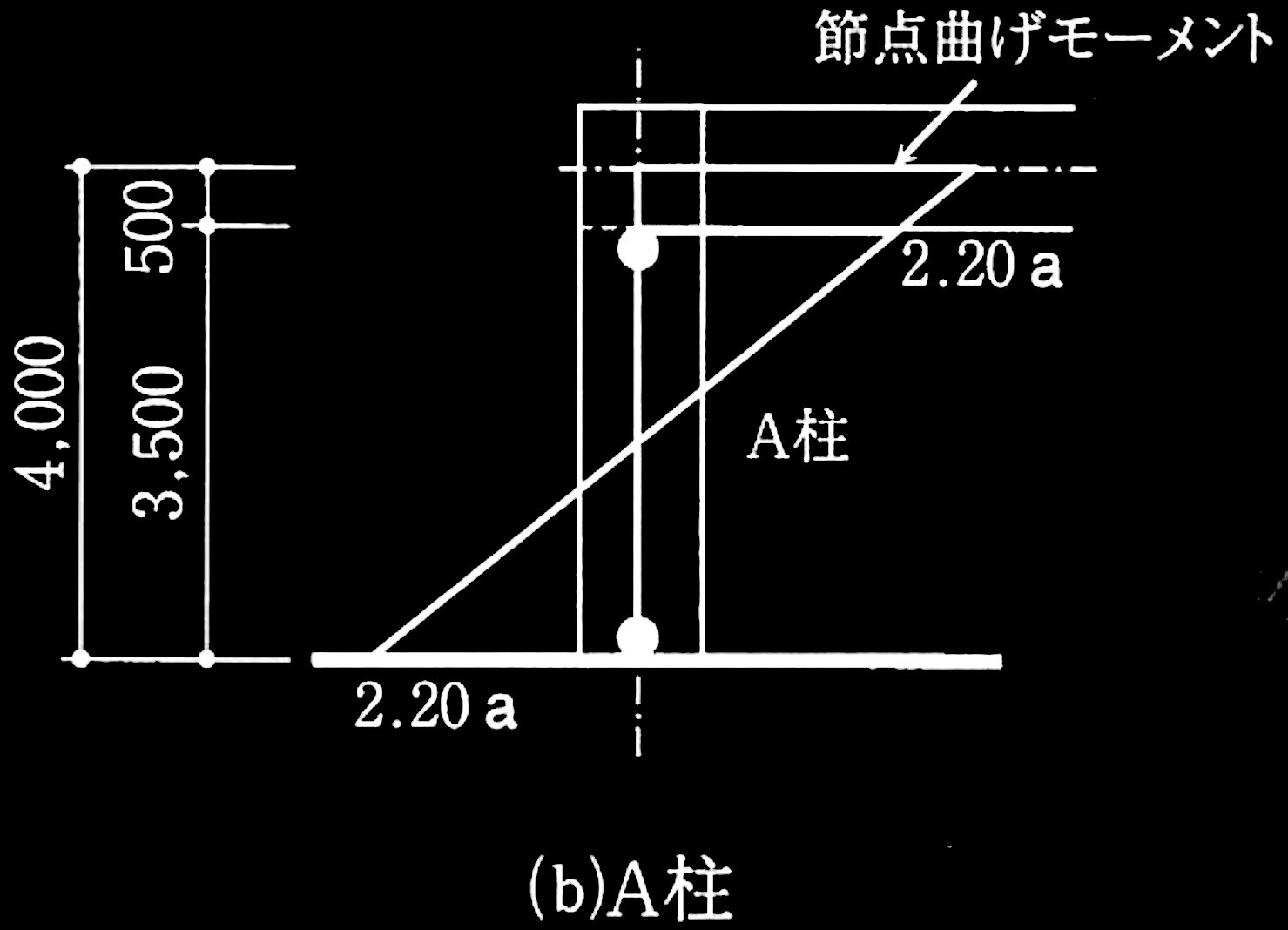
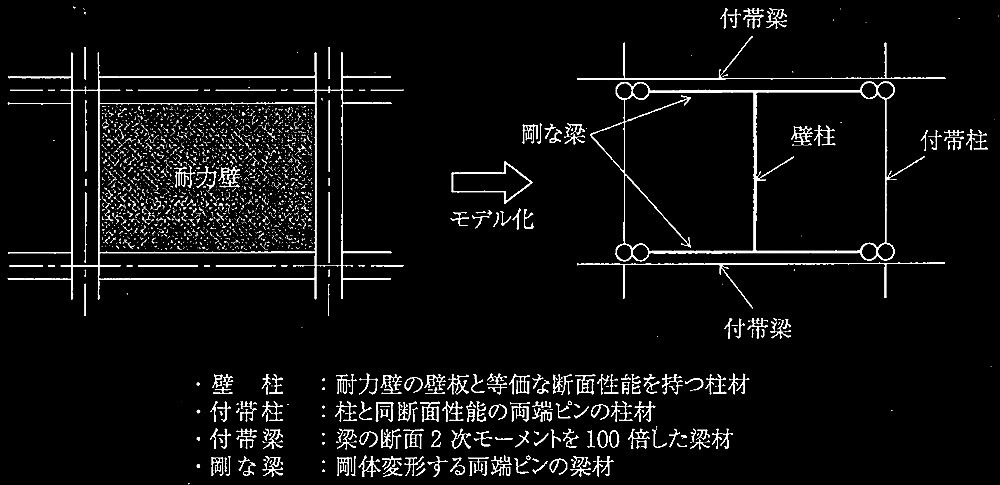
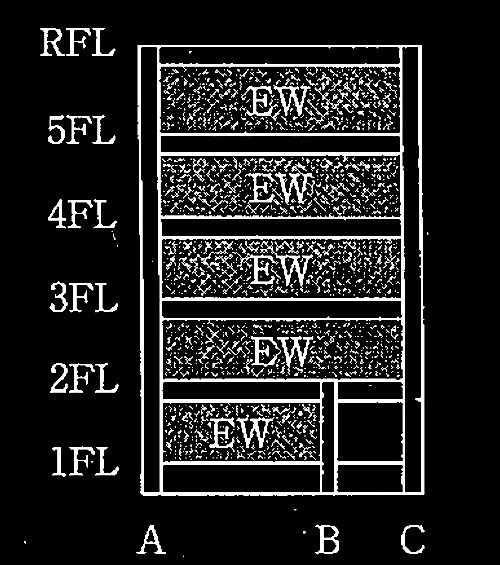
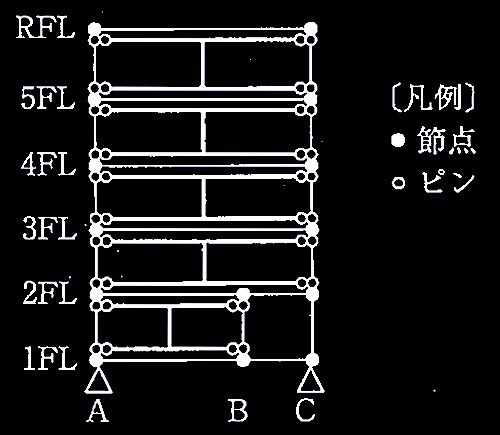
問題1鉄筋コンクリート造の耐力壁とスラブ