2024年07月10日
令和元年度修了考査 法適合確認 問題3
鉄筋コンクリート造建築物の耐震計算ルート3による設計に関する次の設問について解答せよ。
[ No.1 ]
鉄筋コンクリート柱の種別の判定に関する次の①~④の設問に解答せよ。対象とする柱(以下、「当該柱」という。)の諸元は図1、図2及び表1による。なお、当該柱の種別判定はX方向を対象とし、当該柱に取り付く梁の種別は考慮しないものとする。
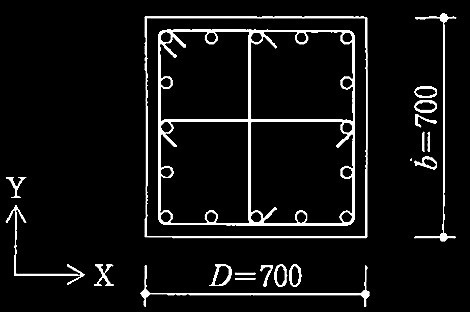
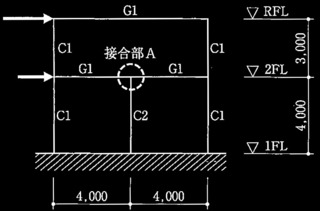
図1 柱断面 (単位:mm)
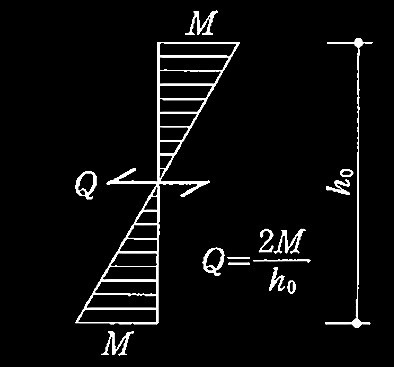
図2 柱の曲げモーメント分布
表1 当該柱の柱頭及び柱脚の諸元(計算に用いる値)
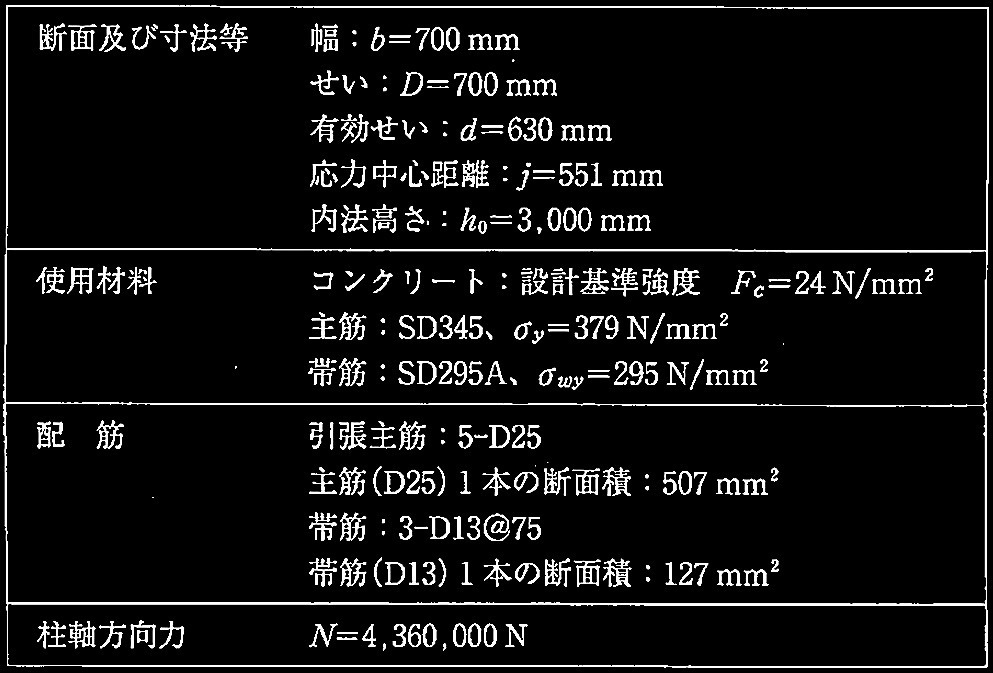
くその他の諸条件>
(a) 柱の種別判定に用いる破壊モードとしては、柱頭・柱脚に塑性ヒンジが生じるモード(曲げ破壊)及び柱がせん断破壊するモード(せん断破壊)を考慮する。
(b) 柱のせん断余裕度(αs)は、柱の曲げ破壊時せん断力(Qmu)に対する柱のせん断終局耐力(Qsu)の比率とする。なお、Qmuの算定には長期せん断力は考慮しなくてよい。
(c) 柱のせん断余裕度(αs)が要求値(αsn)以上である場合には、柱の破壊モードは曲げ破壊とし、構造耐力上支障のある急激な耐力の低下のおそれがない破壊モードとしてよい。
① 当該柱の曲げ破壊時せん断カ(Qmu)を求めよ。なお、柱の曲げ終局モーメント(Mu)は式 (1) により求めるものとする。Qmuの単位はkNとし、小数第1位を四捨五入して表記せよ。
式(1)


答え
[ 解答解説 ]
at=507mm2 × 5本 = 2535 mm2
σy = 379 N/mm2
Fc = 24 N/mm2
D = 700 mm、b = 700 mm、N=4,360,000 N
より
Mu = 0.8 αtσyD + 0.5ND( 1 – N/ FcbD)
= 0.8 × 2535 × 379 × 700 + 0.5 × 4360000 × 700 × (1– 4360000 / 24 / 700 / 700)
Mu= 1498000000 Nmm
内法高さ:ho = 3,000mmより
Qmu = 2 × 1498000000 Nmm / 1000 / 3000mm=999 kN
② 当該柱のせん断余裕度(αs)を求めよ。なお、柱のせん断終局耐力(Qsu)は式(2)により求めるものとする。また、αsは小数第3位を四捨五入して表記せよ。
答え
[ 解答解説 ]
Pt= 2535 mm2 /(700mm × 700mm) × 100 = 0.517%
Q=2M/hoより
M/(Q・d) = M/ (2M/ho・d) = ho/2d = 3000mm / (2 × 630mm) =2. 381
aw= 127mm2 × 3本=381 mm2
s=75mm、pw=381mn2/(700mm × 75mm) = 0.007
σwy=295 N/mm2
σo=4, 360,000N/ (700mm × 700mm)
= 8.90 N/mm2く0. 4Fc=0.4 × 24N/mm2
= 9.60 N/mm2
j = 551mm
ただし、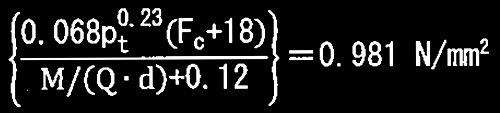
にて計算する
よって、
αs = Qsu/Qmu=1190kN/999kN=1.19
③ 当該柱の破壊モードを、上記①及び②の結果から推定せよ。なお、当該柱のせん断余裕度の要求値(αsn)は、1.1としてよい。
答え
[ 解答解説 ]
αs = 1.19 ≧ αsn = 1.1のため
柱の破壊モードは曲げ破壊型である
④ 当該柱の種別を、昭和55年建設省告示第1792号(以下、「告示」という。)に従って判定し、種別判定の根拠を簡潔に記述せよ。
答え
[ 解答解説 ]
③よりせん断破壊は生じないため、付着割裂破壊が生じないことを前提とすると
ho/D = 3000mm/700mm = 4.29 ≧ 2.5・・・FAの条件を満足
σo /Fc=8. 900N/mm2/24N/mm2 = 0.371
0. 35 < σo /Fc ≦ 0. 45 ・・・・FBの条件を満足
pt = 0.517% ≦ 0.8% ・・・・・・FAの条件を満足
τu /Fc = ( 999000N / 700mm / 700mm) / 24N/mm2=0. 0849 ≦ 0. 1・・・・FAの条件を満足
(τuは柱の曲げ破壊時せん断力による)
より、σo /Fc のみがFAとなる条件の0.35以下を満足していないため
当該柱の部材種別はFBである
[ No.2 ]
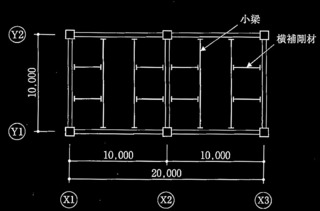
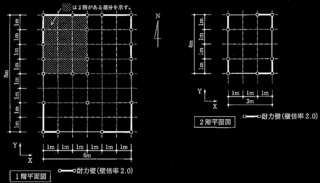
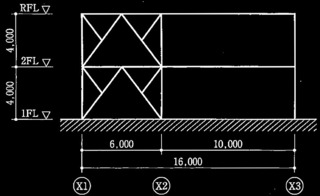
表2に示す鉄筋コンクリート造地上3階建ての建築物を対象に静的非線形荷重増分解析(以下、「増分解析」という。)を実施して保有水平耐力を計算した。次の①~④の設問に解答せよ。なお、計算対象はX方向とし、構造形式は耐力壁付きラーメン構造とする。
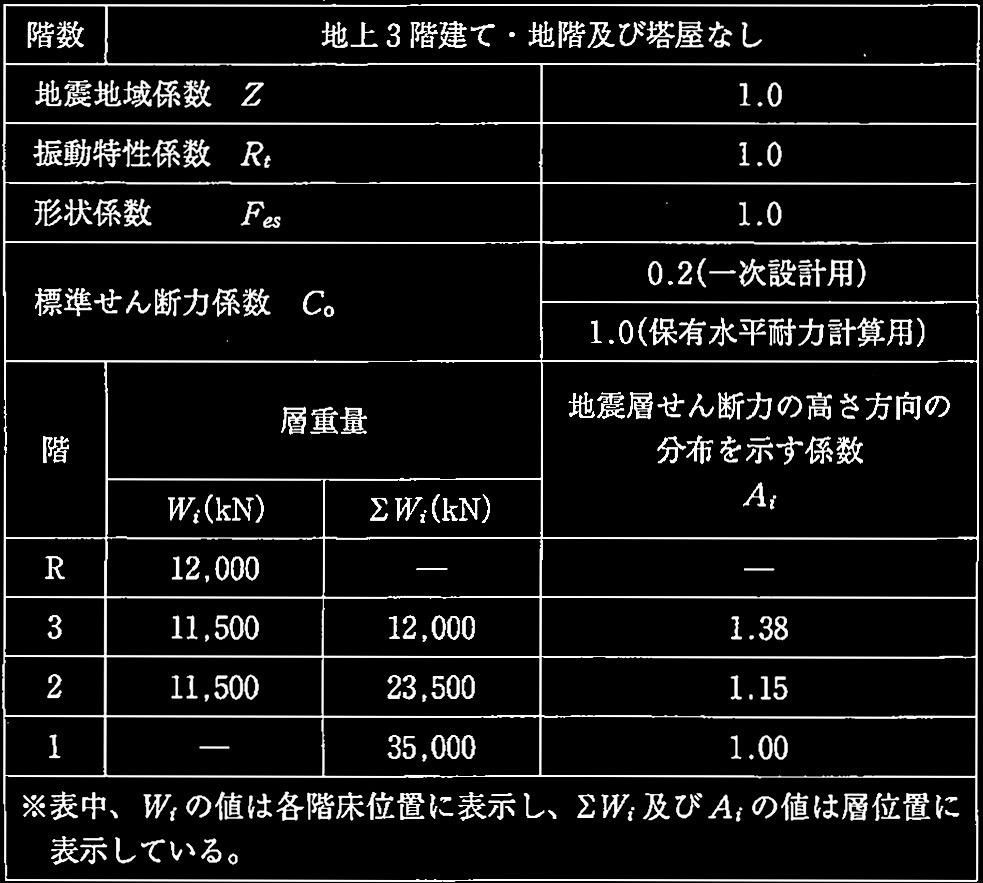
表2 対象建築物の構造計算に用いる諸元
く増分解析 保有水平耐力の計算に用いた条件及び計算結果等>
(a) 増分解析の地震力分布には、建築基準関係規定に規定する一次設計用地震力の分布を用いた。
(b) 架構は、増分解析時に脆性破壊することなく、増分解析終了時には全体崩壊形を形成した。
(c) 保有水平耐力は、増分解析終了時の水平耐力とした。
(d) 3階の保有水平耐力は 6,955kNで、柱及び耐力壁の負担水平耐力は下記のとおりであった。
種別FAの柱が負担する水平耐力の合計は 1,850 kN
種別FBの柱が負担する水平耐力の合計は 1,050 kN
種別FCの柱が負担する水平耐力の合計は 355kN
耐力壁の種別は全てWAで、負担する水平耐力の合計は 3,700kN
(e) 必要保有水平耐力は、建築基準関係規定に基づき計算した。
① 1階の保有水平耐力(Qu1)を求めよ。なお、Qu1の単位は kNとし、小数第1位を四捨五入して表記せよ。
答え
[ 解答解説 ]
保有水平耐力を算出した増分解析は一時設計用地震荷重の分布を用いているため、3階の保有水平耐力が6955kNより、1階の保有水平耐力は
Qu1= ΣW1 × A1× (6955 kN/ ΣW3 × A3)
= 35000kN×1.00 × (6955kN/12000kN/1.38)
Qu1= 14700 kN
② 3階柱の部材群としての種別を告示に従って判定し、種別判定の根拠を簡潔に記述せよ。
答え
[ 解答解説 ]
γA= 1850kN/ (1850kN + 1050kN +355kN)
= 0.568
γC= 355kN/ (1850kN + 1050kN + 355kN)
= 0.109
より
γA ≧ 0.5かつ γC ≦ 0.2
のため
3階柱の部材群としての種別はAである
③ 3階の構造特性係数(DS3)を告示に従って算定し、算定の根拠を簡潔に記述せよ。
答え
[ 解答解説 ]
耐震壁の部材種別は全てWAである
耐震壁の負担水平力の割合βuは、3700kN / 6955kN=0.532
であり
0.3 < βu ≦ 0.7となっている
②より柱はりの部材群としての種別はA
以上より3階の構造特性係数Dsは、0.35である
④ 1階の構造特性係数(DS1)は3階より 0.05 大きい値であった(DS1= DS3 + 0.05)。 1階の必要保有水平耐力(Qun1)に対する1階の保有水平耐カ(Qu1)の比率(Qu1/Qun1)を求めよ。
答え
[ 解答解説 ]
1階の構造特性係数DS1=DS3 + 0.05 = 0.35+0.05 = 0.40
よって1階の必要保有水平耐力Qun1は
Qun1=DS1 × Z × Rt × Fes × Σ W1 × A1
=0.40 × 1.0 × 1.0 × 1.0 × 35000kN × 1.00
= 14000kN
Qu1/Qun1= 14700kN/14000kN= 1.05
[ No.3 ]
次の枠内の文章は、鉄筋コンクリート造8階建てラーメン構造の建築物に対して、増分解析により保有水平耐力を確認したときの構造設計者の総合所見である。この文章中の二重下線部分について、この対応が適切か、不適切かを答えよ。
不適切とした場合には、最も適切と考えられる対応を簡潔に記述せよ。なお、ここでは、ある荷重ステップにおける各層の層間変形角の最大値を最大層間変形角としている。
架構の水平耐力が必要保有水平耐力を上回る層間変形角の設計目標を1/100としたため、各階の保有水平耐力は最大層間変形角が1/100時点における層せん断力とした。
部材の種別は、同じ変形時点(最大層間変形角が1/100時点)の応力を用いて判定して、各階の必要保有水平耐力を計算した。
答え
[ 解答解説 ]
【 部材の種別は、同じ変形時点(最大層間変形角が1/100時点)の応力を用いて判定して、各階の必要保有水平耐力を計算した。】は不適切である。
部材の種別を算定する際の応力は崩壊形が確認された時点の応力を用いるべきであるため、全体崩壊形が形成された1/40時点の応力を用いて部材の種別を算定すべきである。
この記事へのトラックバックURL
https://fanblogs.jp/tb/12618320
※ブログオーナーが承認したトラックバックのみ表示されます。