2024年09月26日
令和五年度修了考査 構造設計(記述式)問題1
問題1
次の直接基礎(独立フーチング基礎)の設計に関する設問 [ No.1 ] 及び杭基礎の鉛直支持力等に関する設問 [ No.2 ] について解答せよ。
[ No.1 ]
次に示す硬質粘土地盤を支持層とする直接基礎(独立フーチング基礎)で設計する場合の長期許容鉛直支持力及び即時沈下量の検討に関する次の①~⑤の設問について解答せよ。
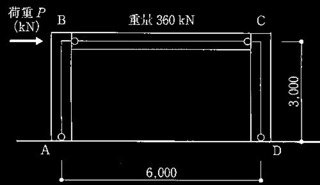
く検討の対象とする独立フーチング基礎の概要>
長期鉛直荷重 W: 700kN(フーチング自重含む、荷重の偏心及び傾斜なし)
底版形状 :正方形(2m × 2m)
く支持地盤の概要•地盤係数等>
土 質 :洪積粘性土
一軸圧縮強さqu :200 kN/m2
地盤のヤング係数Es:15,000 kN/m2
地盤のポアソン比Vs : 0.4
単位体積重量γ : 16kN/m3
地下水位 : GL-2.0m
① 地盤の長期許容鉛直支持力qαLを式(1)により求めよ。ただし、根入れの影響は無視する。
答え
[ 解答解説 ]
解答例中で計算結果を表示する場合は、途中表示も含めて有効数字3桁とする。
qαL =1/3 ×( a•c•Nc + β•γ1•B•Nγ + γ2•Df•Nq ) ・・・式(1)
支持地盤の土質が粘性土であることから内部摩擦角φ= 0.0° なので、
表1よりNc= 5.10、Nγ = 0.0、Nq= 1.00となる。
底版形状は 2m × 2mなので
B = 2.00、L = 2.00より
α= 1.0 + 0.2×(2/2) = 1.2
問題文より c = qu/2 = 200/2 = 100(kN/m2)となり、
α•c•Nc = 1.20•100•5.10 = 612(kN/m2)
β•γ1•B•Nγ = 0.0(kN/m2)
また問題文中に「根入れの影響は無視する」とあるので、
Df = 0.0であり、
γ2•Df•Nq = 0.0(kN/m2)
したがって式(1)より算定される地盤の長期許容鉛直支持力は、
qαL = 1/3 ×( a•c•Nc + β•γ1•B•Nγ + γ2•Df•Nq )
= 1/3 ×( 612 + 0.0 + 0.0 )
= 204(kN/m2)
② 検討の対象とする独立フーチング基礎の長期接地圧p(基礎底版に作用する単位面積当たりの荷重)を求めよ。
答え
[ 解答解説 ]
長期接地圧pは、長期鉛直荷重Wを底版面積Afで除して求める。
底板形状は2m × 2mなので、
Af = 2.00 X 2.00 = 4.00(m2)
したがって
p = w/Af = 700/4.00 = 175(kN/m2)
③ 長期許容鉛直支持力qαLと長期接地圧Pの比較により、支持地盤の安全性を検証せよ。
qαL =1/3・( a•c•Nc + β•γ1•B•Nγ + γ2•Df•Nq ) ・・・式(1)
qαL:長期許容鉛直支持力(kN/m2)
α,β:基礎の形状係数で、長方形基礎(短辺B、長辺L)の場合には、
α = 1.0+ 0.2B/L、β= 0.5 - 0.2B/L
Nc、Nγ、Nq:支持力係数(表1参照)
c:支持地盤の粘着力(kN/m2)(c = qu /2としてよい)
γ1:支持地盤の単位体積重量(kN/m3)
γ2:根入れ部分の土の単位体積重量(kN/m3)
Df :根入れ深さ(m)
表1 支持力係数

(日本建築学会:建築基礎構造設計指針より)
答え
[ 解答解説 ]
p = 175 < qαL = 204より、
長期許容鉛直支持力が長期接地圧を上回っていることから、支持地盤の安全性に問題はない。
④ 検討の対象とする独立フーチング基礎の即時沈下量 SEを式(2)により求めよ。
答え
[ 解答解説 ]
SE = Is•( 1 – νs2) / Es・p•B ・・・式(2)
基礎の剛性は∞と考え、底面形状は正方形であることから、表2より、
ls= 0.88
また、vs = 0.40, Es = 15000(kN/m2), p = 175(kN/m2), B = 2.00(m)より
SE = Is•( 1 – νs2)/ Es・p•B
= 0.88•(1-0.402)/15000・175・2.00
= 0.0172(m)
⑤ 算出した即時沈下最SEより、独立フーチング基礎に対する安全性を検証せよ。ただし、十分に剛性のある基礎を想定する。また、本建築物の即時沈下の総沈下醤の限界値は20mmとする。
SE = ls•(1-νs2)/Es × p •B ・・・式(2)
SE :即時沈下量(m)
ls:基礎底面の形状と剛性によって決まる沈下係数で、表2による。
νs :地盤のポアソン比
Es:地盤のヤング係数(kN/m2)
p:長期接地圧(kN/m2)
B:基礎の短辺長さ(m)
L:基礎の長辺長さ(m)
表2 沈下係数
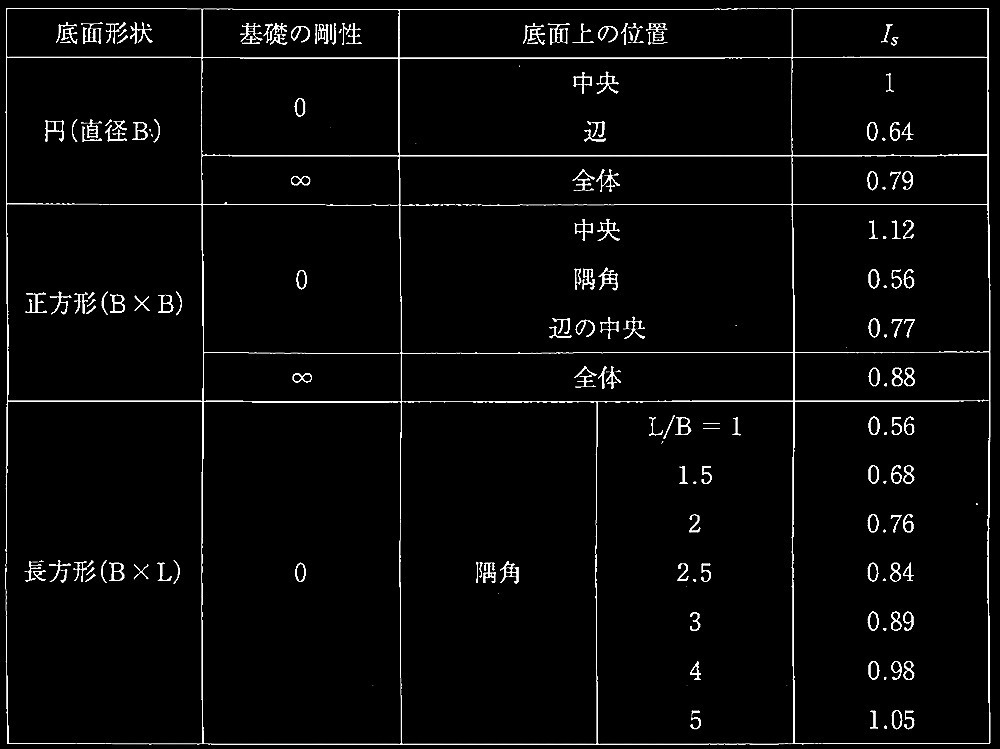
(日本建築学会:建築基礎構造設計指針より)
答え
[ 解答解説 ]
問題文に「十分に剛性のある基礎と想定する」とあるので、
④で考えた通り、SE = 0.0172(m)=17.2(mm)である。
したがってSE=17.2(mm)< 本建物の即時沈下量の限界値=20(mm)
より、算定した即時沈下量は限界値を下回っていることから、
安全性に問題はない。
[ No.2 ]
図1のような地盤に、杭頭をGL-2.0 m、杭先端をGL-23.0mとした場所打ち鉄筋コンクリート拡底杭(軸径2.0m、杭先端有効径3.0m)を造成する場合の杭の鉛直支持力等に関する次の①~⑤の設問について解答せよ。ただし、杭の長期許容鉛直支持力の算定には式(3)を用いるものとし、拡底部の周面摩擦抵抗力は考慮しないものとする。
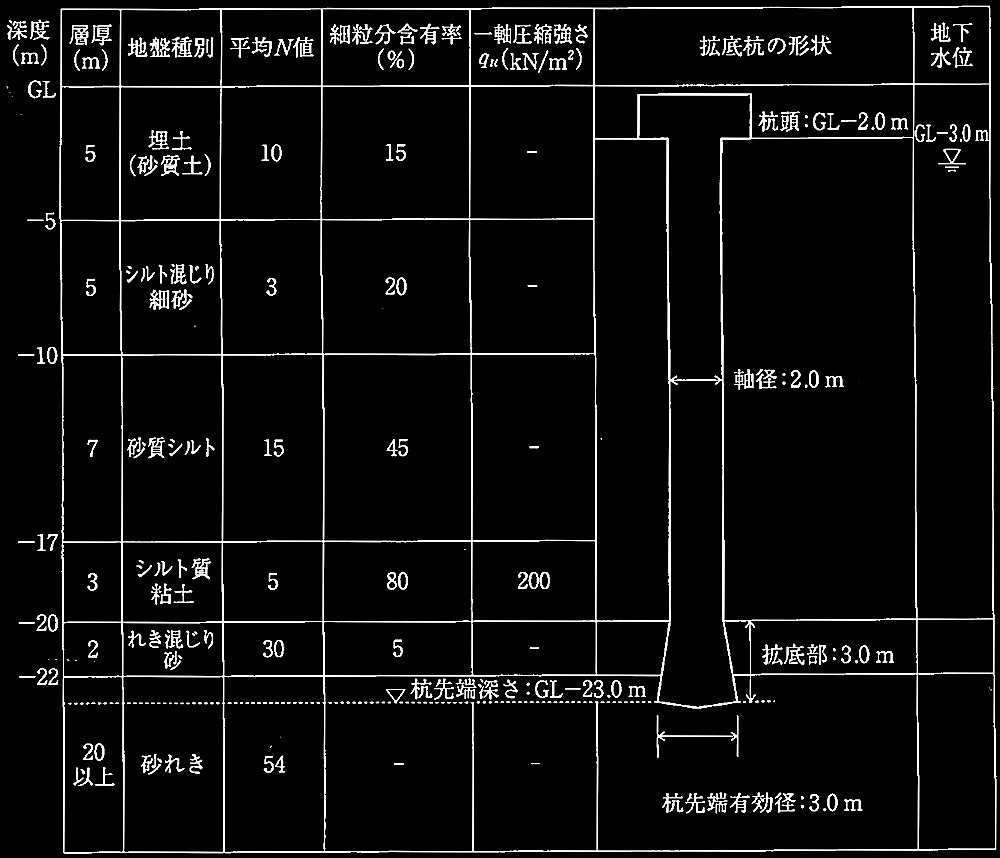
図1 地盤構成及び杭の概要
RαL = 1/3 × (Rp + Rf ) ・・・式(3)
RαL:杭の長期許容鉛直支持力(kN)
Rp:極限先端抵抗力(kN)で、Rp = 100・N・Ap
ただし、100Nの上限を7,500とする。
N:杭先端から下に1dp(dpは杭先端有効径)、上に1dp間の平均N値
Ap:杭の先端面積(m2)
Rf:極限周面摩擦抵抗力(kN)で、Rf = Rfs + Rfc
Rfs:砂質土層の極限周面磨擦抵抗力(kN)で、Rfs = Σ3.3•Ns•Ls•ψ
Ns:砂質土層の杭周面のN値で、上限を50とする。
Ls:砂質土層の長さ(m)
ψ:杭の周長(m)
Rfc:粘土層の極限周面摩擦抵抗力(kN)
Rfc = Σ(1/2•qu•Lc•ψ)
qu:粘土層の杭周面の一軸圧縮強さ(kN/m2)で、上限を200とする。
Lc:粘土層の長さ(m)
①杭の極限先端抵抗力Rpを求めよ。
答え
[ 解答解説 ]
問題文より杭先端有効径 dp = 3.00(m)であることから、
N = (1/6)× (30.0 + 30.0 + 54.0 + 54.0 × 3) = 46.0
100•N = 100•46.0 = 4600 < 7500
AP = 1.50 × 1.50 × π = 7.07(m2)
以上より、杭の極限先端抵抗力は
Rp = 100•N•AP = 4600•7.07
= 32500(kN)
② 当該地盤において、液状化の検討を必要とするすべての地盤種別を挙げ、その理由を3つ述べよ。
答え
[ 解答解説 ]
2020年版建築物の構造関係技術基準解説書P.562より液状化のおそれのある地盤は、次に該当するような砂質地盤とされている。
・地表面から20m以内の深さにあること
・砂質土で粒径が比較的均ーな中粒砂等からなること
・地下水で飽和していること
・N値が概ね15以下であること
そこで液状化の検討を必要とする地盤種別は次の2つ、
・埋土(砂質土)
・シルト混じり細砂
とし、その理由は以下の3つとする。
(1) 地表面から20m以内の深さにある
(2) 地下水で飽和した砂質土である
(3) N値が15以下である
③ 液状化判定の結果、GL–10 mより浅い埋土層及びシルト混じり細砂層は、液状化の可能性が高いことが判明した。その結果を考慮し地震直後にも長期の安定性を確保することを目標にして、当該地盤における砂質シルト土層の極限周面摩擦抵抗力Rfsを求めよ。
答え
[ 解答解説 ]
砂質シルト層について、
Ns = 15.0、Ls = 7.00(m)、ψ= 2.00 × π=6.28(m)より、
Rfs =Σ3.3•Ns•Ls•ψ
= 3.3•15.0•7.00•6.28
= 2180(kN)
④ 当該地盤におけるシルト質粘土層の極限周面摩擦抵抗力Rfcを求めよ。
答え
[ 解答解説 ]
シルト質粘士層について、
qu=200(kN/m2)、Lc= 3.00(m), ψ = 6.28(m)より、
Rfc = Σ( 1/2•qu•Lc•ψ)
= 1/2•200•3.00•6.28
= 1880(kN)
⑤ 以上より、杭の長期許容鉛直支持力RαLを求めよ。
答え
[ 解答解説 ]
RαL = (1/3)×(Rp +Rf) ・・・式(3)
①よりRp = 32500(kN)
③よりRfs = 2180(kN)
ここで、液状化層の扱いは長期の安定性に配慮し、GL-10m以浅の周面摩擦抵抗力は無視した。
④と問題文中「拡底部の周面摩擦抵抗力は考慮しない」とあるので、Rfc = 1880(kN)
よって
Rf = Rfs + Rfc
= 2180 + 1880 = 4060(kN)
したがって、杭の長期許容鉛直支持力Rは
RαL = (1/3)×(Rp +Rf)
= (1/3)×(32500 + 4060)
= 12200(kN)
この記事へのトラックバックURL
https://fanblogs.jp/tb/12718178
※ブログオーナーが承認したトラックバックのみ表示されます。