令和二年度修了考査法適合確認問題５: 構造設計一級建築士とらの巻

<< 令和元年度修了考査構造設計（4肢択一式）　No.1 ～ No.10 | TOP | 令和二年度修了考査法適合確認問題４ >>

2024年08月05日

令和二年度修了考査法適合確認問題５

問題５
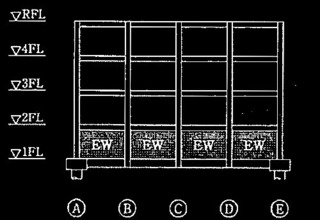
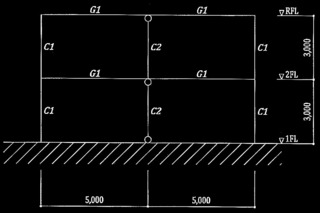
在来軸組工法による木造2階建て住宅の、地震力に対する耐力壁の設計に関する以下の設問に解答せよ。対象とする建築物の概要は以下に示すとおりで、図1に南側概略立面図を、図2に各階平面図を示す。図2中の太線部分は耐力壁を示しており、実線は壁の倍率 2.0、破線は壁の倍率1.0である。また、図2中に示したX、Yの矢印は地震時の水平力の加力方向を示している。

く建築物概要＞
　用　　途　専用住宅
　規　　模　地上2階建て（小屋裏の利用なし）
　延べ面積　116m²（1階：68m², 2階：48m²）
　構　　造　在来軸組工法による木造
　　　　　　軒の高さ：6.1m、
　　　　　　最高高さ：7.3m、
　　　　　　階　　高：1階及び2階ともに2.8m
　仕上げ　　屋根：瓦葺
　　　　　　外壁：サイデイングボード張り
　建設地　　多雪区域の指定のない区域（垂直積雪量：30cm)　　
　地　　盤　長期許容応力度：50kN/m²
　その他　　野地板及び床板：構造用合板直張り（いわゆる、剛床仕様）

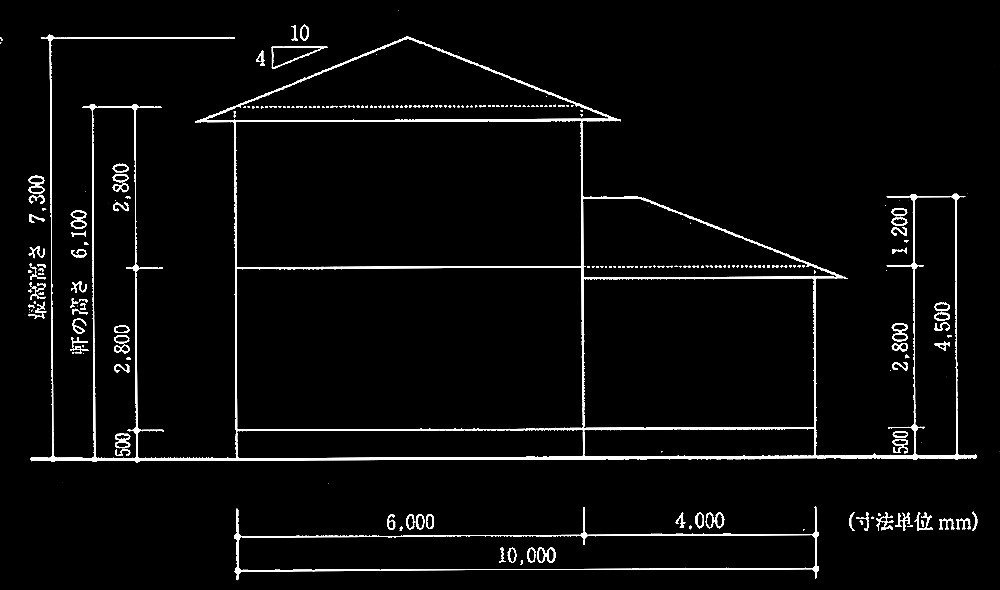
R02_1_問題5_図1_南側概略立面図.jpg

図1 南側概略立面図

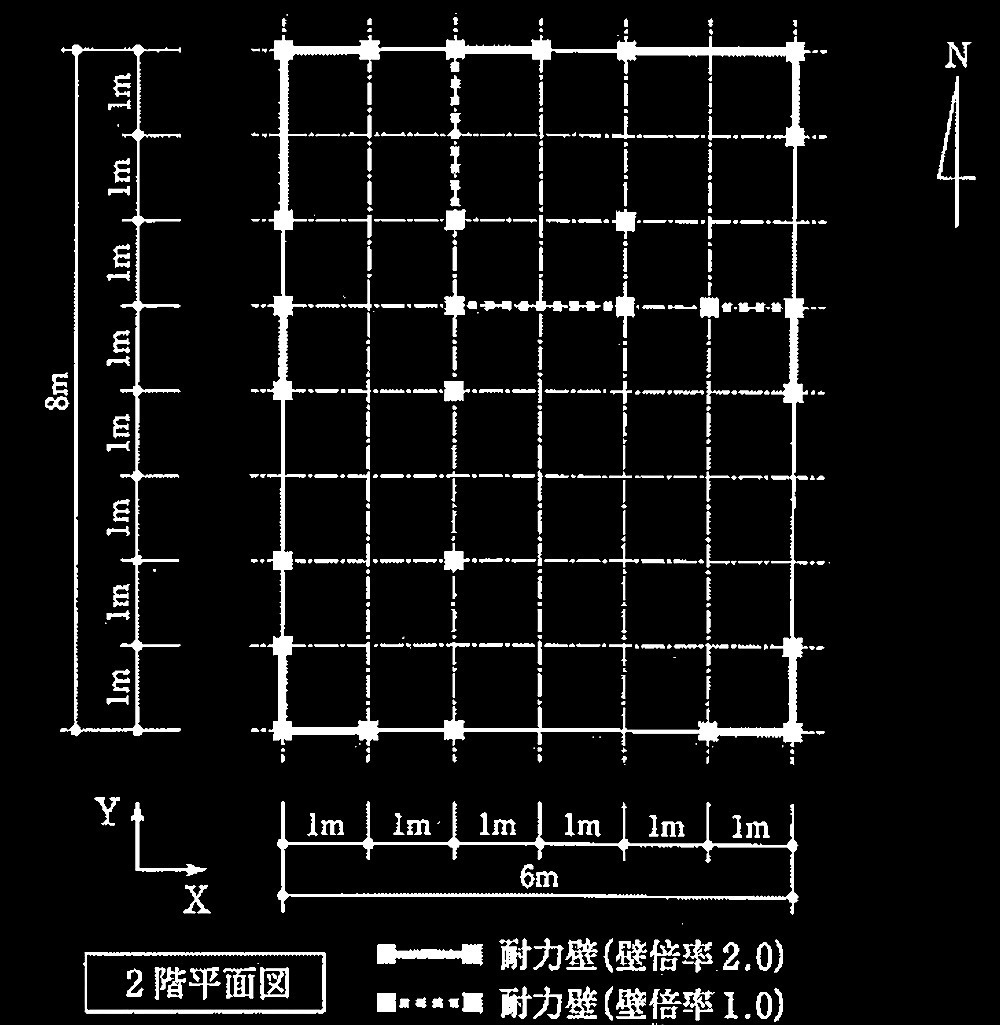
R02_1_問題5_図2_2階平面図.jpg

図2 各階平面図

表1 地震力用必要壁率 (m/m²）
R02_1_問題5_表1_地震力用必要壁率.jpg

[No.1]
この建築物の地震力に対する検討を、建築基準法施行令第46条の規定（いわゆる壁量計算）により行う場合について、以下の①及び②の設問に解答せよ。

①地震力に対する1階のX、Y方向の壁量が適合しているか否かを判定せよ。なお、地震力用必要壁率は、表1に示すとおりとする。

答え

[ 解答解説 ]
1階床面積
A= 10.0 × 5.0 + 6.0 × 3.0= 68.0m²

屋根仕上が瓦葺のため、地震力用必要壁率は重い屋根で算定する。

必要壁量 Lu= 68.0m² × 0.33m/m²= 22.44m
X方向壁量
Lwx = (2.0m × 3枚 +1.0m × 6枚) × 2.0倍 + (2.0m + 1.0m) × 1.0倍
　　= 27.0m > 22.44m
　∴　OK
Y方向壁量
Lwy = (2.0m × 2枚 + 1.0m × 4枚) × 2.0倍 + (2.0m × 2枚 + 1.0m × 3枚) × 1.0倍
　　＝23.0m　> 22.44m
　∴　OK
以上より、地震力による壁量は1階は、X方向、Y方向共に適合している。

②四分割法により1階のX、Y方向の耐力壁配置が適合しているかを判定せよ。

答え

[ 解答解説 ]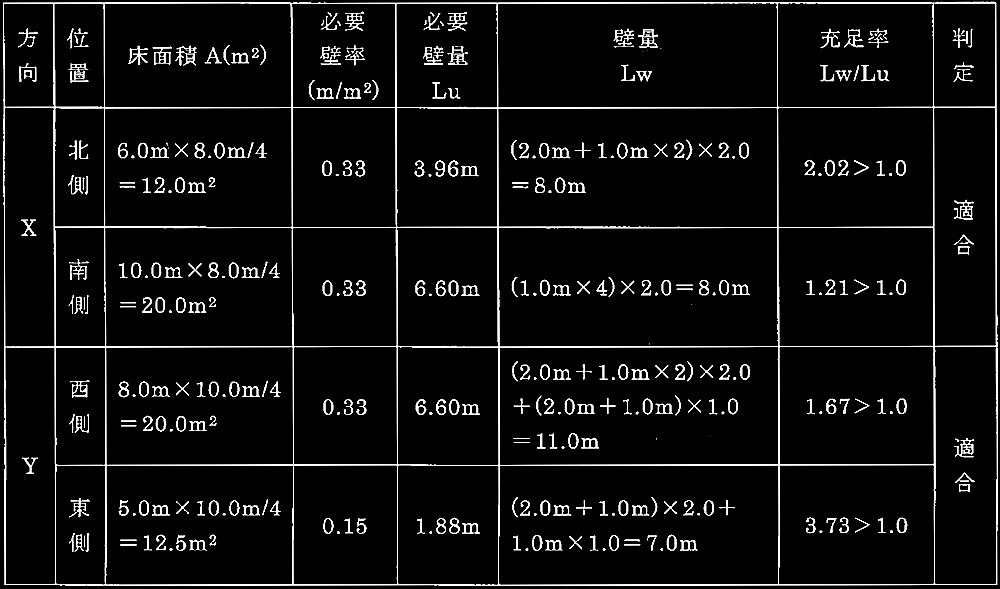
R02_1_問題5_No.1_壁量計算.jpg

以上より、X・Y方向共に充足率が1.0を超えているため、壁率比に係わらず壁の配置は適合している。

[ No.2 ]
この建築物の地震力に対する耐力壁の検討を、許容応力度計算（構造計算）により行う場合について、以下の①及び②の設問に解答せよ。

①振動特性係数Rtを算出する際に用いる設計用1次固有周期Tを、昭和55年建設省告示第1793号第2に示された式により求めよ。なお、建築物の高さは、軒の高さと最高高さの平均値を用いるものとする。

答え

[ 解答解説 ]
建築物の高さ
　H= (7,300+ 6,100)/2= 6,700mm→6.70m
設計用一次固有周期
　T= 6.70 × (0.02 + 0.01 × 1.0)=0.201秒

② 表2は地震力に対する安全性の検討を行ったものである。空欄(ｱ)～(ｴ)に数値を記入し、判定欄の「適合」、「不適合」のいずれかを選べ。なお、表2は次の条件によるものとする。

1) 地震層せん断力係数 Ciは、Z =1.0、Rt =1.0、Co =0.2として算定している。
2) 壁倍率1.0の耐力壁の許容せん断耐力は、1.96 kN/mとして算定する。
3) ΣEQi は設計用せん断力を、ΣEPi は許容せん断耐力を表す。

表2 地震力に対する耐力壁の検討
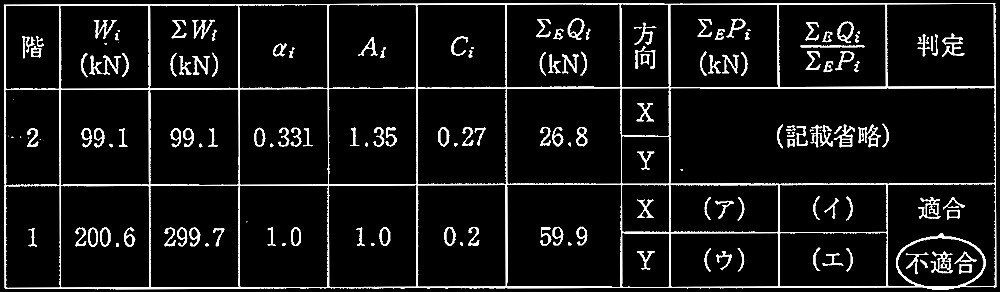
R02_1_問題5_NO.2_表2_地震力に対する耐力壁の検討.jpg

答え

[ 解答解説 ]
(ｱ) X方向 ΣEPi = 27.0m × 1.96kN/m = 52.92 kN
(ｲ) X方向 ΣEQi /ΣEPi = 59.9/52.92 = 1.13 > 1.00 NG
(ｳ) Y方向 ΣEPi = 23.0m × 1.96kN/m = 45.08 kN
(ｴ) Y方向 ΣEQi /ΣEPi = 59.9/45.08 = 1.33 > 1.00 NG

以上より、X・Y方向共に地震力に対する耐力壁の検討は不適合である。

[ No.3 ]
木造建築物の地震力に対する検討を、設問 [ No.1 ]のような壁量計算による方法と、設問 [ No.2 ] のような許容応力度計算による方法で行った場合とでは、得られる判定結果（適合か不適合）が異なることもある。判定結果が異なる要因について述べ、木造建築物の設計に当たり、構造設計者としてどのように対応すべきかを簡潔に述べよ。

答え

[ 解答解説 ]
基準法の壁率が想定している建築物の重量より、最近の建築物重量は重い傾向があり、壁量計算が適合であっても詳細に建築物の重量を積算する許容応力度計算では不適合になる場合があるので、壁量計算による場合は余裕をもった壁量を確保する必要がある。