構造設計一級建築士 とらの巻

問題２
鉄筋コンクリート造建築物の耐震計算ルート3による設計に関する以下の設問に解答せよ。

[ No.1 ]
鉄筋コンクリート梁の種別の判定に関する以下の�@〜�Bの設問に解答せよ。なお、対象とする梁（以下、「当該梁」という。）の諸元は図l、図2及び表1によるものとし、当該梁の種別判定では、接着する柱の種別は考慮しないものとする。


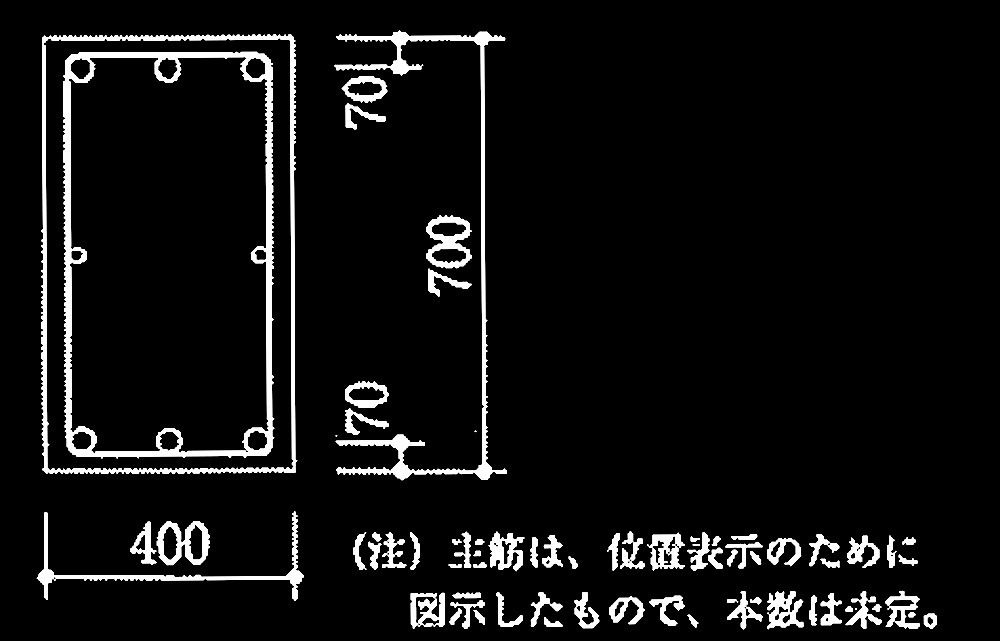
図1 梁断面 （単位：mm)


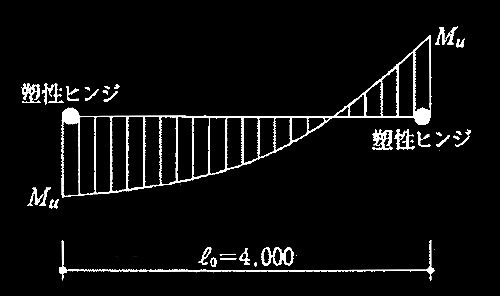
図2 梁の曲げ破壊時曲げモーメント分布 （単位：mm）


表1 当該梁の諸元（計算に用いる値）



【その他の諸条件】
(a) 梁の曲げ破壊時せん断力Qmuは、長期せん断力Qo、及び塑性ヒンジ発生時せん断力QMを用いて式（1）により算定する。ここで、QMは両端の曲げ終局モーメントMuの和を内法長さ ℓo で除した値とする。なお、床スラブの寄与は無視し、左端のMuと右端のMuは等しいものとする。

　　Qmu = Qo + QM　　　　式(1)
ここに、QM = 2Mu/ℓo


(b) 梁の破壊モードは、梁のせん断終局耐力Qsuが式(2)を満足する場合には曲げ破壊（構造耐力上支障のある急激な耐力の低下のおそれがない。）とし、満足しない場合にはそれ以外の破壊（構造耐力上支障のある急激な耐力の低下のおそれがある。）とする。なお、付着の検討は別途行われているものとする。

　　Qsu ≧ Qo + 1.1QM　　　式(2)

�@ 当該梁の耐力等が次のように与えられる場合、当該梁の種別を昭和55年建設省告示第1792号に従って判定し、種別判定の根拠を簡潔に記述せよ。

【 耐力等の条件 】
　長期せん断力　　　　　　　Qo = 0.020Fcbj
　塑性ヒンジ発生時せん断力　QM = 0.035Fcbj
　せん断終局耐力　　　　　　Qsu = 0.062Fcbj

答え

[ 解答解説 ]
�@ Qo + 1.1QM = (0. 020+1.1 × 0.035) Fcbj = 0.0585 Fcbj (kN)
　　∴τu/Fc = 0.0585 ≦ 0.15

　 Qsu = 0. 062 Fcbj
　　∴ Qsu ≧ Qo + 1.1QM
以上よりこの梁の種別はFAとなる。

�A 当該梁のせん断終局耐力Qsuが�@の条件、Qsu = 0.062Fcbjとなるあばら筋の最小間隔を求めよ。梁のせん断終局耐力の算定式は式(3)によるものとする。

答え

[ 解答解説 ]
�A「ただし、・・・」以下より式（3）は以下となる
　Qsu = (0. 78 + 0. 85√(pw・σwy)) bj (kN)

そして、Qsu ≧ 0. 062 Fcbjより
　(0.78+0.85√(pw・σwy) bj ≧ 0.062 Fcbj = 1.488 bj
0. 85√(pw・295) ≧ 0.708
pw ≧ (0.708 / 0.85)^ 2/295=0.00235

最小間隔を＠とすると pw = 2 × 71/ b @≧0.00235
∴ ＠ 151.1 (mm)

�B 当該梁の種別がFDとなる引張主筋の最小本数を求めよ。その際、梁の曲げ終局モーメントMuは式(4)によるものとする。また、Qo及びQsuは�@の［耐力等の条件 ] と同じ値とする。なお、主筋は一段筋とし、スラブ筋の寄与は無視する。

答え

[ 解答解説 ]
�B Qo, Qsuの値が�@の耐力の条件と同じという事からFDとなるためには剪断破壊することが条件となる。
つまり、Qsu < Qo + 1.1QMとなることが条件となる。

QM > ((Qsu-Qo) /1.1) = ( 0.062 - 0.020 ) Fcb j /1.1=201966. 5N=202.0kN

QM=2Mu/ℓoなので、2Mu/ℓo> 202.0kN
∴　Mu > 202 × 4.0/2=404 kNm

上式と式(4)より
at = 404・10⁶ / (0.9sσyd) =1899 mm²
∴　4-D25 (2028 mm²）

●確認
Mu = 0.9・507・4・429・551/106=431
QM = 431・2/ 4.00=216
Qo = 0.020・24・400・551/10³ = 106
Qo + 1.1QM = 106 + 1.1・216 = 344
Qsu = 0.062・24・400・551/103=328

[ No.2 ]
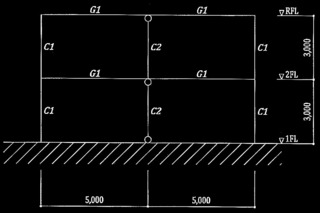
図3に示す鉄筋コンクリート造純ラーメン架構を対象に、非線形静的荷重増分解析（以下、「増分解析」という。）を実施して、保有水平耐力を計算した。図中の3箇所の1階柱（イ柱、ロ柱、ハ柱）について、以下の�@〜�Bの設問に解答せよ。


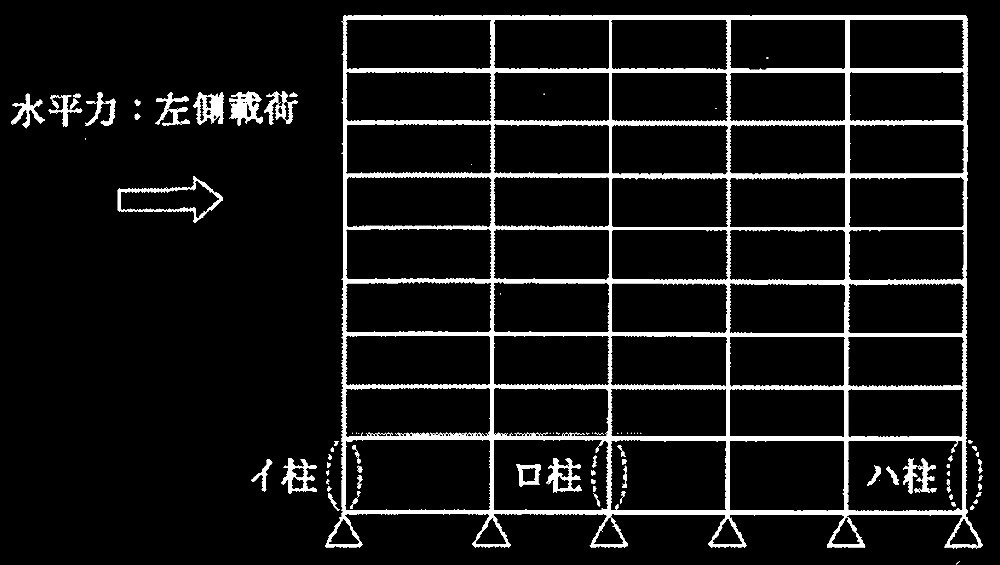
図3 解析対象の架構（純ラーメン構造）


【増分解析の条件及び解析結果】
(a) 増分解析の水平力は、一次設計用地震力の分布とし、図3に示すように左側から載荷した。

(b) 部材はせん断に対しては弾性とした。

(c) 増分解析では、柱の軸方向力Nと曲げ終局モーメントMuとの相関関係（N-Mu関係）を考慮した。図4に、3箇所の1階柱（A柱、B柱、C柱）の柱脚について、N-Mu関係は同一として増分解析の各ステップにおける軌跡をそれぞれ示す。なお、軸方向力は圧縮を正、引張を負とし、図中の括弧内の値は、該当ステップ時の軸方向力Nと柱脚曲げモーメントMaである。

(d) 増分解析終了時には、崩壊形を形成した。なお、 1階柱脚が曲げ破壊したが、 1階柱頭は曲げ破壊しなかった。

(e) 柱の破壊モードは、柱のせん断終局耐力Qsuが式（5）を満足する場合には曲げ破壊、満足しない場合にはせん断破壊とする。ここでは、 1階柱の柱脚塑性ヒンジ発生時せん断力QMは、式(6)による。その際、1階柱の曲げモーメントの反曲点高さは、図5に示すように 2/3 ho（ho：柱の内法高さ）とする。

　Qsu ≧ 1.25QM　　　式(5)
　QM =1.5Mu/ho　　　式(6)



図4 柱の軸方向力Nと曲げ終局モーメントMuとの相関関係


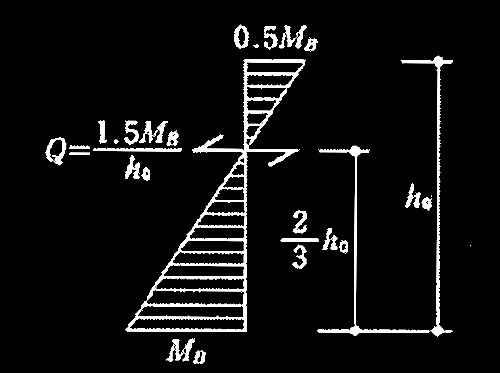
図5 1階柱の曲げモーメント分布


�@ 図4に示したA柱、B柱、C柱の軌跡は、それぞれ、図3のイ柱、口柱、ハ柱のどの柱に該当するかを推定し、その根拠を簡潔に記述せよ。

答え

[ 解答解説 ]
�@
A柱：ハ柱 、軸力が次第に増加しているため
B柱：口柱 、軸力に変動がすくないため
C柱：イ柱 、軸力が次第に減少して最終的には引張になっているため

�A 3箇所の1階柱（A柱、B柱、C柱）の破壊モードを曲げ破壊とするために必要なせん断終局耐力の下限値minQsuについて、下記の空欄に該当する数値を記入せよ。その際、柱のせん断終局耐力Qsuは軸方向力の変動に関わらず一定としてよい。

　A柱のせん断終局耐力の下限値 minQsu = [　　] Mo/ho
　B柱のせん断終局耐力の下限値 minQsu = [　　] Mo/ho
　C柱のせん断終局耐力の下限値 minQsu = [　　] Mo/ho

答え

[ 解答解説 ]
�A
技術基準解説書では、Ds算定時と保有水平耐力時に対する保証設計を行うこととしている。ここでは荷重増分解析中におけるM-N相関関係で最も不利な状況に対する検討とする。

A柱：1.5 × 1.00 × 1.25 = 1.88
B柱：1.5 × 0.80 × 1.25 = 1.50
C柱：1.5 × 0.60 × 1.25 = 1.13

�B 3箇所の1階柱（A柱、B柱、C柱）のうち、地震時に小さな変形において耐力低下が生じることが最も危惧されるのはどの柱か推定し、その根拠を簡潔に記述せよ。また、耐力低下を防止する対策として最も有効と考えられる方法を一つ簡潔に述べよ。

答え

[ 解答解説 ]
�B
変形が小さい場合でも軸力比が大きい（ Nu/No = 0.53 > 0.40）Aの柱が圧縮側コンクリートの圧壊によって耐力低下が生じやすい。

対策としては、帯筋を溶接型やスパイラル型にし、閉鎖型の副帯筋を用いてコアコンクリートを拘束する。また、帯筋や副帯筋を密にして主筋の座屈を防止する。