両端で減衰する関数
前回に引き続いて無理関数です。まずは比較的シンプルなものから:
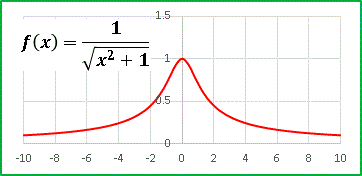
f(0) = 1 を頂点とする左右対称の山なりの関数です。
y = 1/x に近い勾配をもつ曲線ですが、分母は必ず正値をとるので x = 0 で定義されつつ滑らかに連結されています。この関数に三角関数を掛けてみましょう。
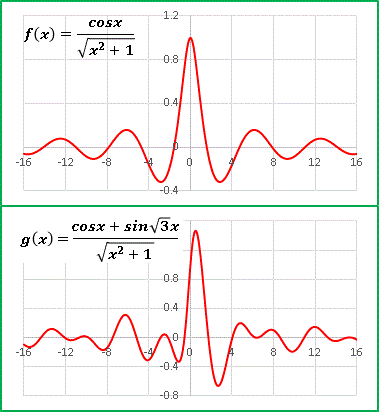
f(x) は原点にピークを持ち、両端で減衰していく関数。
g(x) は概周期関数ですから周期は崩れてしまっています。
しかし x → ±∞ で 0 に収束することには変わりありません。
周期的に滑らかでない点が現れます
次は 1 + sin[pi*x]と、その平方根をとった関数です:![03[1+sinπx]平方根.gif](/excelmathfunction/file/035B12BsinCF80x5DE5B9B3E696B9E6A0B9.gif)
f(x) は全域で滑らかな関数ですが、g(x) は x = 1.5, 3.5, 5.5, …… という滑らかではない点が周期的に現れます。滑らかではないというのはつまり、その点で微分が定義できないということです。g(x) を微分してみると
となりますね。g(x) がそのまま分母に入っていますから、 x = 1.5, 3.5, 5.5, …… でこの関数を定義することはできません。
y = 1 と同等なグラフ?
次は分母・分子が共に2次関数の平方根という例:![04[2次関数/2次関数]平方根①.gif](/excelmathfunction/file/045BEFBC92E6ACA1E996A2E695B0EFBC8FEFBC92E6ACA1E996A2E695B05DE5B9B3E696B9E6A0B9E291A0.gif)
x が大きい領域では f(x) ≒ 1 とみなすことができます。つまり直線 y = 1 とほぼ同等なグラフと考えることができます。乱暴なようですが x → ±∞ では厳密にこれが成り立ちます。
f(x) に cos[pi*x] を掛けた関数が g(x)です。原点付近で少し荒い動きをしますが、x が大きい領域では普通の三角関数として振る舞います。
g(x) において分子を4次関数の平方根としたのが h(x) です。振幅は原点から2次関数的に増加していくことになります。
最後に g(x) の分子を指数関数の平方根で置き換えてみます:
![05[2次関数/2次関数]平方根②.gif](/excelmathfunction/file/055BEFBC92E6ACA1E996A2E695B0EFBC8FEFBC92E6ACA1E996A2E695B05DE5B9B3E696B9E6A0B9E291A1.gif)
この関数は指数関数 exp(x) を3段構えで抑え込んでいます:
①変数 x を pi で割る。
②平方根をとる。
③2次関数の平方根で割る。
これだけ抑え込むと、さすがの指数関数もその効果をなかなか現しません。分母の減衰効果が先に効いて振幅をいったん小さくし、そのあと x = 8 以降に緩やかに振幅を回復させていきます。
⇒ なんとなくの数学日記(るきさん)