放物螺旋
アルキメデス螺旋 (r = θ) は周回ごとの曲線は等間隔で描かれていましたが、θの平方根をとることによって間隔を変化させることができます:r = a √θ
a はグラフ全体の拡大・縮小に関係するだけのパラメータなので、今は a = 1 と定めておきます。すると (x, y) とθの関係は次のように表せます。
x = √θ cosθ, y = √θ sinθ
√θ はθ が増すほどその増加率は減少していくので、
双曲螺旋のグラフを描いてみると・・・・・・

このように周回ごとの曲線間隔が狭くなっていくのです。
間隔を変化させる螺旋は他にもたくさんあります。
その中でも簡単な例は対数関数を組み込んだ極方程式です:
r = log θ (注:底は e です)
しかし放物螺旋とは異なる振る舞いをします:

このグラフは漸近線をもちます (y = 0)。すなわち -∞ から原点までほぼ直線状に伸びて来て、そこから渦を巻き出します。曲線間隔は対数関数に従って徐々に狭まっていきます。
双曲螺旋
極方程式でθの逆数をとれば、やはり間隔を変化させる螺旋が描くことが予想できます。それが 双曲螺旋 の方程式です。r = a/θ
a = 1 とすると (x, y) と θ の関係は
x = cosθ/θ, y = sinθ/θ
となります。この方程式はとても美しいグラフを描きます:

漸近線は y = 1 。無限遠方から大きな弧を描きながら周回しつつ徐々に間隔を狭めていき、最終的に近づいていきます。しかし原点付近では曲線の密度がどんどん増し、なかなかその半径を小さくしません。θ → ∞ でようやく原点に達することができます。
双曲螺旋を少し変形して、
x = cosθ + cosθ/θ, y = sinθ + sinθ/θ
という関数を定めてグラフを描いてみます:

θ → ∞ で
x = cosθ, y = sinθ
となりますから、半径 1 の円に巻きつく螺旋になっているわけです。円の付近では線が密になりすぎて見えにくいので、本当に螺旋を描いているのかどうか、x = 1 の付近を拡大してみます。
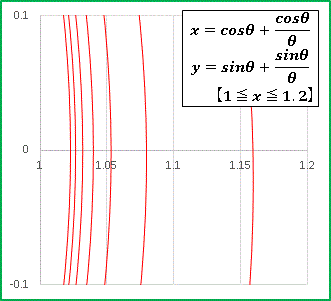
きちんと線が分かれていることが確認できますね。エクセルグラフでは目盛を自由自在に変えられるので、こういうことも簡単にできてしまいます。