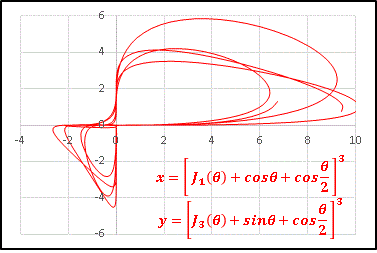
�g�����̊T�O���������E�ɍL���܂�
�@n �̂��̂��� k �Ƃ�g�����̐���
�@
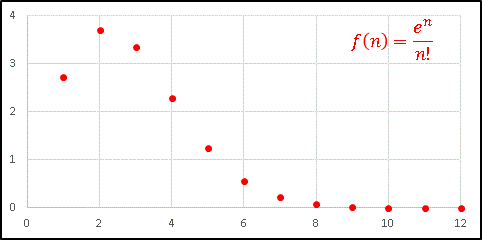
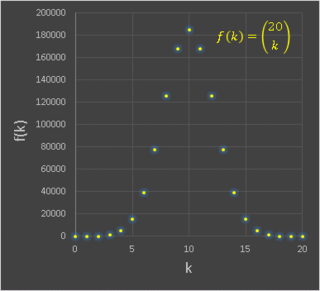
�ŕ\����܂��B���Ƃ��� n = 20 �̏ꍇ�ɁAk �̊��Ƃ���
20C
k ���v���b�g����Ǝ��̂悤�ɁA���E�Ώ̂̃O���t���`����܂��B
�@
�@�g�����̎��ɂ����Ă� n �� k �������Ȃ̂ŁA
nC
k �������l�����Ƃ�܂��A�����ŊK��������͈͂܂Ŋg�������K���}��
�@
���g���ƁA�g�����̐������߂鎮�������͈͂܂Ŋg�����邱�Ƃ��ł��܂��B���Ȃ킿�As �̂��̂��� x �I�Ԑ� (s, x �͂Ƃ��Ɏ���)��g������
�@
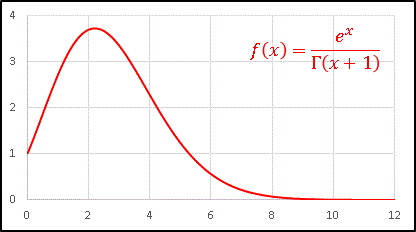
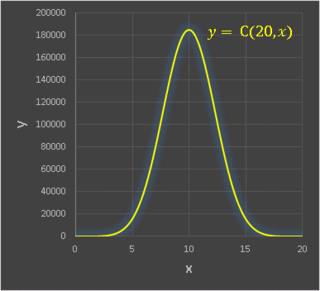
�ɂ���Ē�`����u 8.5 �̂��̂���A2.3 ���Ƃ�g�����̐��v�Ƃ�����Ȃ��̂��v�Z�ł���킯�ł��i���͂⌻�����E�̎��ۂƂ͑Ή����Ă��܂���j�B�ϐ��������Ɋg�����ꂽ�̂ŃO���t�����炩�ɂȂ���܂��B�����قǂ�
20C
k �ɑΉ����� C(20, x) �̃O���t��`���Ă݂�Ǝ��̂悤�ɂȂ�܂��B
�@
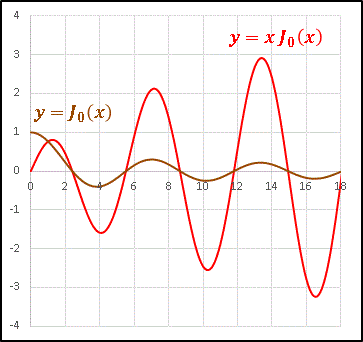
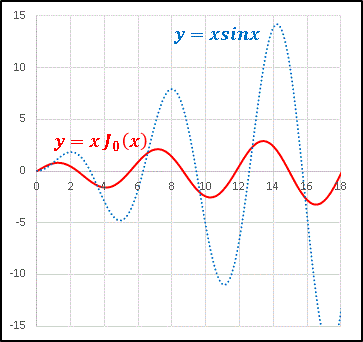
�@���̂悤�ɁA�ŏ��͌������E�ɑΉ������Đ��܂ꂽ�T�O���A�������w�̐��E�Ɏ������܂��ƁA�����玟�ւƊg����`���邱�Ƃ��ł��܂��B���ہA�K��̊g���T�O�ł���K���}���͎����ǂ��납���f�ϐ��Œ�`����Ă���̂ŁA��낤�Ǝv���Αg�����̎������f�����E�܂ōL���邱�Ƃ��ł���̂ł��B
�@


 �@
�@