アステロイドに収束する曲線
今回はアステロイドの方程式にベッセル関数 Jn を組み込んでみます。ベッセル関数は減衰振動関数です。詳しい解説はこちらを参照してください。
まず最初に
x = [J0(θ) + cosθ]3
y = [J0(θ) + sinθ]3
y = [J0(θ) + sinθ]3
という方程式の様子を見ます:

-4π ≦ θ ≦ 4πの範囲で描いています。ベッセル関数は原点付近にピークを持ち、|θ| の増加にともなって減衰していく関数なので、 θ ≪ 0 (θ がとても小さいところ)では動点 (x, y) は図の内側に描かれたアステロイドに近い軌道を描きます。θ が 0 に近づくとベッセル関数の影響が大きく現れるので外側の大きな軌道へ移ることになります。そのあとまたθの増加とともに内側 へ入り込んでいき、θ ≫ 0 (θがとても大きいところ)ではまたアステロイド付近をぐるぐる回ることになります。
基本はこの形ですが、 Jn の number を変えていくとより複雑な軌道を描くようになります。まとめて掲載しておきます。

いずれも |θ| ≫ 0 ではアステロイドに収束する曲線です。
最後におまけとして
x = [J1(θ) + cosθ + cos(θ/2)]3
y = [J0(θ) + sinθ + cos(θ/2)]3
y = [J0(θ) + sinθ + cos(θ/2)]3
という方程式のグラフを描いてみます:
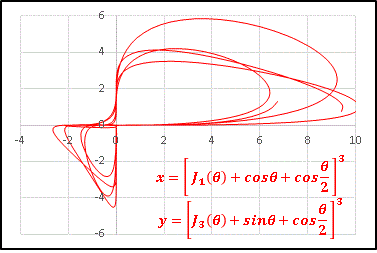
もはやアステロイドとは関係ありませんが、媒介変数表示関数の描く模様はいまだに全く予測できませんね。
≫ [Amazon数学書籍] ピーター・フランクルの超数脳トレーニング
ベッセル関数はどこから?
ベッセル関数(Bessel function)はドイツの天文学者ベッセル( Friedrich Wilhelm Bessel)さんが考案した関数なので、こう呼ばれています。ベッセルさんは三体問題の研究によって摂動理論を作ったり、海王星の存在を予測したり、地球の子午線測定を指揮して精密な扁率を決定したり(地球科学を勉強している人にはベッセル楕円体はお馴染みですね)と多方面で活躍した人です。さてベッセルさんは「惑星の楕円軌道の距離 r を角度 θ = ωt の関数としてうまく表現する方法はないものか」と思案を重ねて、 r をフーリエ級数展開する方法を思いつきました。その係数の中にベッセル関数が現れたのです。ベッセルさんは「よしよし、これで何でも計算できるわい」と単に天文の計算目的に使うにとどまらず「うーむ。何だか面白そうな関数が現れたぞ。数学的にどのような性質を持つのだろう?」と一般的な整数次ベッセル関数の研究をまとめました。
かくして現代では Excel などのソフトにも欠かせない関数の1つとして標準装備されるようになり、主に物理や工学分野で活発に利用されています。