Excel VBA　数学実験室

小さな結び目が現れます

　前回のスーパー楕円変形版に三角関数を組み込んで


という方程式を作ってみました。

　

　両端に小さな結び目が現れましたね。
　すでに楕円とはいえませんが、楕円らしき面影を残してはいます。
　cos^q x の代わりに sin^q x を組込んで


としてみると ......

　

　蝶ネクタイみたいな形になります。
　他にも色々バリエーションがありますけど、
　特に面白かったのは cos^q x sin^q x を組込んだ


という方程式です。

　

　蝶ネクタイの両端にさらに小さな結び目があるという、何だか愛嬌のある曲線です。
　 　

≫ [Amazon書籍] 詳解ディープラーニング（TensorFlow・Keras）

角の切り取りが非対称になります

　前回扱ったスーパー楕円の方程式を再掲します。


　今回はこの式を少し変形して


という新しい楕円方程式を考察してみます。 (a, b) = (1, 2) と固定し、


としてパラメータ (p, q) を動かしてみます。まずは (p, q) = (2, 3) とすると ......

　

　こんな形になります。 (p, q) = (3, 2) としてみると ......

　

　p と q を入れ替えただけで、かなり様相が違っていますね。
　スーパー楕円と異なるのは、角の切り取り方にバリエーションが生じるということです。分かりやすいように (a, b) = (1, 1) として方程式を


と書き直して調べてみます。ただし −1 ≦ x ≦ 1 , −1 ≦ y ≦ 1 という範囲に制限しておきます。楕円というよりは円の変形版ですが、とりあえず p = q = 3 としてグラフを描いてみましょう。

　

　このように p = q ならば y = x について対称な形のグラフになっています。
　これを (p, q) = (2, 4) のように変えてみると ......

　

　今度は y = x について非対称となります。
　つまり角の切り取り方が非対称になっているということです。
　さらに a や b もパラメータとして色々変えてみると、様々な楕円ができますので、皆さんもエクセルで試してみてください。
　 　

≫ [Amazon書籍] パソコンで楽しむ　自分で動かす人工知能

スーパー楕円（建築、インテリア、テーブル、ホットプレート ... ）

　「四角いようなー、丸いような−」みたいな物って意外と身近にありますよね。
　ほら、テーブルとかホットプレートのように長方形から角をとった形です。
　この形状は数学者でもあり詩人、そして建築家でもあるピート・ハイン (PietHein) というデンマーク人によって考案されました。その名も スーパー楕円 です！　
　スーパー楕円は当初ストックホルムの都市計画に採用され、今では建築やインテリアデザインなど様々な分野で目にする形となりました。でもスーパー楕円は正式な数学用語ではないという話もあって、そのへんのところは私もまだよく理解していません。おそらくもっと広範に包括する代数曲線があると思うのですが、とりあえず世間一般（？）に知られるスーパー楕円は


という式で定義され、もちろん普通の楕円 (p = 2) も含みます。
　一般的には p ＞ 2 をスーパー楕円とよびます。 a = 2, b = 1 を固定すると


となります。この式で p を変化させてグラフを描いてみます。

　

　緑、青、赤の順に p = 2, 3, 4 としてあります。
　緑色の楕円から徐々に長方形に近づいている様子がわかりますね。
　スーパー楕円は p → ∞ の長方形も含む方程式です。
　ちなみに一般的によく使われている形状が p = 2.5 としたものです。

　

　この形状に限ってスーパー楕円と呼ぶ人もいるようです。
　今度は逆に p = 1 から値を小さくしていきましょう。

　

　ひし形（ p = 1 ）から星形へ縮んでいく様子がわかります。
　この形は本質的にアステロイドと同じもので、実は以前にも


という方程式で似たような形を扱っています。 p → 0 とすると十字の線分へと収束していきます。次回はこのスーパー楕円方程式を少し変形してみる予定です。
　 　

≫ [Amazon書籍] ゲーデル、エッシャー、バッハ（あるいは不思議の環）

�@ 鋭くカーブする直線

　次のような２次方程式を考えます。


　x が実数解をもつ範囲を考えます。判別式を D とすると


なので実数解をとる範囲は a ≦ −1, および 1 ≦ a です。解は


と表されます。ここまでは数学�TA の演習問題などでおなじみですね。しかし本当に知りたいのは x が a を変数としてどのような曲線を描くかということです。さっそく Excel で図示してみると ......

　

　鋭くカーブした曲線が２つ現れました。
　最初に確認したように区間 (−1, 1) には解は存在していません。
　a = ±1 以外では実数解は２つ存在するので、１つの a に対して 2 つの x が対応します。|x| を大きくしていくと片方の解は 0 へ収束していきますが、もう一方の解は ±∞ となります。

�A 星形のようなグラフ

　係数が変われば曲線 x = f(a) の形も変化します。


という方程式の解を調べてみましょう。解の公式から


が得られます。この式から a = 1 では解をもたないことがわかります。 x が実数解である範囲は 0 ≦ a ＜ 1, 1 ＜ a ≦ 2 です。 x = f(a) のグラフは次のようになります。

　

　星形のようなグラフですね。a が 0 あるいは 2 に近いところでは２つの解が非常に近い値をとることがわかります。 a → 1 で解は ±∞ となります。
　 　

≫ [Amazon書籍] 数学の言葉で世界を見たら（父から娘に贈る数学）

3 次関数の 1 次の項と 2 次の項の係数の関係

　今回は x の 1 次と 2 次の項が含まれる


という 3 次関数について調べてみます。この場合、 1 次の項の係数と 2 次の項の係数の関係 によって様子が変わります。y を微分すると


となるので、y' = 0 となる点は


という 2 次方程式で求められるのですが、この方程式が実数解をもつかもたないかで、グラフの様子が変わってしまいます。判別式は


ですから、とりあえず c ≦ 1 / 3 であれば実数解をもつので、まずその場合を考えてみます。 [2] から c = − 3 x² − 2 x を [1] に入れると簡単に極値の軌跡が求められます：


　c = 0, −2, −4 と変化させたグラフを描いてみると ......

　

　軌跡に沿って、極大値は左上に極小値は右下に移動しています。このように、 c ≦ 1 / 3 のときは c が小さくなるほど極大値の山を高くし、極小値の谷を深くしていく効果があることがわかります。

　次は [2] が虚数解をもつ場合 (c ≧ 1 / 3) を考えます。つまり極値をもたない場合です。 c = 1, 2, 3 でグラフを描いてみると ......

　

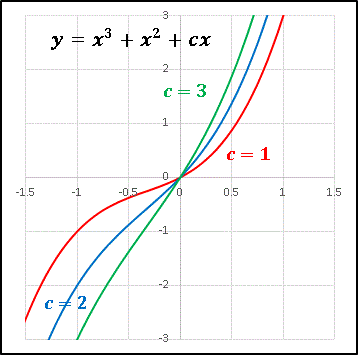
　c の増加と共にカーブがなくなってゆく様子がわかります。

　こうした違いは x³ に対して x の項がどちら側に寄与するかに起因しています。簡単のために c が負であるときを考えると、増加しよう（あるいは減少しよう）という x³ の傾向に対して、1 次の項が反対符号に作用させる効果となり、山や谷を形成します。ただ x² の項は常に正方向に効くので、|極大値| ＞ |極小値| という関係になっています。また c ＞ 0 であれば x³ と同じ正方向に寄与します。 c ≧ 1 / 3 のときは極値をつくりません。ただ、 c ＜ 1 / 3 であるときは x が負の領域で x² の寄与が勝って小さな極大値をつくります。また同じく負の領域で目に見えないぐらいの極小値も存在します。非常に細かい話になりますが、|x| ≪ 1 では x³ が c x に勝って負の値をとるからです。下図に c = 0.1 のグラフの拡大図を載せておくので、参考にしてください。

　

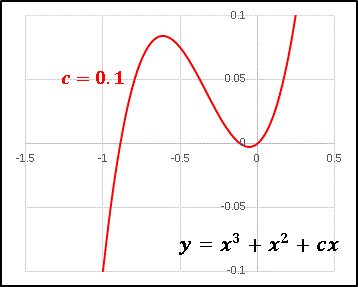
　このように、3 次関数における極値の様子はパラメータ同士の微妙な兼ね合いによって変わってしまうのです。