① 鋭くカーブする直線
次のような2次方程式を考えます。
x が実数解をもつ範囲を考えます。判別式を D とすると
なので実数解をとる範囲は a ≦ -1, および 1 ≦ a です。解は
と表されます。ここまでは数学ⅠA の演習問題などでおなじみですね。しかし本当に知りたいのは x が a を変数としてどのような曲線を描くかということです。さっそく Excel で図示してみると ......
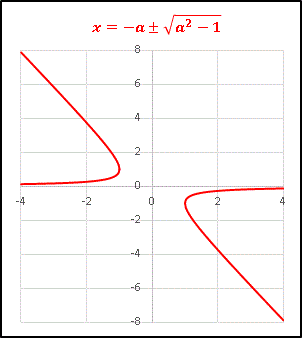
鋭くカーブした曲線が2つ現れました。
最初に確認したように区間 (-1, 1) には解は存在していません。
a = ±1 以外では実数解は2つ存在するので、1つの a に対して 2 つの x が対応します。|x| を大きくしていくと片方の解は 0 へ収束していきますが、もう一方の解は ±∞ となります。
② 星形のようなグラフ
係数が変われば曲線 x = f(a) の形も変化します。
という方程式の解を調べてみましょう。解の公式から
が得られます。この式から a = 1 では解をもたないことがわかります。 x が実数解である範囲は 0 ≦ a < 1, 1 < a ≦ 2 です。 x = f(a) のグラフは次のようになります。
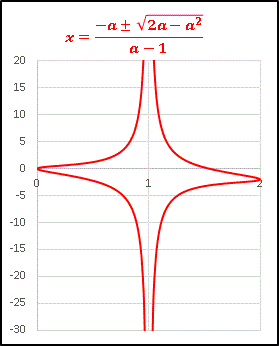
星形のようなグラフですね。a が 0 あるいは 2 に近いところでは2つの解が非常に近い値をとることがわかります。 a → 1 で解は ±∞ となります。