Excel VBA　数学実験室

≫ [Amazon数学書籍] 一般相対性理論（ディラックの記号法で宇宙の方程式を解く）

増幅因子をかけて減衰を打ち消して振幅を増加させます

　減衰周期関数であるベッセル関数 J_n(x) に x という 増幅因子 をかけたらどうなるかという実験です。まず J₀(x) と x J₀(x) のグラフを並べて比較してみます。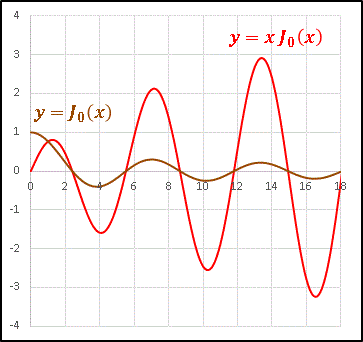

　

　x という因子が J₀(x) の減衰を打ち消して、y = x J₀(x) は振幅を増加させる関数となっています。次は普段からよく目にする振幅増加関数である y = x sinx と比較してみます。

　

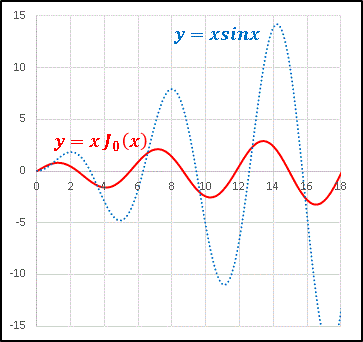
　青い点線が y = x sinx のグラフです。
　x sinx と比較すると x J₀(x) の振幅増加はとても緩やかですね。
　最後に y = J_n(x) について n = 1, 2, 3 のグラフを並べてみます。

　

　J_n(x) は n が大きくなるほど立ち上がりが遅くなる関数ですから、x をかけてもその特徴は維持されます。
　
≫ [Amazon数学書籍] 保型関数（古典理論と現代的応用）

オリンピックが始まりました

　リオ五輪が始まりましたね！　男子サッカーの初戦は残念な結果に終わってしまいましたが、まだまだ始まったばかりです！　本日も開会式、女子バレーボール、柔道など見どころ満載です。私も時間のある限り日本選手を応援しますよ ...... といいつつ、朝の開会式を観ることができませんでした（この記事を書いてました）。でも夜の録画放送で観る予定です。
　それにしてもブラジルは日本の反対側ですから時差が大きいのが難点です。柔道の決勝は夜中になるんですよね。柔道の試合だけは（メダルの可能性も大きいので）何としても見たいんですが ...... なるべく頑張って起きていようと思います。