アルキメデスの螺旋(渦巻線)
ロープをぐるぐると巻けばアルキメデスの螺旋が出来上がります。古代シラクサの数学者アルキメデスさんも船着き場で巻かれたロープをじっと観察していたのかもしれません。別にそんなことしなかったかもしれません。まあともかく極方程式の中でもっとも簡単な式で表せるグラフが アルキメデスの螺旋(Archimedes' spiral)です:r = aθ
a = 1 と決めてしまえば、
r = θ
となって、さらに簡素な方程式になります。偏角θが増せば動径 r も大きくなるのですから、数学に慣れた人はこの方程式を見ただけで螺旋を描くことがわかります。x, y を具体的に表示すると、
x = θcosθ (1)
y = θsinθ (2)
y = θsinθ (2)
となります。さっそくいつものようにグラフを描いてみましょう。
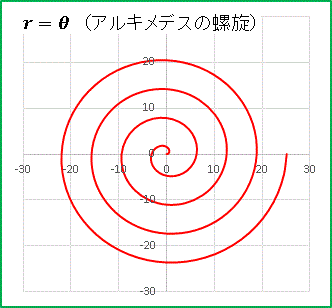
紛れもなく螺旋ですね。ここで (1) と (2) をθで微分してみますと
dx = (cosθ - θsinθ)dθ (3)
dy = (sinθ + θcosθ)dθ (4)
dy = (sinθ + θcosθ)dθ (4)
となります。この dx と dy の意味を考えます。

上図はアルキメデスの螺旋を拡大表示したものです。 dx と dy は微小角 dθ に対する線分の増加 ds の x 成分、y 成分となっていますね。図にあるように螺旋が1周するごとに ds は大きくなっていますから、dx と dy の絶対値も大きくなっていきます。その効果は (3) と (4) の第2項 sinθ, cosθ の前にかかるθで表されています。ここから予想されることは、あらためて
x = cosθ - θsinθ (5)
y = sinθ + θcosθ (6)
y = sinθ + θcosθ (6)
とおいてみたときに、この方程式もまた螺旋を表しているのではないかということです。それではエクセルを使って実際に試してみましょう:
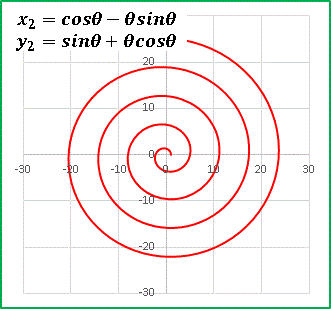
予想通りですね。向きは逆になっていますが、やはり渦を巻いています。とすると (5), (6) を再び θ について微分しても ......
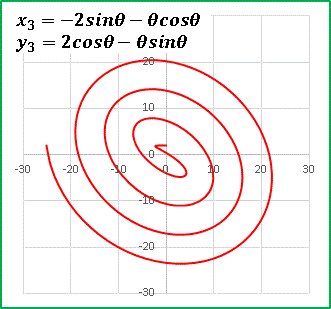
やはり螺旋が出来上がります。何度繰返し微分しても新しい形の螺旋が生まれてきます。ちなみにベクトル (dx/dθ, dy/dθ) を (1 + θ2) の平方根で割って規格化すると、任意の θ における接線ベクトルが得られます:

ちなみにアルキメデスさんも任意の点における接線を求めることに成功していたようです。彼が生きた時代は紀元前ですから、当然デカルト座標も解析幾何学も用いることはできませんでした(つまり上のように機械的に計算できるような問題ではなかったということです)。当時の幾何学の知識だけで問題を解決したわけですから、本当にすごい人ですね。