�A���L���f�X�̗����i�Q�����j
�@���[�v�����邮��Ɗ����A���L���f�X�̗������o���オ��܂��B�Ñ�V���N�T�̐��w�҃A���L���f�X������D������Ŋ����ꂽ���[�v�������Ɗώ@���Ă����̂�������܂���B�ʂɂ���Ȃ��Ƃ��Ȃ�������������܂���B�܂��Ƃ������ɕ������̒��ł����Ƃ��ȒP�Ȏ��ŕ\����O���t�� �A���L���f�X�̗����iArchimedes' spiral�j�ł��Fr = a��
�@a = 1 �ƌ��߂Ă��܂��A
r = ��
�ƂȂ��āA����Ɋȑf�ȕ������ɂȂ�܂��B�Ίp�Ƃ������Γ��a r ���傫���Ȃ�̂ł�����A���w�Ɋ��ꂽ�l�͂��̕����������������ŗ�����`�����Ƃ��킩��܂��Bx, y ����̓I�ɕ\������ƁA
x = ��cos�Ɓ@�@�@(1)
y = ��sin�Ɓ@�@�@(2)
y = ��sin�Ɓ@�@�@(2)
�ƂȂ�܂��B�������������̂悤�ɃO���t��`���Ă݂܂��傤�B
�@
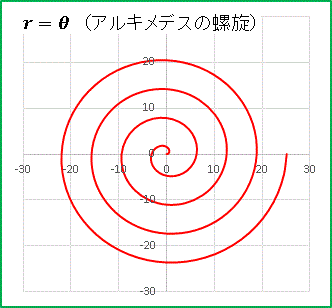
������Ȃ������ł��ˁB������ (1) �� (2) ���ƂŔ������Ă݂܂���
dx = (cos�� - ��sin��)d�Ɓ@�@�@(3)
dy = (sin�� + ��cos��)d�Ɓ@�@�@(4)
dy = (sin�� + ��cos��)d�Ɓ@�@�@(4)
�ƂȂ�܂��B���� dx �� dy �̈Ӗ����l���܂��B
�@

�@��}�̓A���L���f�X�̗������g��\���������̂ł��B dx �� dy �͔����p d�� �ɑ�������̑��� ds �� x �����Ay �����ƂȂ��Ă��܂��ˁB�}�ɂ���悤�ɗ������P�����邲�Ƃ� ds �͑傫���Ȃ��Ă��܂�����Adx �� dy �̐�Βl���傫���Ȃ��Ă����܂��B���̌��ʂ� (3) �� (4) �̑�Q�� sin��, cos�� �̑O�ɂ�����Ƃŕ\����Ă��܂��B��������\�z����邱�Ƃ́A���炽�߂�
x = cos�� - ��sin�Ɓ@�@�@(5)
y = sin�� + ��cos�Ɓ@�@�@(6)
y = sin�� + ��cos�Ɓ@�@�@(6)
�Ƃ����Ă݂��Ƃ��ɁA���̕��������܂�������\���Ă���̂ł͂Ȃ����Ƃ������Ƃł��B����ł̓G�N�Z�����g���Ď��ۂɎ����Ă݂܂��傤�F
�@
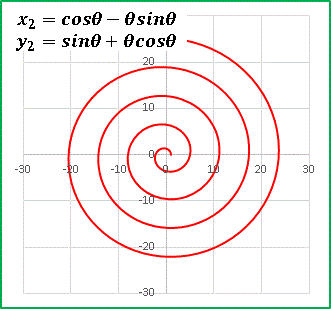
�@�\�z�ʂ�ł��ˁB�����͋t�ɂȂ��Ă��܂����A��͂�Q�������Ă��܂��B�Ƃ���� (5), (6) ���Ă� �� �ɂ��Ĕ������Ă� ......
�@
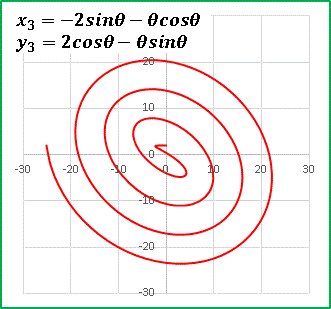
�@��͂藆�����o���オ��܂��B���x�J�Ԃ��������Ă��V�����`�̗��������܂�Ă��܂��B���Ȃ݂Ƀx�N�g�� (dx/d��, dy/d��) �� (1 + ��2) �̕������Ŋ����ċK�i������ƁA�C�ӂ� �� �ɂ�����ڐ��x�N�g���������܂��F
�@

�@���Ȃ݂ɃA���L���f�X������C�ӂ̓_�ɂ�����ڐ������߂邱�Ƃɐ������Ă����悤�ł��B�ނ�����������͋I���O�ł�����A���R�f�J���g���W����͊w���p���邱�Ƃ͂ł��܂���ł����i�܂��̂悤�ɋ@�B�I�Ɍv�Z�ł���悤�Ȗ��ł͂Ȃ������Ƃ������Ƃł��j�B�����̊w�̒m�������Ŗ������������킯�ł�����A�{���ɂ������l�ł��ˁB
�@ �@