���[�Ō��������
�@�O��Ɉ��������Ė������ł��B�@�܂��͔�r�I�V���v���Ȃ��̂���F
�@
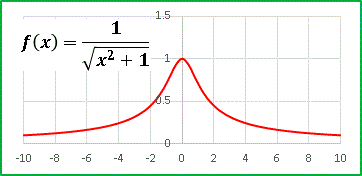
�@f(0) = 1 �_�Ƃ��鍶�E�Ώ̂̎R�Ȃ�̊��ł��B
�@y = 1/x �ɋ߂����z�����Ȑ��ł����A����͕K�����l���Ƃ�̂� x = 0 �Œ�`������炩�ɘA������Ă��܂��B���̊��ɎO�p�����|���Ă݂܂��傤�B
�@
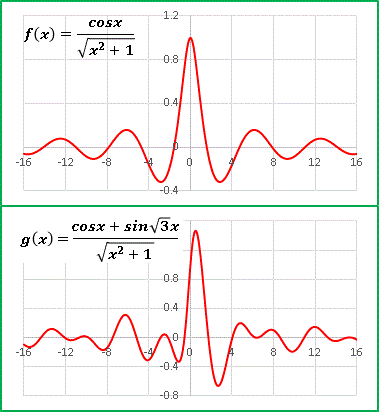
�@f(x) �͌��_�Ƀs�[�N�������A���[�Ō������Ă������B
�@g(x) �͊T�������ł���������͕���Ă��܂��Ă��܂��B
�@������ x �� �}�� �� 0 �Ɏ������邱�Ƃɂ͕ς�肠��܂���B
�����I�Ɋ��炩�łȂ��_������܂�
�@���� 1 + sin[pi*x]�ƁA���̕��������Ƃ������ł��F�@
![03[1+sin��x]������.gif](/excelmathfunction/file/035B12BsinCF80x5DE5B9B3E696B9E6A0B9.gif)
�@f(x) �͑S��Ŋ��炩�Ȋ��ł����Ag(x) �� x = 1.5, 3.5, 5.5, �c�c �Ƃ������炩�ł͂Ȃ��_�������I�Ɍ���܂��B���炩�ł͂Ȃ��Ƃ����̂͂܂�A���̓_�Ŕ�������`�ł��Ȃ��Ƃ������Ƃł��Bg(x) ��������Ă݂��
�ƂȂ�܂��ˁBg(x) �����̂܂ܕ���ɓ����Ă��܂�����A x = 1.5, 3.5, 5.5, �c�c �ł��̊����`���邱�Ƃ͂ł��܂���B
y = 1 �Ɠ����ȃO���t�H
�@���͕���E���q�����ɂQ�����̕������Ƃ�����F�@
![04[�Q�����^�Q����]�������@.gif](/excelmathfunction/file/045BEFBC92E6ACA1E996A2E695B0EFBC8FEFBC92E6ACA1E996A2E695B05DE5B9B3E696B9E6A0B9E291A0.gif)
�@x ���傫���̈�ł� f(x) �� 1 �Ƃ݂Ȃ����Ƃ��ł��܂��B�܂蒼�� y = 1 �Ƃقړ����ȃO���t�ƍl���邱�Ƃ��ł��܂��B���\�Ȃ悤�ł��� x �� �}�� �ł͌����ɂ��ꂪ���藧���܂��B
�@f(x) �� cos[pi*x] ���|�������� g(x)�ł��B���_�t�߂ŏ����r�����������܂����Ax ���傫���̈�ł͕��ʂ̎O�p���Ƃ��ĐU�镑���܂��B
�@g(x) �ɂ����ĕ��q���S�����̕������Ƃ����̂� h(x) �ł��B�U���͌��_����Q�����I�ɑ������Ă������ƂɂȂ�܂��B
�@�Ō�� g(x) �̕��q���w�����̕������Œu�������Ă݂܂��F
�@
![05[�Q�����^�Q����]�������A.gif](/excelmathfunction/file/055BEFBC92E6ACA1E996A2E695B0EFBC8FEFBC92E6ACA1E996A2E695B05DE5B9B3E696B9E6A0B9E291A1.gif)
�@���̊��͎w���� exp(x) ���R�i�\���ŗ}������ł��܂��F
�@�@�ϐ� x �� pi �Ŋ���B
�@�A���������Ƃ�B
�@�B�Q�����̕������Ŋ���B
�@���ꂾ���}�����ނƁA�������̎w���������̌��ʂ��Ȃ��Ȃ������܂���B����̌������ʂ���Ɍ����ĐU�����������������A���̂��� x = 8 �ȍ~�Ɋɂ₩�ɐU���������Ă����܂��B
�@
�邫����
�@�m��l���m��A�m��Ȃ��l�͂܂������m��Ȃ�����w�邫����x��ǂݒ������肵�Ă��܂��B�邫����Ƃ��������Ƃ����Q�l�g�̏����̓����`��������ł��B�����Ƃ�̂�т肵�����i���Ǝv���Ă����邫���A���������т�����Ȑ��i�ŋ����Ă��܂��B�}���ق̎q�������̖{���u���ꂽ�R�[�i�[�ɓ��X�Ɛw����āA���ɂ����q���Ɩ{����荇����ʂȂ�āA�܂�Ŏq�����̂��́i�邫����̎��N��͂����炭 30 �ΑO�ゾ�Ǝv���܂��j�B�@�������ӂƎv���Ɓw�邫����x�͎��̏���������u���O�ɂ��Ȃ�e����^���Ă���悤�ȋC�����܂��B�w�p��̊فx��w����q����̃u���O�x�œW�J���Ă���w���Ƃ����V���[�Y�x�̏��t�����ƍ����́A�u�邫����Ƃ��������̊W�ɂ悭���Ă���Ȃ��v�ƍ�����Ȃ���Ɏv�����肵�Ă��܂��B���t���������Z���Ƃ͎v���Ȃ��قlj�ԂŎq�����ۂ����i�ł�����ˁB
�@�����ď��t�����A�����������ƂR�O��A�S�O��ɂȂ��Ă������ƒ��ǂ��ꏏ�ɏ��F�B���Ă���̂ł��傤�B�������w���Ƃ����V���[�Y�x�̓��A���^�C���`���Ői�s���Ă��܂�����A���������p��`���͖̂{���� 10 �N�ȏ��Ƃ������ƂɂȂ�܂��ˁc�c����܂Ńu���O�������Ă���̂��A���������Ď����ł��킩��܂���B���������Ƃ͎v���Ă��܂����ǂˁB�ł��Ƃ肠�����A���N�̂S���ɂ͏��t������͍��Z�R�N���ɂȂ�܂��B���ł��ˁB���t�����͂Ƃ������A�����͎u�]�Z�̍��i��ڎw���Ĉꐶ����������ł��傤�B�ł������ƁA���������Ƃ��� "���Ƃ����" ���ӂ�ӂ���ŗ��Ďז������ł��傤���ǂˁB
�@ �@