�g���N�g���b�N�X�i�ǐՐ��^�������j
�@�������Ƃ����Ȑ��ƌĂꂽ������܂��B
�@�u���H�@���Ȑ��H�v�Ƌ�����邩������܂��A���}�����Ă��������������B
�@
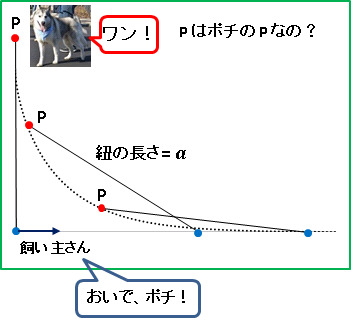
�@�|�`�iP�j�͎����傳��ɐL�яk�݂��Ȃ��R�łȂ���Ă��܂��B
�@�ŁA�}�ɂ���悤�Ɏ����傳��͐����ړ����Ă����̂ł��B
�@�|�`�͊��������ɐK����U���Ď����傳��̌��ǂ��킯�ł����A���̂Ƃ��|�`�̓����O�Ղ��g���N�g���b�N�X�ł��B�ł��u���Ȑ��v�Ȃ�Ă���܂�ł���ˁB�Ȃ̂ŁA�����Ǝ����傳��̈���`��肻���Ȗ��O�����Ă����܂����B���Â��āc�c
��̂��U���Ȑ�
�ł��I�@�ǂ��ł����H�@�_���H�@����Ȃ�c�c
�|�`�Ɗy�������U���Ȑ�
������_���ł����H�@�܂��F����̂��D���Ȗ��O�ŌĂ�ł��������ȁB
�g���N�g���b�N�X�͎��̂悤�Ȕ����������̉��ɂȂ��Ă��܂��F
(a 2 - y 2) y��2 = y 2
�@�v�킸�u���I�v�ƚX�肽���Ȃ�悤�ȋ��ʂ̎��ł����A�������ʂ肯�������苭���������ł��B�����������̈����Ɏ��M�̂�����͉����Ă݂Ă��������B�u�ǂ����Ă���������m�肽���I�v�Ƃ����R�����g������Ή�@���ڂ��܂����A�ł�����̃R�����g�͊��ق��Ăق����ł��i��������̐������u���O�ɍڂ���͖̂{���Ɏ�Ԃ�������̂ł��j�B�l�b�g����w�̐}���قŒT�����Ԃ���܂��B
�@���͑ΐ����܂A���iimplicit function�j�ŕ\����܂��F
�@�萔���ς킵���̂� a = 1 �Ƃ��Ă����܂��傤�F
�@�}��ϐ� t ��p����ƁA
x = t - tanh(t),�@y = sech(t)�@�@�@[2]
�̂悤�ɊȒP�Ȍ`�ɏ����܂����A����� [1] �̂܂܂Řb��i�߂܂��B
�@
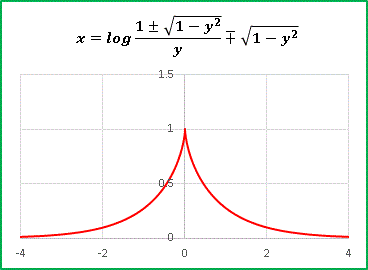
�@x = 0 �Ő낪�����`�̃O���t�ł��B
�@���̐낪��� ��c �̍��Ɍ���������܂��B
�@������m���߂邽�߂ɁA���̍�����������Ă݂܂��傤�F
�@
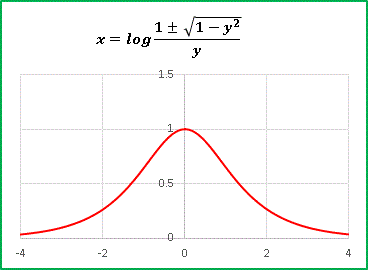
�@�낪�肪�Ȃ��Ȃ��Ċ��炩�ɘA�����Ă��܂��ˁB
�@�ł͍Ăэ������ɖ߂��āAlog(�c) �̍��� cos(y) �������Ă݂܂��F
�@
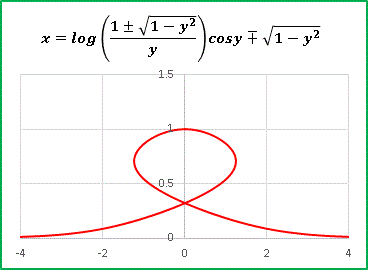
�@���_�t�߂ł����ƂP��������ł��B
�@cos(y) �̑���� exp(y) ��������ƁE�E�E�E�E�E
�@
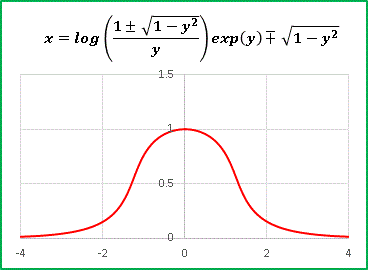
�@�ۂ݂�тт��X�q�̂悤�Ȍ`�ɂȂ�܂����B
�@�Ō�ɗ~������ cos(y) �� exp(y) �̗����������Ă݂�ƁE�E�E�E�E�E
�@
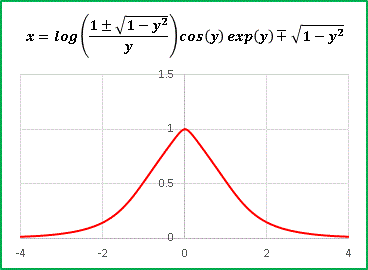
�@�O�p�X�q�̏o���オ��B����͂���ł����܂��B
�@�� �Ȃ�ƂȂ��̐��w���L�i�����݂��\�������������܂����j �@