r = θ
というもっとも基本的な螺旋です。(x, y) は
x = θ cosθ, y = θ sinθ
と表せました。
方形らせん(方形が拡大されていきます)
今回はアルキメデス螺旋を少し変形して
x = θ cos2θ, y = θ sin2θ [1]
という関数を考えてみます。さっそくグラフを確認してみましょう:
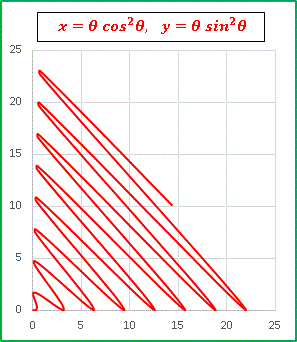
奇妙なグラフが現れましたね。このグラフを見ると [1] から媒介変数 θ を消去することはできそうにありません(x と y だけでこのような複雑なグラフを表現することは不可能だと思います)。しかし [1] から x と y は
x + y = θ
という関係にあることだけはわかります。
つまり θ を 0 から動かし始めた場合、
x + y = 0
x + y = 0.1
x + y = 0.2
x + y = 0.3
・・・・・・
x + y = 1.0
x + y = 1.2
・・・・・・
x + y = 0.1
x + y = 0.2
x + y = 0.3
・・・・・・
x + y = 1.0
x + y = 1.2
・・・・・・
というように、(x, y) は少しずつ切片の変化する直線上を動き続けるわけです。結果として x 軸と y 軸で折り返す波のようなグラフができあがりますが、実はこの曲線は螺旋を第1象限の中に閉じ込めた形なのです。これを普通の螺旋に表示し直すには前回定義した、
x = cosθ |cosθ| p - 1
y = sinθ |sinθ| p - 1
y = sinθ |sinθ| p - 1
という形を基礎にした方程式が必要となります。
今回は p = 2 として x, y にそれぞれ θ をかけた方程式:
x = θ cosθ |cosθ|
y = θ sinθ |sinθ|
によって実数全域に拡大できます:y = θ sinθ |sinθ|
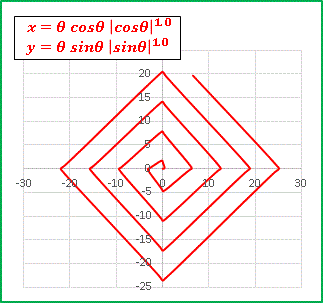
方形を拡大していくような螺旋が現れましたね!
「方形螺旋」と名づけておきましょう。
アステロイドに対しても同じような変形を加えてみます。
アステロイドの方程式は
x = cos3θ, y = sin3θ
ですね。三角関数の指数が奇数の場合は絶対値記号を使わなくても、そのまま螺旋形へ拡大できます:
x = θ cos3θ, y = θ sin3θ
としてグラフを描いてみますと……
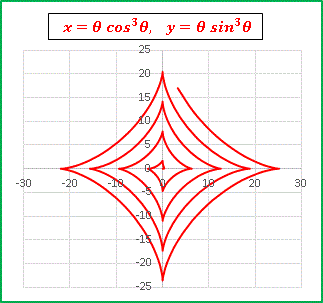
はい。アステロイド螺旋のできあがり!
それにしても数学のグラフって、少し手を加えるだけで無数のバリエーションが生じるので本当に面白いですよね。それではまた次回お会いしましょう!
⇒ なんとなくの数学日記(私の好きな漫画ベスト3)