都立中高一貫校受検 絶対合格！のために家族で頑張るブログ

日曜日に、今後どのように勉強するかを話し合ったのですが、
模試でどのように「困ったのか」を具体的にイメージしてもらうため、
１１月３日に受けた模試の問題を見て振り返ってもらいました。

【参考】　塾の面談　２人の先生から見た長男

「これとこれは解けた。最後の問題は時間切れだった。」と、自分なりの分析をしていました。
そして「時間がなくて焦った。」とも言っていました。

分かります。
時間のなさ、そして焦る気持ち。

分かりますが、あえて母は訊きます。
「なんで焦るのかなぁ？」

「全部解かなきゃと思うから・・・」という返事。

ここがトリッキーなんですよね。
学校のテストや、塾での簡単な確認問題は全部解くのが当たり前な訳です。
適性型の模試だと、全部解くのは時間的に無理。

そうなると、どの問題を解くのか、どれを捨てるのか、その判断が必要になります。
そうそう、判断の前に「全部解かなくてもいい」ということをしっかりと
理解してもらわないといけません＾＾

「全部解かなくてもいいんだよ。」

そう言うと、お兄ちゃんはノートに

　・全部解こうとしない

と書き込んでいました。

本当に分かっているかの確認をします。

「たとえば、試験の残り時間が３分だったとするよね？　手付かずの問題と途中まで解いた問題があったとして
　どちらを解けばいいと思う？」

「途中まで解いた問題？」

おお！理解した様子です＾＾


これは高校受験をした時に、私が塾の先生にさんざん言われたことです。
全部の問題に手をつける必要はない、と。

しかし実際は、高校受験（私立）の時、私は数学の問題を全て解きました。
受験生が多くて、私は体育館での受験となったのですが、寒かったせいか
お腹が痛くなってしまったのでした。

腹痛は返って私の集中力を呼び起こし、数学の問題を全て解くことにつながったのです。
でも、この話しはお兄ちゃんにはしません。
混乱しますからね＾＾；

後で塾の先生に「数学全部解きました！」と告げると、「なんで全部解くんだ！」って
怒られましたけれどもね。
受かったのですから、結果オーライです＾＾

おっと横道にそれました。


模試でも、なるべく本番に近い状態で受けて欲しいので、いろいろ戦略をたてています。

　適性１の場合、まずは問題文の出典（作者・タイトル）を見ます。
　次に設問文をさらっと読んで、どんな設問なのかを見ておきます。
　それから問題文を読んで、読解および作文にとりかかるのです。

　適性２の場合、大問１→大問３→大問２の順番で解くようにします。

　適性３の場合、算数は「わける・そろえる・ひろげる」で解くようにします。

これらが無意識レベルにできるようになったら、適性当日も焦ることなく、
戦えるんじゃないかと思います＾＾

「わける・そろえる・ひろげる」は、「算数は図で考えればグングン伸びる！」という本の
考え方です。
私立の算数の問題も、この本を読めば８割方解けるようになるそうです。
適性の算数でてこずっている方、おすすめです。

本質が分かっていれば、算数の問題もほとんど「型」で解けるんだなと
思わされます。
いろいろ問題集をやるより、この１冊を解く（というか読むというか＾＾）方が、
効率的に算数の点数を伸ばせると思います。

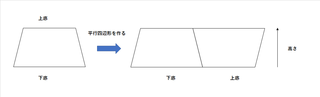
【参考】　台形の面積の公式がなぜそうなるのか？を考えてみよう


★算数は図で考えればグングン伸びる！

Amazon

算数は「図」で考えればグングン伸びる!―中学受験で驚異の合格実績

楽天

算数は「図」で考えればグングン伸びる！ 中学受験で驚異の合格実績 [ 橋本和彦 ]

↓ 記事がお役に立った場合、ぽちっと応援クリックをお願いします＾＾

人気ブログランキングへ



にほんブログ村