都立中高一貫校受検 絶対合格！のために家族で頑張るブログ

月曜日は塾の日なので、Ｅテレの「ニューベンゼミ」はお兄ちゃんは見られません。
録画して、木曜日の夜に見るというサイクルが出来て来ました＾＾

今週のお題は「“友だちと一緒”勉強法」です。
中学生や高校生になると、放課後学校に残って友だちと勉強ということが増えると思います。
でも、少し勉強しただけで、つい話し込んでしまったり、漫画を読み始めてしまったり・・・
それを回避するような方法を教えてくれます。


【参考】

　　効果バツグン！“友だちと一緒”勉強法


友だち同士で教えあうのも、双方にとって力になるので、おすすめな勉強法です。
小学生で友だち同士で教えあうことないし〜
そう思われるかもしれませんが、来春無事に公立中高一貫校に合格したら、
学校でアクティブラーニングが待っている訳です。
今のうちにお兄ちゃんにイメージさせておくのは、大事だと思いました＾＾

そして、ゼミ長の岡田結実ちゃんが台形の面積の公式の説明をするように言われて、
「えええ！！！」となりながらも、説明していました。
小学校で習う台形の面積の公式なのですが、改めて「なぜそうなるのか説明してみろ」と
言われたら、軽くパニックになるかもしれません。
実際、結実ちゃんもしどろもどろになり、ゼミ員のみんなから突っ込まれていましたから＾＾；

小学生も知っている公式なのでお兄ちゃんにも公式の説明をしてもらいました。
ホワイトボードに台形を書き、模範解答に近いであろう説明をしていました。

　もともとの台形に、上下を逆さにした台形を並べると、平行四辺形ができる。
　平行四辺形の面積は台形２つ分の面積と等しい。
　平行四辺形の面積は、「（上底＋下底）×高さ」で求めることができるから、
　台形ひとつ分の面積は「（上底＋下底）×高さ÷２」で求められる。

ここまでは、公立中高一貫校を目指す小６の子であれば、ほとんど子ができると思います。



↑文字だと分かりづらい（泣）という方のために、図形を書いてみました。
画像が見えづらい場合は、クリックすると大きく表示されます＾＾

公立中高一貫校受検生に求められるものは、別解力だと思います。
なので、「別解を考えてみよう＾＾」とお兄ちゃんに言ってみました。
台形の面積の別解なんて、想定外なので、思考力ストップのお兄ちゃんです。

母はヒントを出します。
台形の面積の公式をもし忘れてしまったら？
平行四辺形の公式が思い出せなかったら？
これは、ど緊張の中での入試もしくは適性試験であれば、ありうる話しです。

「どんなに緊張していても絶対に忘れない面積の公式は？」と訊くと
おそるおそる「三角形・・・？」と答えるお兄ちゃん。

そうです。三角形の面積の公式であれば、忘れることはないでしょう。
なので、三角形の面積の公式を使ったやり方を考えてみましょうか。

図形問題と言えば、補助線です。
これは以前買った「算数は『図』で考えればグングン伸びる！」にも書かれている通り、
補助線を引いて考えることになります。



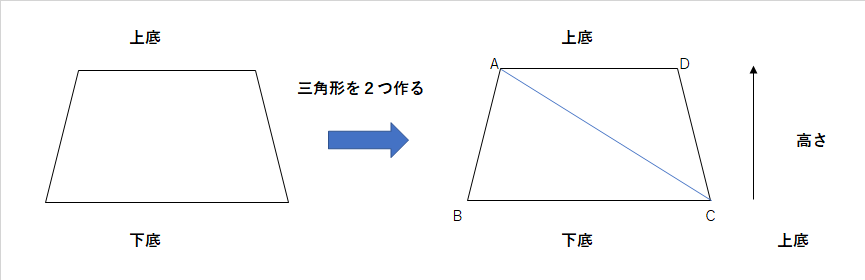
↑こんな感じで、台形ＡＢＣＤの頂点Ａから頂点Ｃに補助線を引きます。
すると、台形ＡＢＣＤは、三角形ＡＢＣと三角形ＡＣＤに分けることができます。
この２つの三角形の面積の和を求めれば、台形の面積が求められることになります。

三角形の面積の公式はというと、「底辺×高さ÷２」です。
よって、三角形ＡＢＣの面積は「辺ＢＣ×高さ÷２」（下底×高さ÷２）になります。
同様に、三角形ＡＣＤの面積は「辺ＡＤ×高さ÷２」（上底×高さ÷２）になります。

以上のことから、台形ＡＢＣＤの面積は三角形ＡＢＣと三角形ＡＣＤの面積の和となり、

　辺ＢＣ×高さ÷２＋辺ＡＤ×高さ÷２＝（辺ＢＣ＋辺ＡＤ）×高さ÷２
＝（下底＋上底）×高さ÷２＝（上底＋下底）×高さ÷２

台形の面積が導き出されるという訳です。


実際の適性で台形の面積が出るかどうかは分かりませんが、
以前都立の適性検査で、円の面積がなぜ「半径×半径×３．１４」になるのか？
という問題が出たことがあるそうなので、やっておいて損はないなと思いました。

誰も助けてくれない、１２歳の孤独な戦いの適性検査。
公式を度忘れしてしまったらどうしたらいいのか！？ということを、
別解を考えさせて、生き残るための戦略として教える母でした＾＾

ヒントを出せば、別解を考えられるお兄ちゃんですが、これが一人でできるようになってくれるといいなぁと
思うのでした。

図形問題は苦手・・・なお子さまをお持ちの方、下記の本は保護者必読の本です。
本質が分かっていれば、図形問題は正直こわくないです。
苦手を一緒に克服しようではありませんか＾＾！！


★算数は図で考えればグングン伸びる！

Amazon

算数は「図」で考えればグングン伸びる!―中学受験で驚異の合格実績

楽天

算数は「図」で考えればグングン伸びる！ 中学受験で驚異の合格実績 [ 橋本和彦 ]

↓ 記事がお役に立った場合、ぽちっと応援クリックをお願いします＾＾

人気ブログランキングへ



にほんブログ村