パプリカ2020の部屋

この広告は30日以上更新がないブログに表示されております。
新規記事の投稿を行うことで、非表示にすることが可能です。

暦を作ることにより自然現象を予測して生活することができるようになりました。
暦を作る原動力は月の周期的な満ち欠けと、季節は変化するものの一定のパターンがあることに気づいたことです。

これは太陽と地球と月の関係性で生まれた周期性に基づくものでした、
地球の場合は、公転周期と自転周期が違うので1日ができました。自転軸が公転面に対して適度に傾いていたので季節が廻り1年ができました。

地球と異なる自転軸をもった惑星の1日とか1年はどのようになるのでしょうか？

自転周期と公転周期が同じとき永遠に太陽は空の一点に留まることになります。
公転周期と自転周期が違うのですが、自転軸が公転面に垂直のとき季節は生まれず1年を太陽の動きで認識することはできません。夜の星空を観測して1年を知ることになります。

自転軸が公転面と一致しているとき、1年の半分は太陽が沈まず空の真上を中心に動いています。春は地平線に沿って太陽は一周するとそれが1日なのです。夏に近づくにつれて太陽がまわる位置は上昇し、夏至の日は太陽は頭上の一点に留まり動かなくなります。この日から秋に向かって太陽の高度が下がってきて秋〜冬の境目で太陽は春のときと同じように地平線に沿って一周して、やがて地平線の下に沈んでいくのです。冬の始まりです。夕暮れのような日にちが続いたのち地上は闇に包まれます。夜空には満点の星が輝くのです。

このような惑星の住人はどのような暦を作るのか、想像するとワクワクします。

x^2−x＋1＝0・・・�@　の解をα
x^2＋x−1＝0・・・�A　の解をβ
〜〜〜〜〜〜〜〜〜〜〜
１　αβを解に持つ4次方程式をひとつ
２　その４解の平方の和


あっさりα、βと書いてありますが、２次方程式の解なので解は2づつあります。
α→a、b
β→m、n
と4つの解を置きます。

�@と�Aを4つの解のa、b、m、nで表すと
�@は（x−a)(x−b）＝0
�Aは（x−m)(x−n）＝0　です。

�@は
x^2−（a＋b)x＋ab＝x^2−x＋1＝0　ですから
a＋b＝1
ab＝1　です。

�Aは
x^2−（m＋n)x＋mn＝x^2＋x−1＝0　ですから
m＋n＝−1
mn＝−1　です。

さて、「αβを解にもつ」ですから
解は、am、an、bm、bnの4つです。
したがって「αβを解に持つ4次方程式をひとつ」を
（x−am)(x−an)(x−bm)(x−bn）＝0　とします。

これは、
（x^2−a(m＋n)x＋a^2mn)(x^2−b(m＋n)x＋b^2mn）＝0　
ここで　m＋n＝−1、mn＝−1　ですから、上の式は

（x^2−a(−1)x＋a^2(−1))(x^2−b(−1)x＋b^2(−1)）＝0　
したがって
（x^2＋ax−a^2)(x^2＋bx−b^2）＝0

引き続きこれを展開します。
x^2(x^2＋bx−b^2)＋ax(x^2＋bx−b^2)−a^2(x^2＋bx−b^2）＝0

どんどん展開します。
x^2･x^2＋bx･x^2−b^2･x^2＋x^2･ax＋bx･ax−b^2･ax−x^2･a^2−bx･a^2＋b^2･a^2＝0

x^4＋bx^3−b^2x^2＋ax^3＋abx^2−ab^2x−a^2x^2−a^2bx＋a^2b^2＝0

x^4　＋ax^3＋bx^3　−a^2x^2−b^2x^2＋abx^2　−a^2bx−ab^2x　＋a^2b^2＝0

x^4　＋(a＋b)x^3　−(a^2＋b^2−ab)x^2　−ab(a＋b)x　＋(ab)^2＝0

「a^2＋b^2＝a^2＋2ab＋b^2−2ab＝(a＋b)^2−2ab」　だから
x^4　＋(a＋b)x^3　−((a＋b)^2−2ab−ab)x^2　−ab(a＋b)x　＋(ab)^2＝0

ここで
a＋b＝1、ab＝1　ですから
x^4　＋(1)x^3　−((1)^2−2−1)x^2　−1(1)x　＋(1)^2＝0

したがって
x^4＋x^3＋2x^2−x＋1＝0　となります//


次に
「その４解の平方の和」ですから
(am)^2＋(an)^2＋(bm)^2＋(bn)^2　を求めます。

これは
a^2(m^2＋n^2)＋b^2(m^2＋n^2)
＝(a^2＋b^2)(m^2＋n^2)
＝((a＋b)^2−2ab)((m＋n)^2−2mn)

ここで、
a＋b＝1、ab＝1、m＋n＝−1、mn＝−1　ですから

((a＋b)^2−2ab)((m＋n)^2−2mn)
＝((1)^2−2)((−1)^2−2(−1))
＝(−1)・(＋3)
＝−3//　です。

途中で計算間違いがあったらごめんなさい。
考え方はいい感じだと思いますので。

暇つぶしゲームのその2は、「旅かえる」。お弁当と旅支度をしておくと、勝手に旅に出て記念写真やお土産をもって帰ってくるという、ゆるいゲームです。
しばらくアクセスを忘れていてもお弁当を持たせていなくとも勝手に旅に行ってきます。写真もお土産ももって帰ります。ただし旅支度したときよりもしょぼい写真やお土産になってしまいます。



旅カエルの自宅前には「お金」として使える葉っぱが生えてきます。適宜収穫して、店屋でお弁当や必需品を買います。お弁当の他、テントや器、灯り、手ぬぐい、水筒、マフラーを買って、旅支度をしてあげます。
旅の安全に必要なお守りも持たせます。定番の四つ葉のクローバーです。ほかにお店の福引て当てたお守りもあります。


お弁当はサンドイッチを持たせることが多いです。お手頃な値段です。



旅から帰ると旅カエルは自宅で旅の思い出なんぞを記録しているようです。ツアーライターなのかもしれません。


今まで旅先で撮ってきた記念写真を２・３枚紹介します。
浅草雷門

姫路城
白川郷

天橋立

他にもいろいろなところを旅してます。旅の行き先は国内限定のようです。

通勤電車での時間の過ごし方について、ほとんどはYOUTUBEでヨビノリの動画を見る、ストリートピアノを聴く、というものです。そのほかにゲームをします。ゲームといっても、「デジタルぬり絵」と「勝手に旅して帰ってくるカエル」のゲームです。これはゲームといえるのでしょうか？



画像左がディジタルぬり絵ゲームのHappyColorです。
ゲームを開始すると、輪郭線に数字が入った図柄が表示され、好きなものを選択できるようになっています。ちなみに毎日新しい図柄がアップされます。



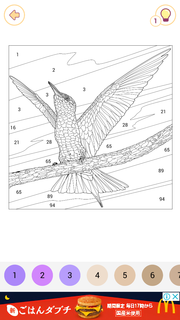
図柄は動物、植物、静物、人物等様々です。
いま、鳥の絵を選択しました。



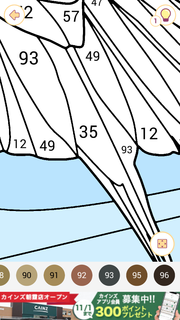
拡大縮小ができます。下のパレットから数字のついた色をタッチして選択します。輪郭線の中に表された数字と選んだ色の数字が一致した部分にチェック模様が入って分かりやすくなっています。この部分をタッチすると、選択した色に塗られます。

完成したぬり絵です。





↓ちなみに、ディジタルぬり絵の中で一番のお気に入りの絵です。

地球圏外に探査機を飛ばすようになって随分と経ちますが、太陽系内惑星では未だに生命の痕跡すら発見されていません。
もう少し詳しく調べていったら、いずれ発見されるだろうという楽観的な見方と、もはや太陽系内で生命が生まれたのは唯一地球だけじゃないのか、という悲観的な見方が交錯しています。

それまで暗幕の小さな穴から漏れる光の点だと思っていた夜空に輝く星々が、実は太陽にように自ら光り輝く恒星だということが分かったのは、恒星から届く光をスペクトルに分解して調査研究できるようになった19世紀中頃以降です。
しかし、恒星は太陽と同じように自ら輝いていることが分かっても、太陽と同じように惑星をもっているかどうかは分かりませんでした。

ところが、1995年にスイス・ジュネーブ大のミシェル・マイヨールとディディエ・ケローが、ペガスス座51番星の周りをわずか4.2日の周期で公転する惑星を発見しました。それ以降、現在までに約3000個以上の太陽系外惑星が発見されています。今では、太陽に似た恒星のほとんどは惑星をもつことが分かっています。

恒星が誕生すればその周囲に必然的に惑星系ができることまでは分かりました。惑星系ができれば、必然的とまではいわなくとも生命が誕生した惑星があってもいいのではないか、とまでは思うようになりました。

いろいろ思いを巡らせるのは自由ですが、今のところ生命が住んでいると言えるのは地球だけなのです。太陽系の惑星探査も進展し、同様に系外惑星の観測も進化し、生命の兆候を捉える日がくるかもしれません。
しかし、その日が来るまでは、生命を宿していると断言できる星は宇宙で地球が唯一で無二なのです。

＊ちなみに、ミシェル・マイヨール(写真左)とディディエ・ケロー(写真右)は「太陽と似た恒星の周りを公転する系外惑星の発見に対して」2019年のノーベル物理学賞を受賞しました。

先日、通勤電車でYOUTUBEのヨビノリ見て乗り越してしまったので、今朝は乗り越さないようにストリートピアノの方を見ていました。次の視聴候補がいくつもあるなかで大阪桐蔭吹奏楽部の動画ががいくつかありました。そこで吹奏楽で「紅蓮華」を聴いてみました。ふむふむ。

次に「13期生卒業公演」を聴いてみました。Official 髭男 dism メドレーです。
よく見ると、観客席がスッキリしています。というか無観客でした。卒業公演が無観客とは、コロナ禍はこんなところにも影響がでているんですね。卒業生にとってはとても残念なことだったでしょう。

コメントに「世界一受けたい授業ではちょっとしか放送されなかったのに、フルで見られるなんてほんとに幸せです…！！　
ありがとうございますヽ( ´▽｀)ノ」

テレビに取り上げられていたんですね。

この動画は2020年4月にアップされていて6か月で100万回再生されています。
↓　　　↓　　　↓
https://www.youtube.com/watch?v=dsb-nZScHmg


吹奏楽は大阪桐蔭だけじゃないことを心せなアカン。吹奏楽でアップされている動画を全部見たい。

夏休みの宿題帳には自由研究のページがあって、夏休み明けには全員が発表させられました。
「アリの研究」と「サビの研究」が小学校の夏休みの自由研究の定番でした。

「アリの研究」のテーマは、アリは何色が好きか？というもです。色紙に砂糖水を塗って、どの色を好んで集まってくるのかを調べました。（アリはそもそもモノを見て行動しているのか？アリはそもそも色が見分けられるのか？という疑問はわかず、したがって事前にそのことについ調べることはしません。思いついたら即、実験です）

長時間観察しているのがめんどくさいので、ハエトリガミ（ハエトリリボン：下記URL参照）をハサミで2cm四方くらいに切って、ゴキブリホイホイ的にアリを捕まえて、最終的にハエトリガミに引っ付いたアリの数を数えようと企みました。
http://www.tt-techno.co.jp/gyoumu_seihin2/76-38.html

ところが、このハエトリガミの粘着力は半端なくて、しかもべとべとで、色紙に張り付けるどころではなくなってしまい、当初の目論見は外れたうえに、手やハサミについた粘着物質を洗い落とすのに大変でした。

「サビの研究」は次の通りです。
夏休みが始まると、釘を「真水」と「塩水」と「砂糖水」に入れて、夏休みが終わるころに、どの釘が一番サビているかを観察するのです。途中経過は観察しないのでとても楽な研究でした。夏休み明けに、どの釘が一番サビたかを報告したところ、クラスの同級生から質問を受けましたが、分かりませんと答えて終わりました。
アリの時と同じように、その先を突っ込んで調べたりはしなかったのです。

しかたなくやる研究なんてこんなもんでしょう。

今は、他人から与えられた夏休みの宿題帳はありませんが、日ごろ不思議だと思ったことなどWikipediaなんぞで調べたり、自分で検算をしてみたり、関連する本を買って読んでみたりと、わりと「自由研究」っぽいことしています。

1976年11月2日、超音速旅客機コンコルドの製造中止が決定した日です。

超音速旅客機はアメリカや旧ソ連でも開発していました。就役したのは、イギリスとフランスで共同開発したコンコルドと、旧ソ連が開発したTu-144で、アメリカはボーイング社等が開発していましたが米国政府からの研究助成金が打ち切られたことにより、開発が頓挫しました。

コンコルドは、1976年1月21日に運用開始、2003年10月24日に最後の営業飛行を終えました。一方、Tu-144は1975年12月26日営業運行開始、これはコンコルドよりも1ヶ月早いものでしたが、1978年6月6日に運航が中止になっています。

超音速旅客機のばら色の未来、
「1機あたりの生産性が倍」、「航空会社の保有する機体の数を半減」、「大西洋間の日帰り旅行が可能」「乗客にとっては世界をより小さくするもの」「将来的には商用旅客機のほとんどは超音速輸送機になるだろう」。

超音速旅客機が直面した壁、
技術的には、「ソニックブームによる地上への被害」「高空での排気ガスがオゾン層を破壊」、
商業的には、「時代は長距離大量輸送時代に突入し400人以上を同時に輸送できるボーイング747に対し100名程度のコンコルドは太刀打ちできなくなった」「ターボジェットエンジンからターボファンエンジンの時代になり低騒音、低燃費を実現、このターボファンエンジンは超音速機には使えないので、騒音問題、燃費問題がますます大きくなった」「燃費の問題は1980年代のオイルショックで決定的となった」。

オイルショックを経験する前にすでに採算が合わないことが分かったということです。
結果的にアメリカは良い選択をしたことになります。

YOUTUBEを見ていたら面白い問題を見つけました。
某有名企業の入社試験問題だそうです。
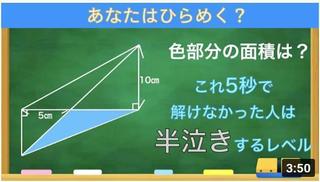
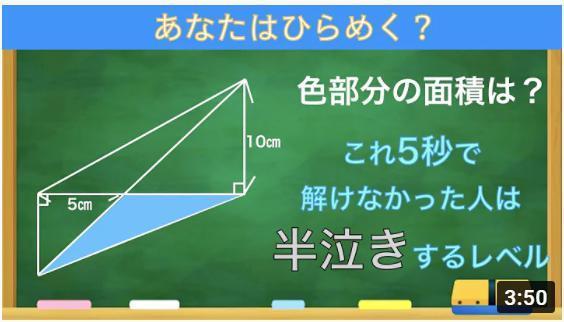
「Ｑ．次の図形の面積を求めよ」


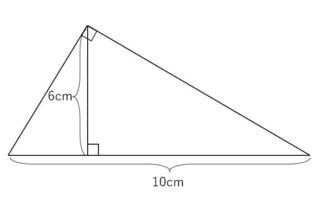
見た瞬間「底辺×高さ÷2」で完璧。30平方ｾﾝﾁﾒｰﾄﾙ。
この答えは間違いだそうです。・・・え？計算は合ってるじゃあないですか（怒！

正解は「このような三角形は存在しない」だそうです。
ん？？？
10cmの底辺を直径として、三角形が直角を持つ頂点をとおる円を描きます。


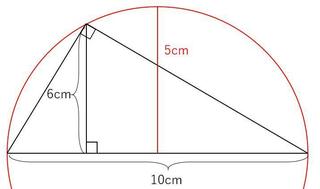
この三角形の高さにあたる部分は、どうがんばってもこの円の半径より小さくなります。この円の半径は直径÷2で、10cm÷2＝5cmですから、高さが6cmの三角形にはなりえないのです。


YOUTUBEでは別の方法で説明していました。

要は、入社試験に小学生でも解ける問題を出すことから疑え、問題という前提を疑え、というものでした。

ひとを騙す時はこのようなありもしない前提をさもあるように始めるのがコツかもしれません。前提から始まるわけですからそれ以降の筋道は整然とするはずです。
オレオレ詐欺も「電話をしてきたのは息子だ」という前提を作り出すために、事前に小芝居を打つのです。

ひところ、地図が読めない女、などという失礼な題名をつけた本が売れましたが、商業ベースで売るために炎上ギリギリのネーミングだとは思います。

しかし、車ではGPS搭載のナビゲーションが発達して、地図を見なくても画面に指示された矢印通り、音声ガイダンス通りにハンドルを切れば目的地に着くようになりました。

歩きでも、スマホの地図アプリは現在地と目的地の間を矢印で案内して、車と同じように指示通り進むとOKなわけです。

こうなると、紙ベースの地図を読めなくなりますし、紙地図はますます売れなくなりますし、というスパイラルに陥って、結局は男も女も関係なく地図が読めなくなっています。

地図が読めない原因の一番の理由が、自分が今どこにいるのかが地図上で分からないというものでしょう。２番目として、地図の上下と実際の南北が分からない。そして３番目は地図の縮尺が分からない、というものだと思います。さらに自分がやりたいことと地図の特性がマッチしているのかも問題です。

市内の美味しいと噂のケーキ屋さんのことを聞いたが場所を知らない。住所を聞いて地図で場所を探そうとしたとき、まさか世界地図は広げないでしょう。（グーグルアースならやりかねませんがどんどん絞り込んでいくことはできます。この便利機能が地図を選べなくしているのかもしれません。）

アメリカにお金が無くなってGPS衛星の維持ができなくなったとき、世界は文字通り右も左も分からない暗黒の世界となるのです。