�V�K�L���̓��e���s�����ƂŁA��\���ɂ��邱�Ƃ��\�ł��B
�L��
�V�K�L���̓��e���s�����ƂŁA��\���ɂ��邱�Ƃ��\�ł��B
posted by fanblog
2020�N11��19��
�������y
���ɕs���ǂł͂Ȃ��̂ł��������Ȃ鉹�y��YOUTUBE�Œ����Ȃ���Q�Ă��܂��B�S���₩�ɂȂ鉹�y�Ƃ���Ƀ}�b�`�����C���X�g�Ŕ���������Ă����悤�ł��B�Ǐ������BGM�ɗǂ���������܂���B�����Q�������S�z�ł��B
https://youtu.be/ycUyDupmgZk

���̐������y���O�͒g�F�╰���A��̐�������鉹�̉f���𗬂��Ă��܂����B������ɂ��Ă��Z����2���ԁA������10���Ԉȏ�ɋy�ԉf�����A�b�v���[�h����ЂƂ�����̂ł��̂悤�ȑ̌����ł���̂ł��B
https://youtu.be/hcY-Ft8HB1Q

���̉f������������A�b�v����Ă���̂͂��ꂾ�����v�������Ƃ������Ƃł��B
https://youtu.be/ycUyDupmgZk

���̐������y���O�͒g�F�╰���A��̐�������鉹�̉f���𗬂��Ă��܂����B������ɂ��Ă��Z����2���ԁA������10���Ԉȏ�ɋy�ԉf�����A�b�v���[�h����ЂƂ�����̂ł��̂悤�ȑ̌����ł���̂ł��B
https://youtu.be/hcY-Ft8HB1Q

���̉f������������A�b�v����Ă���̂͂��ꂾ�����v�������Ƃ������Ƃł��B
�y���̃J�e�S���[�̍ŐV�L���z
-
no image
posted by �p�v���J2020 at 03:00| �i�J�e�S���Ȃ��j
2020�N11��18��
������������
��łɂȂ��đ��l�̗L�v�ȏ����ɔ������Ȃ��Ȃ�����A���̒��̌��ȃj���[�X�������Ȃ��ꍇ�ɁA�����ǂ����Ƃ������Ȃ�܂��B�u���`���A�����������ʂ́v�Ǝ��㌀���̂��㊯�l�������Ƃ��́A�����̈ӌ�������l�̋��݂��ɉ����t����Ƃ��ɐ邤�䎌�ł��B
���āA���Ȃ��ƂɎ����ǂ��ł���܂��ƁA���������Ȃ錻�ۂǂ����܂��B���ʊW�͑S������܂���B�����A���̂悤�ɍl����ЂƂ�����̂ł��B
���ɏW�����Ă�����A�Ǐ��ɏW�����Ă���ƁA���͂̉����S�������������Ȃ�܂��B���m�C�Y�L���Z���@�\�̕t�����w�b�h�t�H�����Ă��܂����A���̔�ł͂Ȃ����炢�����Ɏ��͂̉����������Ȃ��Ȃ�̂ł��B
�Ƃ���ł��̃m�C�Y�L���Z���@�\�̕t�����w�b�h�t�H���ł����A�Z�p�����������u�����������ʁv���u�Ƃ�����ł��傤�B
�Ђ����玩���̐��E�ɐZ���̂ł��B���̃w�b�h�t�H���ʼn��y���Ȃ���O������āA�N���N�V�����ɋC�Â����ɎԂ�瀂���Ȃ��悤�ɂ��܂��傤�B

���āA���Ȃ��ƂɎ����ǂ��ł���܂��ƁA���������Ȃ錻�ۂǂ����܂��B���ʊW�͑S������܂���B�����A���̂悤�ɍl����ЂƂ�����̂ł��B
���ɏW�����Ă�����A�Ǐ��ɏW�����Ă���ƁA���͂̉����S�������������Ȃ�܂��B���m�C�Y�L���Z���@�\�̕t�����w�b�h�t�H�����Ă��܂����A���̔�ł͂Ȃ����炢�����Ɏ��͂̉����������Ȃ��Ȃ�̂ł��B
�Ƃ���ł��̃m�C�Y�L���Z���@�\�̕t�����w�b�h�t�H���ł����A�Z�p�����������u�����������ʁv���u�Ƃ�����ł��傤�B
�Ђ����玩���̐��E�ɐZ���̂ł��B���̃w�b�h�t�H���ʼn��y���Ȃ���O������āA�N���N�V�����ɋC�Â����ɎԂ�瀂���Ȃ��悤�ɂ��܂��傤�B

posted by �p�v���J2020 at 03:00| �i�J�e�S���Ȃ��j
2020�N11��17��
���Z�������(���w1��)�������܂���
�������̖�肪�悤�₭�����܂����B

�������Ă����͉̂��}�̖��ł����B
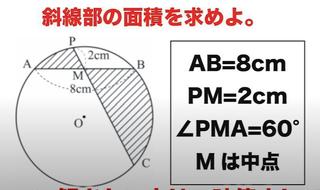
�܂��A���w���w�͉����܂ł��A�����ɂ߂܂��B
�~���p�ƒ��S�p�̊W��OK�B�O�����̒藝��OK�B���ʂȎO�p�`�i���p�A60���A30���j�y�юO�p�`�i���p�A45���A45���j�̕ӂ̔��OK�B�}�`�̑�����OK�B�~�����̓�OK�B�Ƃ������ƂŁA�v�Z���n�߂܂��B
�}���̒����̒P�ʂ�cm�ł����A�ȉ��ł͒P�ʂ��O���Đ������Ă����܂��B
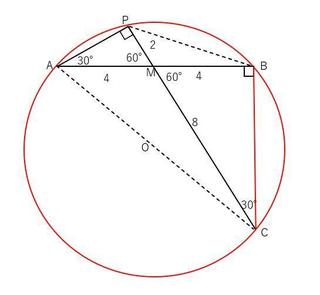
��AMP�ɂ����āA�Q�ӂɋ��܂ꂽ�p��60���ŁA�ӂ̔䂪1�F2�ł��邱�ƂɋC�t���܂��B
����́A��60���A��30���A��90���̊p�x�������p�O�p�`�ł��B���������āA�Ε�AP��2sqrt(3)�ƌv�Z�ł��܂��B
��AC�̉~���p�ł����APC�����p�Ȃ̂ŁA����AC�͂��̉~�̒��a�ɂȂ�܂��B
�܂���ABC����AC�̉~���p�Ȃ̂Œ��p�ɂȂ�܂��B
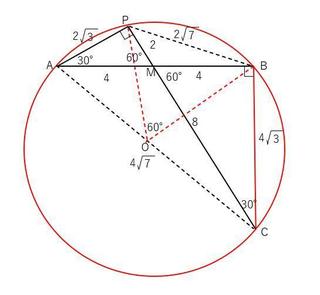
���ɁA��AMP����CMB��60���ł���A��APM����CBM��90���Ȃ̂ŁA��AMP�䇙CMB�ł��̔��1�F2�ł��B���������āA��BC��4sqrt(3)�ł��B
���p��ABC�ɂ����ĎO�����̒藝���A�~�̒��aAC�����܂�܂��B
AC��sqrt(8^2�{4^2×3)��4sqrt(7)�ł��B
��PB�̉~���p��PAB��30���Ȃ̂ŁA���S�p��60���ɂȂ�܂��B
���������ć�POB�͈�ӂ̒������~�̔��a�ɓ����������̐��O�p�`�ł��B
��`POB�̖ʐς͉~�̖ʐς�1/6�ɂȂ�܂��B
��`POB�̖ʐρ�(2sqrt(7))^2×��/6��28��/6��(14/3)��
���O�p�`POB�̖ʐρ�2sqrt(7)×sqrt(21)/2��7sqrt(3)
����āA��PB�Ɛ���PB�ň͂܂ꂽ�����̖ʐ�S1��(14/3)��-7sqrt(3)
���ɁA��PMB�̖ʐρ���AMP�̖ʐρ�S2�i��ӂ�4�œ������A�������������j
�䂦�ɁAS2��2×2sqrt(3)/2��2sqrt(3)
�܂��A��AMC�̖ʐρ���CMB�̖ʐρ�S3�i��ӂ�4�œ������A�������������j
�䂦�ɁAS3��4×4sqrt(3)/2��8sqrt(3)
���������ċ��߂�ʐς́A
���~�̖ʐς���AS1�{S2�{S3���������܂�܂��B
���~�̖ʐρ�14�Ȃ̂ŁA���߂�ʐς�S�Ƃ����S��14�|(S1�{S2�{S3)�ł��B
���ꂼ��ɐ��l���������
S��14�|((14/3)��-7sqrt(3)�{2sqrt(3)�{8sqrt(3))
�@��(28/3)�|3sqrt(3)
�P�ʂ�߂��Ƌ��߂�ʐς�
( (28/3)�|3sqrt(3) ) cm^2
�ƂȂ�܂��B
���f�^�V�߂ł���
�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`
�������Z�������ŕ������ł��B

�Ƃ��������T���Ă��܂��B
�@4^24�@���@5^24�@���@6^24�@���@8^24
�@(2^2)^24��2^48�@���@2^48�@���@5^24
�@8^24��(2^3)^24��2^72�@���@5^24�@���@2^72
�������ł��B

�������Ă����͉̂��}�̖��ł����B

�܂��A���w���w�͉����܂ł��A�����ɂ߂܂��B
�~���p�ƒ��S�p�̊W��OK�B�O�����̒藝��OK�B���ʂȎO�p�`�i���p�A60���A30���j�y�юO�p�`�i���p�A45���A45���j�̕ӂ̔��OK�B�}�`�̑�����OK�B�~�����̓�OK�B�Ƃ������ƂŁA�v�Z���n�߂܂��B
�}���̒����̒P�ʂ�cm�ł����A�ȉ��ł͒P�ʂ��O���Đ������Ă����܂��B

��AMP�ɂ����āA�Q�ӂɋ��܂ꂽ�p��60���ŁA�ӂ̔䂪1�F2�ł��邱�ƂɋC�t���܂��B
����́A��60���A��30���A��90���̊p�x�������p�O�p�`�ł��B���������āA�Ε�AP��2sqrt(3)�ƌv�Z�ł��܂��B
��AC�̉~���p�ł����APC�����p�Ȃ̂ŁA����AC�͂��̉~�̒��a�ɂȂ�܂��B
�܂���ABC����AC�̉~���p�Ȃ̂Œ��p�ɂȂ�܂��B

���ɁA��AMP����CMB��60���ł���A��APM����CBM��90���Ȃ̂ŁA��AMP�䇙CMB�ł��̔��1�F2�ł��B���������āA��BC��4sqrt(3)�ł��B
���p��ABC�ɂ����ĎO�����̒藝���A�~�̒��aAC�����܂�܂��B
AC��sqrt(8^2�{4^2×3)��4sqrt(7)�ł��B
��PB�̉~���p��PAB��30���Ȃ̂ŁA���S�p��60���ɂȂ�܂��B
���������ć�POB�͈�ӂ̒������~�̔��a�ɓ����������̐��O�p�`�ł��B
��`POB�̖ʐς͉~�̖ʐς�1/6�ɂȂ�܂��B
��`POB�̖ʐρ�(2sqrt(7))^2×��/6��28��/6��(14/3)��
���O�p�`POB�̖ʐρ�2sqrt(7)×sqrt(21)/2��7sqrt(3)
����āA��PB�Ɛ���PB�ň͂܂ꂽ�����̖ʐ�S1��(14/3)��-7sqrt(3)
���ɁA��PMB�̖ʐρ���AMP�̖ʐρ�S2�i��ӂ�4�œ������A�������������j
�䂦�ɁAS2��2×2sqrt(3)/2��2sqrt(3)
�܂��A��AMC�̖ʐρ���CMB�̖ʐρ�S3�i��ӂ�4�œ������A�������������j
�䂦�ɁAS3��4×4sqrt(3)/2��8sqrt(3)
���������ċ��߂�ʐς́A
���~�̖ʐς���AS1�{S2�{S3���������܂�܂��B
���~�̖ʐρ�14�Ȃ̂ŁA���߂�ʐς�S�Ƃ����S��14�|(S1�{S2�{S3)�ł��B
���ꂼ��ɐ��l���������
S��14�|((14/3)��-7sqrt(3)�{2sqrt(3)�{8sqrt(3))
�@��(28/3)�|3sqrt(3)
�P�ʂ�߂��Ƌ��߂�ʐς�
( (28/3)�|3sqrt(3) ) cm^2
�ƂȂ�܂��B
���f�^�V�߂ł���
�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`
�������Z�������ŕ������ł��B

�Ƃ��������T���Ă��܂��B
�@4^24�@���@5^24�@���@6^24�@���@8^24
�@(2^2)^24��2^48�@���@2^48�@���@5^24
�@8^24��(2^3)^24��2^72�@���@5^24�@���@2^72
�������ł��B
posted by �p�v���J2020 at 03:00| �i�J�e�S���Ȃ��j
2020�N11��16��
�]��
�J�~�I�J���f�Œ��V�������̃j���[�g���m���ϑ�����2002�N�m�[�x�������w�܂���܂������ď��r�����S���Ȃ��܂����B
�d���Ő��ɒP�g���C���Ă������A���k��w����Â��Ă���T�C�G���X�E�J�t�F�ł��b�������Ƃ�����܂��B�m�[�x����҂̂��b�ɕ�����`�����X�͐l���ɗL�邩�������Ȃ̂łƂĂ���ۂɎc���Ă��܂��B
�J�~�I�J���f�͗z�q������ϑ����邽�߂Ɍ��݂���܂������A�܂��z�q������ϑ��ł��Ă��Ȃ��Ǝv���܂��B����͗z�q�̎������\�z����Ă�������y���ɒ����Ƃ������Ƃł��傤�B�Ƃ������Ƃ́A�F���̏I���͂���ɐ�ɂȂ����̂ł��B�����N��H
�J�~�I�J���f����o�[�W�����A�b�v�����X�[�p�[�J�~�I�J���f���g���ăj���[�g���m�U�������������c���͎���2015�N�x�̃m�[�x�������w�܂���܂��Ă��܂�
�X�[�p�[�J�~�I�J���f�͂���Ȃ�o�[�W�����A�b�v���ăn�C�p�[�J�~�I�J���f�ƂȂ�2027�N�ɉғ��\��ł��B

�� ���c���A�E �����i�Y�o�j���[�Xweb��2015.10.6�j

�X�[�p�[�J�~�I�J���f
�d���Ő��ɒP�g���C���Ă������A���k��w����Â��Ă���T�C�G���X�E�J�t�F�ł��b�������Ƃ�����܂��B�m�[�x����҂̂��b�ɕ�����`�����X�͐l���ɗL�邩�������Ȃ̂łƂĂ���ۂɎc���Ă��܂��B
�J�~�I�J���f�͗z�q������ϑ����邽�߂Ɍ��݂���܂������A�܂��z�q������ϑ��ł��Ă��Ȃ��Ǝv���܂��B����͗z�q�̎������\�z����Ă�������y���ɒ����Ƃ������Ƃł��傤�B�Ƃ������Ƃ́A�F���̏I���͂���ɐ�ɂȂ����̂ł��B�����N��H
�J�~�I�J���f����o�[�W�����A�b�v�����X�[�p�[�J�~�I�J���f���g���ăj���[�g���m�U�������������c���͎���2015�N�x�̃m�[�x�������w�܂���܂��Ă��܂�
�X�[�p�[�J�~�I�J���f�͂���Ȃ�o�[�W�����A�b�v���ăn�C�p�[�J�~�I�J���f�ƂȂ�2027�N�ɉғ��\��ł��B

�� ���c���A�E �����i�Y�o�j���[�Xweb��2015.10.6�j

�X�[�p�[�J�~�I�J���f
posted by �p�v���J2020 at 03:00| �i�J�e�S���Ȃ��j
2020�N11��15��
�C����ꂩ�����Ƃ�
���̌C�Ɗ������ƐS���������̂ł����A���̂ق��͂��������䖝���āA�C���ǂ��ɂ����悤�ƍl���܂����B�����āA�u�Ԑڒ��܂��Ă��܂����B�����Z�ݍ���ł���Ƃ�����u�Ԑڒ��܂Ŗ��߂�̂ł��B500�~�̏u�Ԑڒ��܂łǂ��܂őΉ��ł���̂��A�������l�͂���܂��B
���p�r�A�����ڒ���搂�����̃A�����A���t�@�[���[��EXTRA�B�v���X�`�b�N�A�����S���A�����A�؍ށA����A�v�A�Ɏg���܂��B�C�͐l�H��v�Ȃ̂Ō����̂����s���ł����B�E�̌C�̐�[��������Ă����̂ŁA��������ڒ��܂����݂��܂��܂����B

��P���ځA���������B���͐Z�ݍ��܂��A�C�����̗ǂ��ʋ��ł��܂����B�J�̓��̗J�T���������H
��Q���ځA����A�e�w�̕t��������Z�ݍ���ł��܂����B�C�̐�[�������ꂩ���Ă��������͔�Q�͏������̂ł����A����ł��C���̓o�b�h�����B
�E�C�̐e�w�̊O���̂���������Ă݂܂��ƁA�C��ꂽ�悤�ɂȂ��Ă��āA��������C�̒��̕��������܂����B�ڒ��܂ŕ�C���邷�ׂ�������Ȃ������̂ŁA�Ƃ肠������ڂ������Ă��镔���ɉ����Ăׂ��ׂ��h���Ă݂܂����B���̂Ƃ�������Ă������ł��B
�ڒ��܂������Ď��͂̂��̂Ƃ����ꍇ���悤�ɂȂ�ƁA�ڒ��܂�h�����Ƃ��낪���݂�ттĂ��܂����B�����C�ɔ��̔��_�݂͂��Ƃ��Ȃ��̂ŁA����͌C�n��h���č������悤�Ǝv���A�C�n���Ă���Ƃ����T�����̂ł����A�ӊO�Ƌߏ��ɔ����Ă���X�������̂ł��B
���������Ȃ��̂Ńl�b�g�ŒT���̂ł����A�C�n���A�}�]���ŒT���悤�ɂȂ�Ƃ͎v�������܂���ł����B
���p�r�A�����ڒ���搂�����̃A�����A���t�@�[���[��EXTRA�B�v���X�`�b�N�A�����S���A�����A�؍ށA����A�v�A�Ɏg���܂��B�C�͐l�H��v�Ȃ̂Ō����̂����s���ł����B�E�̌C�̐�[��������Ă����̂ŁA��������ڒ��܂����݂��܂��܂����B

��P���ځA���������B���͐Z�ݍ��܂��A�C�����̗ǂ��ʋ��ł��܂����B�J�̓��̗J�T���������H
��Q���ځA����A�e�w�̕t��������Z�ݍ���ł��܂����B�C�̐�[�������ꂩ���Ă��������͔�Q�͏������̂ł����A����ł��C���̓o�b�h�����B
�E�C�̐e�w�̊O���̂���������Ă݂܂��ƁA�C��ꂽ�悤�ɂȂ��Ă��āA��������C�̒��̕��������܂����B�ڒ��܂ŕ�C���邷�ׂ�������Ȃ������̂ŁA�Ƃ肠������ڂ������Ă��镔���ɉ����Ăׂ��ׂ��h���Ă݂܂����B���̂Ƃ�������Ă������ł��B
�ڒ��܂������Ď��͂̂��̂Ƃ����ꍇ���悤�ɂȂ�ƁA�ڒ��܂�h�����Ƃ��낪���݂�ттĂ��܂����B�����C�ɔ��̔��_�݂͂��Ƃ��Ȃ��̂ŁA����͌C�n��h���č������悤�Ǝv���A�C�n���Ă���Ƃ����T�����̂ł����A�ӊO�Ƌߏ��ɔ����Ă���X�������̂ł��B
���������Ȃ��̂Ńl�b�g�ŒT���̂ł����A�C�n���A�}�]���ŒT���悤�ɂȂ�Ƃ͎v�������܂���ł����B
posted by �p�v���J2020 at 03:00| �i�J�e�S���Ȃ��j
2020�N11��14��
�Q�[���̐��E�Ő퍑�鏄��
�g�p���ꂽ�Q�[���́u�M���̖�]�v�ł��B
https://youtu.be/e3dIcAN2bIo
�Q�X�g�́u��s���C�^�[�̔�������v�u���j�i�r�Q�[�^�[�̂ꂫ���N���v�ł��B
�M���̖�]�Ƃ����Q�[���͒��L���ł����A���O�������������Ƃ�����܂���ł����B
�����A���jif���y���߂�Q�[���Ƃ����̂ł��傤�ˁB
���̔�������Ƃꂫ���N�����M���̖�]�ɏo�Ă���퍑�̏�������āA�y�������b������Ƃ������Ȃ̂ł��傤���A��ЂƂɂӂ���Ƃ��������������āA�O�i�߂Ȃ��̂����Ă��܂��܂��B
�M���̖�]�ɏo�Ă���n�`�́A�����̂��̂���ɗǂ��Č����Ă���炵���A��l�Ƃ��勻���ł��B
�ꂫ���N���̂���c�͂̂ڂ��̏�ŕ���ɂȂ����E��ŐΓc�����Ɛ���������ŁA���ݐΓc�O�������̂ꂫ���N���͐�c�Ɋ�������ł��Ȃ��Ə��Ă��܂����B
��������ĐM���̖�]�̃Q�[������肽���Ȃ������Ƃ����Ƙb�͕ʂŁA�n�}�肻���ȃQ�[���ɂ͋߂Â��܂���B
���ɂ�肽�����Ƃ�����̂ɂł��Ȃ��Ȃ��Ă��܂�����ł��B
https://youtu.be/e3dIcAN2bIo
�Q�X�g�́u��s���C�^�[�̔�������v�u���j�i�r�Q�[�^�[�̂ꂫ���N���v�ł��B
�M���̖�]�Ƃ����Q�[���͒��L���ł����A���O�������������Ƃ�����܂���ł����B
�����A���jif���y���߂�Q�[���Ƃ����̂ł��傤�ˁB
���̔�������Ƃꂫ���N�����M���̖�]�ɏo�Ă���퍑�̏�������āA�y�������b������Ƃ������Ȃ̂ł��傤���A��ЂƂɂӂ���Ƃ��������������āA�O�i�߂Ȃ��̂����Ă��܂��܂��B
�M���̖�]�ɏo�Ă���n�`�́A�����̂��̂���ɗǂ��Č����Ă���炵���A��l�Ƃ��勻���ł��B
�ꂫ���N���̂���c�͂̂ڂ��̏�ŕ���ɂȂ����E��ŐΓc�����Ɛ���������ŁA���ݐΓc�O�������̂ꂫ���N���͐�c�Ɋ�������ł��Ȃ��Ə��Ă��܂����B
��������ĐM���̖�]�̃Q�[������肽���Ȃ������Ƃ����Ƙb�͕ʂŁA�n�}�肻���ȃQ�[���ɂ͋߂Â��܂���B
���ɂ�肽�����Ƃ�����̂ɂł��Ȃ��Ȃ��Ă��܂�����ł��B

posted by �p�v���J2020 at 03:00| �i�J�e�S���Ȃ��j
2020�N11��13��
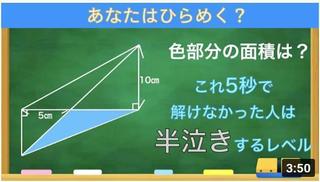
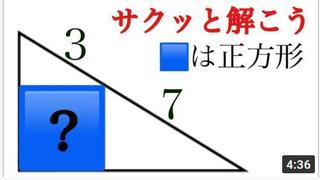
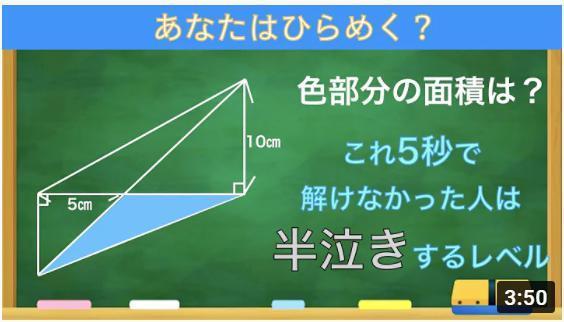
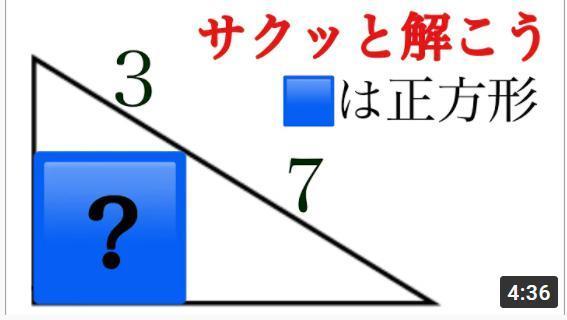
������

���C�Ɍ������Z�������Ɏ肱�����Ă��܂��B
YOUTUBE�ł͉�����悪����܂����A���Ȃ��ʼn��������A�Ƃ����~�]�ɕ����Ă���4�`5������ꓬ���Ă��܂��B
���Z������肾����ϕ��g������_�������A�~�̕������Ƃ��A�����Ƃ̌�_�Ƃ��܂ł͌v�Z���Ă����̂��ȁH����ł������Ȃ��̂ł��B
�������ɒ����Ƃ����Ă��܂����A���w���̐}�`�̒m���͈̔͂̃n�Y�ł��B
�厖�Ȍ����Ƃ��藝�Ƃ��Y��Ă���̂��A�⏕�������Έꔭ�ʼn����Ȃ̂��H
�⏕��������̂���ςȂ̂ł���ˁB
���ݕ������ł��B�������瑱���܂��B
posted by �p�v���J2020 at 03:00| �i�J�e�S���Ȃ��j
2020�N11��12��
���������ĕ�����
���������ĕ�������`�A�����������Ă邩������Ȃ���`�E�E�Ƃ����b�ł͂���܂���B
���H�̕\�ʂ���`���������ƂȂǖ�����������܂��A��`�����Ă݂�ƁA�ׂ����͗l�X�ł����l�X�ȑ傫����`�̗��ŕ����Ă��邱�ƂɋC���t���܂��B


���̂悤�ȉ摜�������_���͗l�Ƃ��e�N�X�`���͗l�Ƃ������܂��B�A�i���O�e���r�̎���A�������Ԃ��I������ƃX�s�[�J�[����U�[�Ƃ����G���ƂƂ��Ƀu���E���Ǐ�ɂ͍����̂悤�ȉ摜�������܂����B�܂��Ƀ����_���͗l�ł����B�i���ł̓f�W�^�������ɂȂ�A�������邱�Ƃ��ł��Ȃ��Ȃ�܂������j
���̃����_���͗l�͉��̓����������Ȃ��̂ŁA�������H�̏������ꂽ�Ƃ���̉摜���B���Ă��āA2���̉摜������ׂĂ݂��Ƃ��A�قƂ�nj����������Ȃ��ł��傤�B
�Ƃ��낪�A������@�i�Z�p�j�Ŕ�r����ƁA�����2�̉摜�͖��炩�ɕʕ����ƕ������Ă��܂��̂ł��B�����ł��ˁ`�B
���̕��@�i�Z�p�j�͉��̖��ɗ��̂��H�Ǝv���ł��傤���A�w��F�Ƃ���F�Ƃ��Ɏg��ꂽ�肵�Ă��܂���B
���H�̕\�ʂ���`���������ƂȂǖ�����������܂��A��`�����Ă݂�ƁA�ׂ����͗l�X�ł����l�X�ȑ傫����`�̗��ŕ����Ă��邱�ƂɋC���t���܂��B


���̂悤�ȉ摜�������_���͗l�Ƃ��e�N�X�`���͗l�Ƃ������܂��B�A�i���O�e���r�̎���A�������Ԃ��I������ƃX�s�[�J�[����U�[�Ƃ����G���ƂƂ��Ƀu���E���Ǐ�ɂ͍����̂悤�ȉ摜�������܂����B�܂��Ƀ����_���͗l�ł����B�i���ł̓f�W�^�������ɂȂ�A�������邱�Ƃ��ł��Ȃ��Ȃ�܂������j
���̃����_���͗l�͉��̓����������Ȃ��̂ŁA�������H�̏������ꂽ�Ƃ���̉摜���B���Ă��āA2���̉摜������ׂĂ݂��Ƃ��A�قƂ�nj����������Ȃ��ł��傤�B
�Ƃ��낪�A������@�i�Z�p�j�Ŕ�r����ƁA�����2�̉摜�͖��炩�ɕʕ����ƕ������Ă��܂��̂ł��B�����ł��ˁ`�B
���̕��@�i�Z�p�j�͉��̖��ɗ��̂��H�Ǝv���ł��傤���A�w��F�Ƃ���F�Ƃ��Ɏg��ꂽ�肵�Ă��܂���B

posted by �p�v���J2020 at 03:00| �i�J�e�S���Ȃ��j
2020�N11��11��
�����`
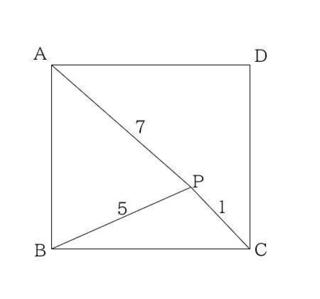
�����`ABCD�̓����̓_p������B
AP���V�ABP���T�ACP���P�̂Ƃ�
�����`�̖ʐς����߂�B
�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`
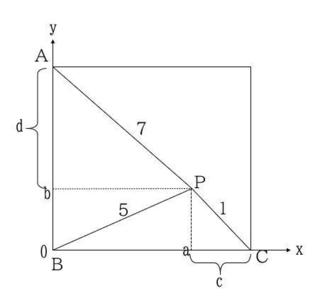
�}�̂悤�ɐ����`ABCD�̒��_B��xy���W��(0,0)�ɒu���B
P����x���ɐ��������낵x���Ƃ̌�_��(a,0)�A
������P����y���ɐ��������낵y���Ƃ̌�_��(0,b)�Ƃ���B
�_a���璸�_C�܂ł�c�A�_b���璸�_A�܂ł�d�Ƃ���B
��BaP�͒��p�O�p�`������A
�@a^2�{b^2��25�@�c�@�@
�ł���B
������
�@c��sqrt(1^2�|b^2)�@�c�@�A
�@d��sqrt�i7^2�|a^2)�@�c�@�B
�����`������AB��BC
����������
�@a�{sqrt(1^2�|b^2)��b�{sqrt�i7^2�|a^2)�@�c�@�C
�ڍ�����
�@a�|b��sqrt�i7^2�|a^2)�|sqrt(1^2�|b^2)
���ӂ��悷��
�@a^2�|2ab�{b^2���i7^2�|a^2)�{(1^2�|b^2)�|2sqrt(7^2�|a^2)sqrt(1^2�|b^2)
�@a^2�{b^2�|2ab��49�{1�|(a^2�{b^2)�|2sqrt(7^2�|a^2)sqrt(1^2�|b^2)
�@���
�@25�|2ab��50�|25�|2sqrt(7^2�|a^2)sqrt(1^2�|b^2)
�@ab��sqrt(7^2�|a^2)sqrt(1^2�|b^2)
����ɗ��ӂ��悷��
�@a^2b^2��(7^2�|a^2)(1^2�|b^2)
�@�@�@�@�@��49�|49b^2�|a^2�{a^2b^2
�@0��49�|48b^2�|(a^2�{b^2)
�@0��49�|25�|48b^2
�䂦��
�@48b^2��24
�@�@b^2��1/2
b�͐��Ȃ̂�
�@�@b��sqrt(2)/2
�@���
�@��^2��25�|1/2��49/2
a�����Ȃ̂�
�@a��7sqrt(2)/2
����Đ����`�̖ʐ�S��
�@S��(a�{sqrt(1^2�|b^2))^2
�@�@��(7sqrt(2)/2�{sqrt(2)/2)^2
�@�@��(4sqrt(2))^2
�@�@��16×2
�@�@��32
���@�����`�̖ʐς�32//
posted by �p�v���J2020 at 03:00| �i�J�e�S���Ȃ��j
2020�N11��10��
�召�W
���̂R�̎����`�A�a�A�b�̑召�W��s�����ŕ\���B
�`��100!�@�@�@�@�a��2^600�@�@�@�@�@�b��50^100
�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`
2�̙p��̌`���D���Ȃ̂ŁA�b��2�̙p��̌`�ɂ��܂��B
�b��(2×25)^100
�@�@��(2×32)^100
�@�@�@��(2×2^5)^100
�@�@�@��(2^6)^100
�@�@�@��2^600
�@�@�@���a
���b���a
���ɂ`�ł��B�`���Ȃ�Ƃ��p��̌`�ɂ����Ă����܂��B
�`��100!
�@��1×2×3×�E�E�E×100
�@��(50�|49)×(50�|48)×�E×50×�E�E×(50�{48)×(50�{49)×100
�@��(50�|1)×(50�{1�j×(50�|2)×(50�{2)×�E�E�E×(50�|49)×(50�{49)×50×100
�@��(50^2�|1)×(50^2�|2^2)×�E�E�E×(50^2�|48^2)×(1×99)×50×(2×50�j
�@�@��(50^2�|1)×(50^2�|2^2)×�E�E�E×(50^2�|48^2)×(100)×50×(2×50�j
�@�@�@��(50^2�|1)×(50^2�|2^2)×�E�E�E×(50^2�|48^2)×(2×50)×50×(2×50)
�@�@�@��(50^2�|1)×(50^2�|2^2)×�E�E�E×(50^2�|48^2)×50×50×50×4
�@�@�@�@��50^2�@�@×50^2�@ �@×�E�E�E ×50^2�@�@�@ ×50×50×50×50
�@�@�@�@�@��50^96×50×50×50×50
�@�@�@�@�@��50^100
�@�@�@�@�@���b
���`���b
���������ā@�`���b���a�@�y100! �� 50^100 �� 2^600�z//

�y���܂��z
p��p��5�̑f���B
p^3��p�|4�Ŋ������Ƃ��̗]�肪4�̂Ƃ��Ap�̒l�́H
�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`
p^3��p�|4�Ŋ����Ă݂܂��B
p^3/(p�|4)��(p^2�{4p�{16)�{64/(p�|4)
64/(p�|4)�ɒ��ڂ��܂��B
�����̊���Z��4�]��K�v������܂��B
����������60/(p�|4)�������Ȃ���Ȃ�܂���B
�܂��A�]�肪4�ł�����p�|4��5�ȏ�łȂ���Ȃ�܂���B
60��5�ȏ�̖́A5�A6�A10�A12�A15�A20�A30�A60�ł��B
����������p�|4��5�A6�A10�A12�A15�A20�A30�A60
�䂦��p��9�A10�A14�A16�A19�A24�A34�A64�ɂȂ�܂��B
�Ƃ���ő�ӂ���p��p��5�̑f���Ȃ̂ŁAp��19//
�y���Z�z
p^3��19×19×19��361×19��6859�A�����p�|4�ł���15�Ŋ����
6859÷15��457�E�E�E4//
�`��100!�@�@�@�@�a��2^600�@�@�@�@�@�b��50^100
�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`
2�̙p��̌`���D���Ȃ̂ŁA�b��2�̙p��̌`�ɂ��܂��B
�b��(2×25)^100
�@�@��(2×32)^100
�@�@�@��(2×2^5)^100
�@�@�@��(2^6)^100
�@�@�@��2^600
�@�@�@���a
���b���a
���ɂ`�ł��B�`���Ȃ�Ƃ��p��̌`�ɂ����Ă����܂��B
�`��100!
�@��1×2×3×�E�E�E×100
�@��(50�|49)×(50�|48)×�E×50×�E�E×(50�{48)×(50�{49)×100
�@��(50�|1)×(50�{1�j×(50�|2)×(50�{2)×�E�E�E×(50�|49)×(50�{49)×50×100
�@��(50^2�|1)×(50^2�|2^2)×�E�E�E×(50^2�|48^2)×(1×99)×50×(2×50�j
�@�@��(50^2�|1)×(50^2�|2^2)×�E�E�E×(50^2�|48^2)×(100)×50×(2×50�j
�@�@�@��(50^2�|1)×(50^2�|2^2)×�E�E�E×(50^2�|48^2)×(2×50)×50×(2×50)
�@�@�@��(50^2�|1)×(50^2�|2^2)×�E�E�E×(50^2�|48^2)×50×50×50×4
�@�@�@�@��50^2�@�@×50^2�@ �@×�E�E�E ×50^2�@�@�@ ×50×50×50×50
�@�@�@�@�@��50^96×50×50×50×50
�@�@�@�@�@��50^100
�@�@�@�@�@���b
���`���b
���������ā@�`���b���a�@�y100! �� 50^100 �� 2^600�z//

�y���܂��z
p��p��5�̑f���B
p^3��p�|4�Ŋ������Ƃ��̗]�肪4�̂Ƃ��Ap�̒l�́H
�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`
p^3��p�|4�Ŋ����Ă݂܂��B
p^3/(p�|4)��(p^2�{4p�{16)�{64/(p�|4)
64/(p�|4)�ɒ��ڂ��܂��B
�����̊���Z��4�]��K�v������܂��B
����������60/(p�|4)�������Ȃ���Ȃ�܂���B
�܂��A�]�肪4�ł�����p�|4��5�ȏ�łȂ���Ȃ�܂���B
60��5�ȏ�̖́A5�A6�A10�A12�A15�A20�A30�A60�ł��B
����������p�|4��5�A6�A10�A12�A15�A20�A30�A60
�䂦��p��9�A10�A14�A16�A19�A24�A34�A64�ɂȂ�܂��B
�Ƃ���ő�ӂ���p��p��5�̑f���Ȃ̂ŁAp��19//
�y���Z�z
p^3��19×19×19��361×19��6859�A�����p�|4�ł���15�Ŋ����
6859÷15��457�E�E�E4//
posted by �p�v���J2020 at 03:00| �i�J�e�S���Ȃ��j