2020年11月17日
高校入試問題(数学1問)が解けました
奮闘中の問題がようやく解けました。

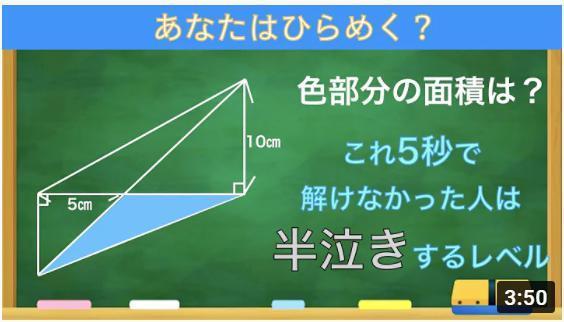
奮闘していたのは下図の問題でした。
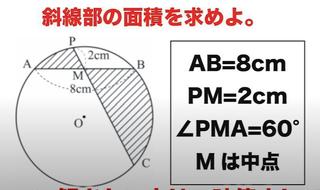
まず、中学数学は何処までか、を見極めます。
円周角と中心角の関係はOK。三平方の定理はOK。特別な三角形(直角、60°、30°)及び三角形(直角、45°、45°)の辺の比はOK。図形の相似はOK。円周率はπはOK。ということで、計算を始めます。
図中の長さの単位はcmですが、以下では単位を外して説明していきます。
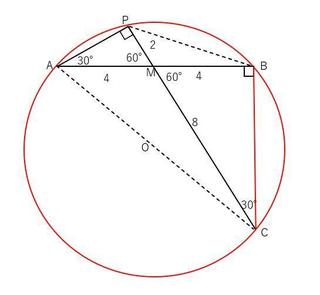
⊿AMPにおいて、2辺に挟まれた角が60°で、辺の比が1:2であることに気付きます。
これは、∠60°、∠30°、∠90°の角度をもつ直角三角形です。したがって、斜辺APは2sqrt(3)と計算できます。
弧ACの円周角である∠APCが直角なので、線分ACはこの円の直径になります。
また∠ABCも弧ACの円周角なので直角になります。
次に、∠AMP=∠CMB=60°であり、∠APM=∠CBM=90°なので、⊿AMP∽⊿CMBでその比は1:2です。したがって、辺BC=4sqrt(3)です。
直角⊿ABCにおいて三平方の定理より、円の直径ACが求まります。
AC=sqrt(8^2+4^2×3)=4sqrt(7)です。
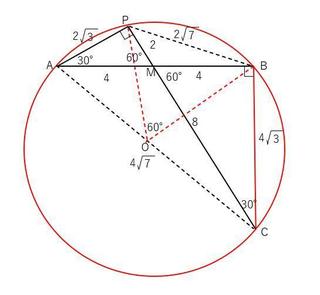
弧PBの円周角∠PAB=30°なので、中心角は60°になります。
したがって⊿POBは一辺の長さが円の半径に等しい長さの正三角形です。
扇形POBの面積は円の面積の1/6になります。
扇形POBの面積=(2sqrt(7))^2×π/6=28π/6=(14/3)π
正三角形POBの面積=2sqrt(7)×sqrt(21)/2=7sqrt(3)
よって、弧PBと線分PBで囲まれた部分の面積S1=(14/3)π-7sqrt(3)
次に、⊿PMBの面積=⊿AMPの面積=S2(底辺が4で等しく、かつ高さが同じ)
ゆえに、S2=2×2sqrt(3)/2=2sqrt(3)
また、⊿AMCの面積=⊿CMBの面積=S3(底辺が4で等しく、かつ高さが同じ)
ゆえに、S3=4×4sqrt(3)/2=8sqrt(3)
したがって求める面積は、
半円の面積から、S1+S2+S3を引けば求まります。
半円の面積=14πなので、求める面積をSとするとS=14π-(S1+S2+S3)です。
それぞれに数値を代入すると
S=14π-((14/3)π-7sqrt(3)+2sqrt(3)+8sqrt(3))
=(28/3)π-3sqrt(3)
単位を戻すと求める面積は
( (28/3)π-3sqrt(3) ) cm^2
となります。
メデタシめでたし
~~~~~~~~~~~~~~~~~~~~~~~
次も高校入試問題で奮闘中です。

とっかかりを探しています。
4^24 < 5^24 < 6^24 < 8^24
(2^2)^24=2^48 → 2^48 < 5^24
8^24=(2^3)^24=2^72 → 5^24 < 2^72
奮闘中です。

奮闘していたのは下図の問題でした。

まず、中学数学は何処までか、を見極めます。
円周角と中心角の関係はOK。三平方の定理はOK。特別な三角形(直角、60°、30°)及び三角形(直角、45°、45°)の辺の比はOK。図形の相似はOK。円周率はπはOK。ということで、計算を始めます。
図中の長さの単位はcmですが、以下では単位を外して説明していきます。

⊿AMPにおいて、2辺に挟まれた角が60°で、辺の比が1:2であることに気付きます。
これは、∠60°、∠30°、∠90°の角度をもつ直角三角形です。したがって、斜辺APは2sqrt(3)と計算できます。
弧ACの円周角である∠APCが直角なので、線分ACはこの円の直径になります。
また∠ABCも弧ACの円周角なので直角になります。

次に、∠AMP=∠CMB=60°であり、∠APM=∠CBM=90°なので、⊿AMP∽⊿CMBでその比は1:2です。したがって、辺BC=4sqrt(3)です。
直角⊿ABCにおいて三平方の定理より、円の直径ACが求まります。
AC=sqrt(8^2+4^2×3)=4sqrt(7)です。
弧PBの円周角∠PAB=30°なので、中心角は60°になります。
したがって⊿POBは一辺の長さが円の半径に等しい長さの正三角形です。
扇形POBの面積は円の面積の1/6になります。
扇形POBの面積=(2sqrt(7))^2×π/6=28π/6=(14/3)π
正三角形POBの面積=2sqrt(7)×sqrt(21)/2=7sqrt(3)
よって、弧PBと線分PBで囲まれた部分の面積S1=(14/3)π-7sqrt(3)
次に、⊿PMBの面積=⊿AMPの面積=S2(底辺が4で等しく、かつ高さが同じ)
ゆえに、S2=2×2sqrt(3)/2=2sqrt(3)
また、⊿AMCの面積=⊿CMBの面積=S3(底辺が4で等しく、かつ高さが同じ)
ゆえに、S3=4×4sqrt(3)/2=8sqrt(3)
したがって求める面積は、
半円の面積から、S1+S2+S3を引けば求まります。
半円の面積=14πなので、求める面積をSとするとS=14π-(S1+S2+S3)です。
それぞれに数値を代入すると
S=14π-((14/3)π-7sqrt(3)+2sqrt(3)+8sqrt(3))
=(28/3)π-3sqrt(3)
単位を戻すと求める面積は
( (28/3)π-3sqrt(3) ) cm^2
となります。
メデタシめでたし
~~~~~~~~~~~~~~~~~~~~~~~
次も高校入試問題で奮闘中です。

とっかかりを探しています。
4^24 < 5^24 < 6^24 < 8^24
(2^2)^24=2^48 → 2^48 < 5^24
8^24=(2^3)^24=2^72 → 5^24 < 2^72
奮闘中です。
【このカテゴリーの最新記事】
-
no image