2022年02月09日
正方形の面積を求める
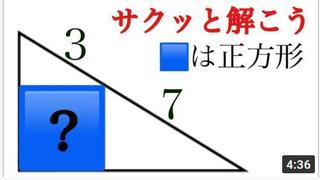
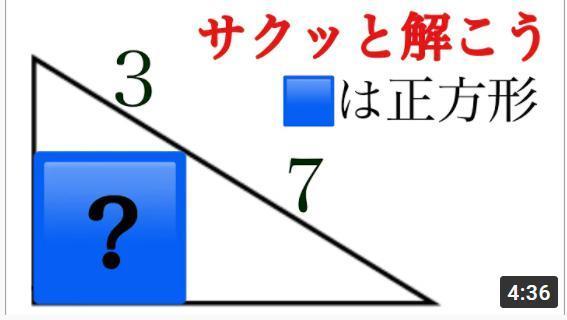
Q:青色で塗りつぶされた正方形の面積を求めよ。
A:
正方形の一辺の長さをxとする。
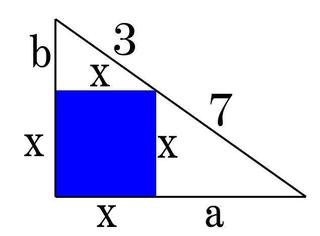
斜辺が3、7、10(=3+7)の直角三角形は全て相似形。
よって3:x=7:a
∴7*x=3*a
したがって
a=(7/3)*x
また、7:x=3:b
∴3*x=7*b
したがって
b=(3/7)*x
以上より
x+b=x+(3/7)*x=(10/7)*x
x+a=x+(7/3)*x=(10/3)*x
与えられた直角三角形の各辺の比は
10:(10/7)*x:(10/3)*x
=1:(x/7):(x/3)
=21:3*x:7*x
よって三平方の定理を用いて
9*x^2+49*x^2=21^2
(9+49)*x^2=441
x^2=441/58
正方形の一辺の長さがxだったので
正方形の面積は 441/58
【このカテゴリーの最新記事】
-
no image