パプリカ2020の部屋

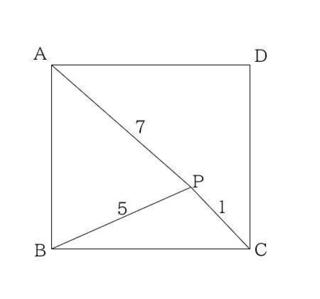
正方形ABCDの内部の点pがある。
AP＝７、BP＝５、CP＝１のとき
正方形の面積を求めよ。
〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜


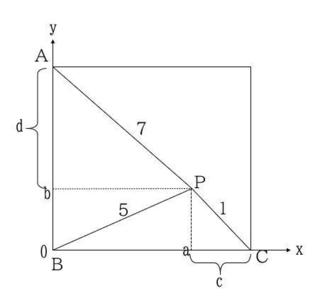
図のように正方形ABCDの頂点Bをxy座標の(0,0)に置く。
Pからx軸に垂線を下ろしx軸との交点を(a,0)、
同じくPからy軸に垂線を下ろしy軸との交点を(0,b)とする。
点aから頂点Cまでをc、点bから頂点Aまでをdとする。

�傳aPは直角三角形だから、
　a^2＋b^2＝25　…　�@
である。

ここで
　c＝sqrt(1^2−b^2)　…　�A
　d＝sqrt（7^2−a^2)　…　�B

正方形だからAB＝BC
したがって
　a＋sqrt(1^2−b^2)＝b＋sqrt（7^2−a^2)　…　�C
移項して
　a−b＝sqrt（7^2−a^2)−sqrt(1^2−b^2)
両辺を二乗する
　a^2−2ab＋b^2＝（7^2−a^2)＋(1^2−b^2)−2sqrt(7^2−a^2)sqrt(1^2−b^2)
　a^2＋b^2−2ab＝49＋1−(a^2＋b^2)−2sqrt(7^2−a^2)sqrt(1^2−b^2)
�@より
　25−2ab＝50−25−2sqrt(7^2−a^2)sqrt(1^2−b^2)
　ab＝sqrt(7^2−a^2)sqrt(1^2−b^2)
さらに両辺を二乗する
　a^2b^2＝(7^2−a^2)(1^2−b^2)
　　　　　＝49−49b^2−a^2＋a^2b^2
　0＝49−48b^2−(a^2＋b^2)
　0＝49−25−48b^2
ゆえに
　48b^2＝24
　　b^2＝1/2
bは正なので
　　b＝sqrt(2)/2

�@より
　ａ^2＝25−1/2＝49/2
aも正なので
　a＝7sqrt(2)/2

よって正方形の面積Sは
　S＝(a＋sqrt(1^2−b^2))^2
　　＝(7sqrt(2)/2＋sqrt(2)/2)^2
　　＝(4sqrt(2))^2
　　＝16×2
　　＝32

∴　正方形の面積は32//