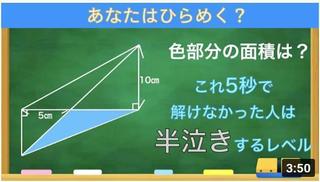
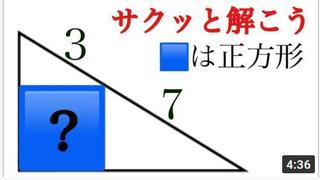
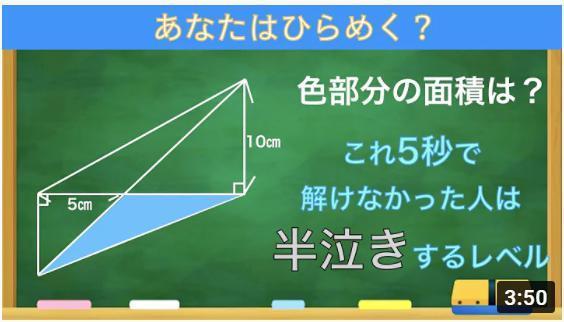
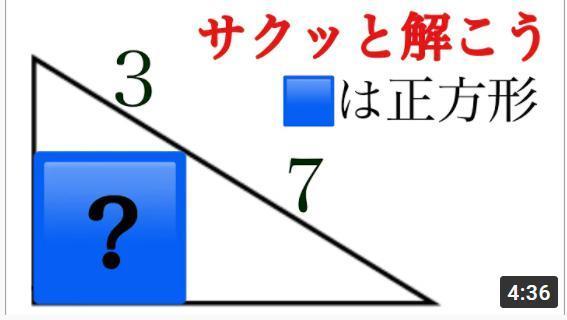
�V�K�L���̓��e���s�����ƂŁA��\���ɂ��邱�Ƃ��\�ł��B
�L��
�V�K�L���̓��e���s�����ƂŁA��\���ɂ��邱�Ƃ��\�ł��B
posted by fanblog
2020�N11��29��
���Ƃ�
�������ł���؋��Ƃ́H
���ł���Ƃ����ӎ��B���Ƃ��Ă̘A�������L���B�A�������L���ɂ��鎄�̐g�̂Ɠ����`��̐g�̂̕ێ��B
�������ł���ƔF���ł���̂́A�`�͎��Ă��邪���ƈႤ���҂Ƌ�ʏo����Ƃ������Ƃ��Ǝv���܂��B
�A�������L���͎������ԂƂ�������̒��ň�ѐ���ۂ��Ă���Ƃ������Ƃł͂Ȃ��ł��傤���B
�A�������L���ɂ��鎄�̐g�̂Ɠ����`��̕ێ��Ƃ́A����̎��ƍ����̎�������������ē����g�̓I�����������Ă���Ɗm�F�ł��邱�Ƃł͂Ȃ����ƁB
�l�Ԃ������E�ł������ЂƂ肵�����Ȃ���Ύ����l�Ԃ��Ƃ����ӎ��⎄�͑��҂Ƃ͈Ⴄ�Ƃ����ӎ��͐��܂�悤���Ȃ��Ǝv���̂ł��B
�A�������L���̒�`�͞B���ł��ˁB�A���t����ꂽ�L���Ƃ������̂����肷��ƁA�L���̘A�����ɂ͈Ӗ����Ȃ��Ȃ�悤�ȋC�����܂��B
�Ⴆ�A�݂�Ȃ��D���ȏ��N�W�����v�̘A�ڃ}���K��1�b�̏�ʂŕ��ꂪ�n�܂�Ƃ��A�o��l�������͂��̐��ɍ�҂ɂ���Ă͂��߂đn�����ꂽ�̂ɁA���łɎp�`�͊������Ă���A�A�������L���������Ă��܂��B��҂��n����ƂȂ�A�������̂Ƃ����N�W�����v�ɘA�ڂ��n�߂��}���K�̐��E���������ꂽ�p�őn�������ƌ��邱�Ƃ��ł��Ă��܂��̂ł��B
����ƍ����̐g�̂�����Ƃ���̂��^�킵���ł��B
�������̐g�͓̂��X�X�N���b�v���r���h���s���Ă���A�ق�1�N���ĂΕ����I�ɂ͓���ւ���Ă��܂��Ă��܂��B�܂��A��Â��i�݁A�g�̂̈ꕔ�܂��͑S�����l�H���Œu������������A����̐g�̂Ƃ̓��ꐫ�͌����Ȃ��Ȃ�̂ł́B
���܂�[�݂ɂ͂͂܂肽���Ȃ��̂ł����A�u���͒N�H�����͉����H�v�ƂƂڂ��Ȃ��Łu���͒N���A�����͉������v�Ǝ��Ȃ����߂Ȃ������Ԃ����̂����܂ɂ͗L���ƍl����̂ł��B

���ł���Ƃ����ӎ��B���Ƃ��Ă̘A�������L���B�A�������L���ɂ��鎄�̐g�̂Ɠ����`��̐g�̂̕ێ��B
�������ł���ƔF���ł���̂́A�`�͎��Ă��邪���ƈႤ���҂Ƌ�ʏo����Ƃ������Ƃ��Ǝv���܂��B
�A�������L���͎������ԂƂ�������̒��ň�ѐ���ۂ��Ă���Ƃ������Ƃł͂Ȃ��ł��傤���B
�A�������L���ɂ��鎄�̐g�̂Ɠ����`��̕ێ��Ƃ́A����̎��ƍ����̎�������������ē����g�̓I�����������Ă���Ɗm�F�ł��邱�Ƃł͂Ȃ����ƁB
�l�Ԃ������E�ł������ЂƂ肵�����Ȃ���Ύ����l�Ԃ��Ƃ����ӎ��⎄�͑��҂Ƃ͈Ⴄ�Ƃ����ӎ��͐��܂�悤���Ȃ��Ǝv���̂ł��B
�A�������L���̒�`�͞B���ł��ˁB�A���t����ꂽ�L���Ƃ������̂����肷��ƁA�L���̘A�����ɂ͈Ӗ����Ȃ��Ȃ�悤�ȋC�����܂��B
�Ⴆ�A�݂�Ȃ��D���ȏ��N�W�����v�̘A�ڃ}���K��1�b�̏�ʂŕ��ꂪ�n�܂�Ƃ��A�o��l�������͂��̐��ɍ�҂ɂ���Ă͂��߂đn�����ꂽ�̂ɁA���łɎp�`�͊������Ă���A�A�������L���������Ă��܂��B��҂��n����ƂȂ�A�������̂Ƃ����N�W�����v�ɘA�ڂ��n�߂��}���K�̐��E���������ꂽ�p�őn�������ƌ��邱�Ƃ��ł��Ă��܂��̂ł��B
����ƍ����̐g�̂�����Ƃ���̂��^�킵���ł��B
�������̐g�͓̂��X�X�N���b�v���r���h���s���Ă���A�ق�1�N���ĂΕ����I�ɂ͓���ւ���Ă��܂��Ă��܂��B�܂��A��Â��i�݁A�g�̂̈ꕔ�܂��͑S�����l�H���Œu������������A����̐g�̂Ƃ̓��ꐫ�͌����Ȃ��Ȃ�̂ł́B
���܂�[�݂ɂ͂͂܂肽���Ȃ��̂ł����A�u���͒N�H�����͉����H�v�ƂƂڂ��Ȃ��Łu���͒N���A�����͉������v�Ǝ��Ȃ����߂Ȃ������Ԃ����̂����܂ɂ͗L���ƍl����̂ł��B

�y���̃J�e�S���[�̍ŐV�L���z
-
no image
posted by �p�v���J2020 at 03:00| �i�J�e�S���Ȃ��j
2020�N11��28��
�X���\
�X���܂�����̂ŕX�Z�[�������Ă���O���A���e�B�[�N�Ƌ�̂��X������܂����B�����������Ă����̗ނ̉Ƌ�͔���Ȃ����낤�ȂƎv���Ȃ���X�̑O��ʂ�߂��܂����B
�b������ƌ��̓X�͕X�Z�[���̊Ŕ�Еt���Ēʏ�c�Ƃ����Ă��܂����B�X�̌o�c�������������̂��ȁA�Ǝv���Ȃ���X�̑O��ʂ�߂��܂����B���ς�炸�����Ƃ͎�̍���Ȃ��Ƌ�u���Ă���Ȃ��A�Ǝv���܂����B
�Y�ꂽ���A�X�Z�[���n�߂܂����B�����Ă��炭����Ƃ܂��ʏ�c�Ƃɖ߂�܂����B
���̌��i��3�x�ڂɌ��������Ƃ��A���̓X�͒���I�ɕX�Z�[�������Ă���X���ƕ�����܂����B
�m���Ɂu�X�v�Ƃ��u����v�Ƃ��u�c�肠�Ƌ͂��v�Ƃ�������ƁA�������S�����������܂��B
�������A�{���ɓX���܂�������Ȃ�u��͍���Ȃ��������ǁA�Ȃ��Ȃ�ƂȂ�ƂȂ��₵���v�ȂǂƎv���̂ł����A��K�I�ɂ��̎�@���g���ƉR���ȓX�ɂȂ��Ă��܂��܂��B
�����I�ɂ͕X���\�ƌĂ�ł��܂��B
�����Ă������̂͑S���{���������̂ł��傤���A�ʂ̈Ӗ��œX�̐M�p�͂Ȃ��Ȃ��Ă����̂ł͂Ȃ��̂��Ǝv���܂��B

�b������ƌ��̓X�͕X�Z�[���̊Ŕ�Еt���Ēʏ�c�Ƃ����Ă��܂����B�X�̌o�c�������������̂��ȁA�Ǝv���Ȃ���X�̑O��ʂ�߂��܂����B���ς�炸�����Ƃ͎�̍���Ȃ��Ƌ�u���Ă���Ȃ��A�Ǝv���܂����B
�Y�ꂽ���A�X�Z�[���n�߂܂����B�����Ă��炭����Ƃ܂��ʏ�c�Ƃɖ߂�܂����B
���̌��i��3�x�ڂɌ��������Ƃ��A���̓X�͒���I�ɕX�Z�[�������Ă���X���ƕ�����܂����B
�m���Ɂu�X�v�Ƃ��u����v�Ƃ��u�c�肠�Ƌ͂��v�Ƃ�������ƁA�������S�����������܂��B
�������A�{���ɓX���܂�������Ȃ�u��͍���Ȃ��������ǁA�Ȃ��Ȃ�ƂȂ�ƂȂ��₵���v�ȂǂƎv���̂ł����A��K�I�ɂ��̎�@���g���ƉR���ȓX�ɂȂ��Ă��܂��܂��B
�����I�ɂ͕X���\�ƌĂ�ł��܂��B
�����Ă������̂͑S���{���������̂ł��傤���A�ʂ̈Ӗ��œX�̐M�p�͂Ȃ��Ȃ��Ă����̂ł͂Ȃ��̂��Ǝv���܂��B

posted by �p�v���J2020 at 03:00| �i�J�e�S���Ȃ��j
2020�N11��27��
�S�W��
�S�W���͐��������ʼni�����肩��ڊo�߂��Ñ㐶���ł��̂��炾�͕��˔\�̂��ߕϗe���Ă��܂��Ă���Ƃ����z��ł��B
�ǂ̂��炢�Ñォ�͉f��̒��̔��m������Ă��܂����u100���N�O�v�Ƃ������Ƃł��B
�S�W�������삳�ꂽ����A�Ñ㐶���̋������������������100���N�O�Ƃ����F���������̂ł��傤���H
����Ƃ������Ƃ͕ʂ̐�����z�肵�Ă����̂ł��傤���B
����S�W���̖ڂ͔��ɕ|�������B���̌�̐l�ނ̖����ƂȂ�L���O�M�h���Ȃǂ̉F�����b�Ɠ����S�W���Ƃ͂܂������َ��̋��|�����������鋰�낵���ڂ����Ă��܂����B
����́A�f��قŌ����̂ł͂Ȃ��A�����^���r�f�I�Ō����̂ł��B�����Â̘b�ł�������Y�ꋎ���Ă��邩������܂��A�Đ��̃r�f�I�f�b�L�̓���VHS�̂ǂ��炩���e�������邩�̌������킢���J��Ђ낰���Ă�������ł��B�Ñ㐶���Ȃ�ʎ�����H�̏�����J��L���Ă��܂����B
�ŏI�I�ɂ�VHS�����������̂ł����A����͈ڂ�ς��A���ł̓u���[���C�f�B�X�N�̎���ł���A���邢�̓l�b�g�ʼnf�挩����̎���ɂȂ�܂����B
�S�W���f��͎�����o�čĂѕ|���S�W���ɂȂ����悤�ł��B

�ǂ̂��炢�Ñォ�͉f��̒��̔��m������Ă��܂����u100���N�O�v�Ƃ������Ƃł��B
�S�W�������삳�ꂽ����A�Ñ㐶���̋������������������100���N�O�Ƃ����F���������̂ł��傤���H
����Ƃ������Ƃ͕ʂ̐�����z�肵�Ă����̂ł��傤���B
����S�W���̖ڂ͔��ɕ|�������B���̌�̐l�ނ̖����ƂȂ�L���O�M�h���Ȃǂ̉F�����b�Ɠ����S�W���Ƃ͂܂������َ��̋��|�����������鋰�낵���ڂ����Ă��܂����B
����́A�f��قŌ����̂ł͂Ȃ��A�����^���r�f�I�Ō����̂ł��B�����Â̘b�ł�������Y�ꋎ���Ă��邩������܂��A�Đ��̃r�f�I�f�b�L�̓���VHS�̂ǂ��炩���e�������邩�̌������킢���J��Ђ낰���Ă�������ł��B�Ñ㐶���Ȃ�ʎ�����H�̏�����J��L���Ă��܂����B
�ŏI�I�ɂ�VHS�����������̂ł����A����͈ڂ�ς��A���ł̓u���[���C�f�B�X�N�̎���ł���A���邢�̓l�b�g�ʼnf�挩����̎���ɂȂ�܂����B
�S�W���f��͎�����o�čĂѕ|���S�W���ɂȂ����悤�ł��B

posted by �p�v���J2020 at 03:00| �i�J�e�S���Ȃ��j
2020�N11��26��
�\�N�g�J�Q
�����e�B���m�T�E���X�̂��Ƃł��B
�e�B���m�T�E���X�͍�����6800���N�O�`6700���N�O�ɑS�����ɂ߂��n��ŋ��̓��H�b�ƐM�����Ă��܂��B
��������͖�2���N�����܂������A���̒��ōŋ��������ł��B�ł�6700���N�O�ɋ����̎���͏I�����܂����B�V����͋���覐��������A�n��ł̓C���h�f�J�������̑啬�Ύ��オ�n�܂�������ł��B
�����͒N���������Ƃ͂���܂��A����覐��~���Ă����Ƃ�����������Ƃ͂���܂���B�C���h�̃f�J�������̑啬���m��܂���B�ł�����l������Ɖ��C�Ȃ��y��ɌÑ�̑����������Ă��܂��悤�ł��B
�����̖���͌��݂����݂ŁA���Ɏp��ς��Đ����c��܂����B���̒����e�B���m�T�E���X�̌n���̈�h���番���ꂽ�悤�ł��B
���̍\����A�Ɠ��̌ċz��n�́A�ٓ��ނ����D��Ă���悤�ɂ݂��܂��B�������łт��Ƃ��Ă��A��͂�ēx�n����x�z����̂͋����̒��Ԃ̂悤�ȋC������̂ł����A���n����x�z���Ă���̂͂ٓ��ނł��B
�����ٓ��ނ̌����������̂ł��傤���B

�e�B���m�T�E���X�͍�����6800���N�O�`6700���N�O�ɑS�����ɂ߂��n��ŋ��̓��H�b�ƐM�����Ă��܂��B
��������͖�2���N�����܂������A���̒��ōŋ��������ł��B�ł�6700���N�O�ɋ����̎���͏I�����܂����B�V����͋���覐��������A�n��ł̓C���h�f�J�������̑啬�Ύ��オ�n�܂�������ł��B
�����͒N���������Ƃ͂���܂��A����覐��~���Ă����Ƃ�����������Ƃ͂���܂���B�C���h�̃f�J�������̑啬���m��܂���B�ł�����l������Ɖ��C�Ȃ��y��ɌÑ�̑����������Ă��܂��悤�ł��B
�����̖���͌��݂����݂ŁA���Ɏp��ς��Đ����c��܂����B���̒����e�B���m�T�E���X�̌n���̈�h���番���ꂽ�悤�ł��B
���̍\����A�Ɠ��̌ċz��n�́A�ٓ��ނ����D��Ă���悤�ɂ݂��܂��B�������łт��Ƃ��Ă��A��͂�ēx�n����x�z����̂͋����̒��Ԃ̂悤�ȋC������̂ł����A���n����x�z���Ă���̂͂ٓ��ނł��B
�����ٓ��ނ̌����������̂ł��傤���B

posted by �p�v���J2020 at 03:00| �i�J�e�S���Ȃ��j
2020�N11��25��
���X���D��
����N�̓��L�ɂ���Ȏ��������Ă������Ƃ��܂��B
�u3��1���͓��j���ŏj���A����̓��ł����B�v
���邢�́A
�u�����̂������̓R���b�P�A������R���b�P�A�������R���b�P�A�����������R���b�P�A�����Ė�������R���b�P�A�E�E�E�v
������
�u���ނ̌����̗��v
�u���v�ɌW��Ƃ�����Ђ炪�Ȃɂ��Ă݂܂��ƁA
�ɂ����A�������A�ɂ��A�сA���A�ЁA
���ƂƂ��A���̂��A���傤�A�������A�������āA
�����ҁA
�ό����݂ȓǂݕ������܂��ˁB����I�Ɏg���Ă���̂ŋC�ɂ��Ă��܂���ł������A���炽�߂Č���ƕω����������܂��B
�q�ǂ��̍��͊o���邱�Ƃ���������ƕ���������Ă����ł��傤���A���ƂȂ��Ă͖��킢�[���ƚ����Ă����܂��B
���{����w�K����O���̕��͑�ςł��B�ł����̂������{�l��藬���Ɏg����悤�ɂȂ��Ă��܂���ł���B

�u3��1���͓��j���ŏj���A����̓��ł����B�v
���邢�́A
�u�����̂������̓R���b�P�A������R���b�P�A�������R���b�P�A�����������R���b�P�A�����Ė�������R���b�P�A�E�E�E�v
������
�u���ނ̌����̗��v
�u���v�ɌW��Ƃ�����Ђ炪�Ȃɂ��Ă݂܂��ƁA
�ɂ����A�������A�ɂ��A�сA���A�ЁA
���ƂƂ��A���̂��A���傤�A�������A�������āA
�����ҁA
�ό����݂ȓǂݕ������܂��ˁB����I�Ɏg���Ă���̂ŋC�ɂ��Ă��܂���ł������A���炽�߂Č���ƕω����������܂��B
�q�ǂ��̍��͊o���邱�Ƃ���������ƕ���������Ă����ł��傤���A���ƂȂ��Ă͖��킢�[���ƚ����Ă����܂��B
���{����w�K����O���̕��͑�ςł��B�ł����̂������{�l��藬���Ɏg����悤�ɂȂ��Ă��܂���ł���B

posted by �p�v���J2020 at 03:00| �i�J�e�S���Ȃ��j
2020�N11��24��
�߂�����
�ʂɗ�ɜ߂���Ă���킯�ł͂Ȃ��A�p��2�������ɜ߂���Ă���̂ł��B
�H�H�B������������Ă�́H
�߂���ꂽ���̂́�����ł��B
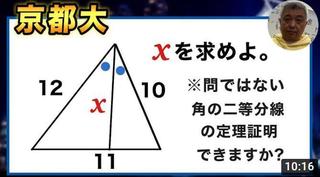
���͂���͍��Z���wA�̐}�`��I������Ƌ��ȏ��ɒ藝�̏ؖ����Ƃ��čڂ��Ă��邻���ł��B�����A�ӂ��͐�A�͑I�����Ȃ��炵���A�قƂ�ǂ̎��͖��m�̖��ƂȂ�킯�ł��B���������̎�ʼn����A�Ƃ������ƂȂ̂ł��B
�ؖ��͈ȉ��̂Ƃ���ł��B�������Ă��܂��Ύ��ɊȒP�ł��B
�����A�ؖ���܂�2�i�K�܂Ȃ��Ă͂Ȃ炸�A��1�i�K�ŕ��s���̕⏕���������A��2�i�K�ŎO�p�`�ɊO�ڂ���~�i������⏕���Ƃ����̂��H�j��`���K�v������܂��B
���p����O�ɁA���͋C�Â��̂��H�Ƃ����Ƃ���ł��傤���B
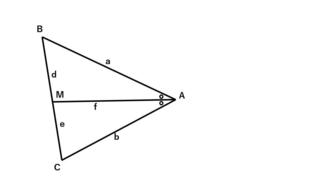
���̎O�p�`����ABC�Ƃ��A��A��2��������BC�̌�_��M�Ƃ��܂��B
�e�ӂ̒������AAB��a�AAC��b�AAM��f�ABM��d�AMC��e�Ƃ��܂��B�ic�͑啶����C�ƕ���킵���̂Ŏg�p���܂���B�j
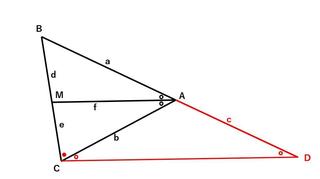
C��ʂ�MA�ɕ��s�Ȑ��ƁABA��A�̕����ɐL���������Ƃ̌�_��D�Ƃ��܂��B
���s��AM��CD������2����BC�y��BD�ɂ����āAd�Fe��a�Fc�����藧���܂��B
�܂�AM��CD�͕��s�Ȃ̂Ł�BAC����ADC�A���l�Ɂ�MAC��ACD�A
���Ƃ��Ɓ�BAC����MAC�i�p��2�����j�Ȃ̂ŁA��ADC����ACD�A
���������ć�ACD��2���ӎO�p�`�Ȃ̂ŁAc��b�ɂȂ�܂��B
d�Fe��a�Fb
a��12�Ab��10�Ad�{e��11����A
12e��10d�Ae��11�|d��������ƁA
12(11�|d)��10d�A132�|12d��10d�A22d��132�A
����������d��6�Ae��11�|6��5�A�ƂȂ�܂��B
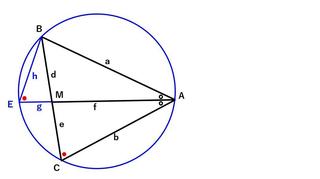
����
��ABC�̊O�ډ~��`���AAM�̉������Ɖ~���Ƃ̌�_��E�Ƃ��܂��B
EM��g�AEB��h�Ƃ��܂��B
��BEA����MCA�i�~���p�j�A��BAE��MAC�i�p��2�����j
���������ć�BEA�䇙AGC�ɂȂ�܂��B
������Aa�F(f�{g)��f�Fb
�܂��A��BME�䇙AMC�Ȃ̂ŁAg�Fe��d�Ff
���������āAf^2�{fg��ab��12×10��120
�܂��Afg��de��6×5��30
�����f^2�{30��120�Af^2��90�Af��3sqrt(10)��0�A
AM�̒������@3sqrt(10)�@�ł��B
�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`
���āA�߂���ꂽ�̂́A�����̕����ł͂Ȃ��āA
�u���Ⴀ�A���̒藝�ɋC�Â��Ȃ�������A���ɂǂ�ȕ��@�ʼn����̂��낤���H�v�Ƃ����^��������Ă��܂������Ƃł��B
��������I��肻�����Ȃ��v�Z���n�܂���������킯�Ȃ̂ł��B
�Ȃ�Ă��������I�I
�⏕����2�{�����܂����B
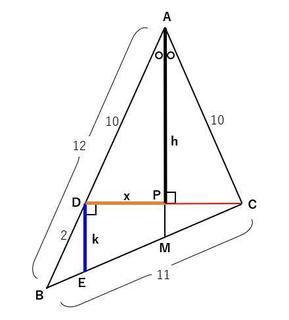
��ABC�ɂ����āA�_C�����A�̓����ɐ��������낵��_��P�Ƃ���B
���̐���������ɐL����AB�Ƃ̌�_��D�Ƃ���B
D����AM�ƕ��s�Ȑ�������BC�Ƃ̌�_��E�Ƃ���B
��ABM�䇙DBM�i��BAM����BDE�A��AMB��DEB�A��B�͋��ʁj
���������āA
12�F2��(BE�{EM)�FBE
�܂��A
EM��MC�A
BE�{EM�{MC��BE�{2EM��11
(BE�{EM)��6BE
EM��5BE
BE�{2×5BE��11BE��11
�䂦��BE��1�ABM��6�AMC��5
DE�FAM��2�F12��1�F6�Ȃ̂�
DE��������A�����6�{����悢�B
��ABC�̖ʐς�S�Ƃ���B
t���i10�{11�{12�j/2��33/2�Ƃ����Ƃ�
S��sqrt(t(t�|10)(t�|11)(t�|12))
�@��sqrt(33/2)(13/2)(11/2)(9/2))
�@���i1/4�jsqrt(3×11×13×11×3×3)
�@��(33/4)sqrt(39)
��ADC�̖ʐς�S1�Ƃ����
S1��S×(5/6)��(5/6)(33/4)sqrt(39)
�@�@��(55/8)sqrt(39)
�O�����̒藝����
x^2�{h^2��100
�܂�
xh��S1��(55/8)sqrt(39)
����������
x^2�{(1/x^2)(55×55×39/64)��100
x��0�Ȃ̂�
x^4�|100x^2�{(55×55×39/64)��0
x^2��X�Ƃ����ƁA
X^2�|100X^2�{(55×55×39/64)��0
���̂Ƃ�
X=195/8�A�@X=605/8
����������
x��(11/4)sqrt(10)��8.69����A�@x��(1/4)sqrt(390)��4.93���
5.5��x��0�Ȃ̂�
x��(1/4)sqrt(390)
��DBC�̖ʐ�S2��
S2��(1/6)S��(1/6)(33/4)sqrt(39)��(11/8)sqrt(39)
�����
��DEC�̖ʐ�S3��
S3��(10/11)(11/8)sqrt(39)��(5/4)sqrt(39)
����������
2xk(1/2)��xk��(5/4)sqrt(39)
k��(1/x)(5/4)sqrt(39)���i4/sqrt(390))(5/4)sqrt(39)��5/sqrt(10)��(1/2)sqrt(10)
AM��k��6�{�Ȃ̂�
AM��6×(1/2)sqrt(10)���@3sqrt(10)�@//
�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`
X^2�|100X^2�{(55×55×39/64)��0
���@�@�@���@�@�@��
���̕��������߂����ɉ����̂�����ǂ��ł��B
�H�H�B������������Ă�́H
�߂���ꂽ���̂́�����ł��B

���͂���͍��Z���wA�̐}�`��I������Ƌ��ȏ��ɒ藝�̏ؖ����Ƃ��čڂ��Ă��邻���ł��B�����A�ӂ��͐�A�͑I�����Ȃ��炵���A�قƂ�ǂ̎��͖��m�̖��ƂȂ�킯�ł��B���������̎�ʼn����A�Ƃ������ƂȂ̂ł��B
�ؖ��͈ȉ��̂Ƃ���ł��B�������Ă��܂��Ύ��ɊȒP�ł��B
�����A�ؖ���܂�2�i�K�܂Ȃ��Ă͂Ȃ炸�A��1�i�K�ŕ��s���̕⏕���������A��2�i�K�ŎO�p�`�ɊO�ڂ���~�i������⏕���Ƃ����̂��H�j��`���K�v������܂��B
���p����O�ɁA���͋C�Â��̂��H�Ƃ����Ƃ���ł��傤���B

���̎O�p�`����ABC�Ƃ��A��A��2��������BC�̌�_��M�Ƃ��܂��B
�e�ӂ̒������AAB��a�AAC��b�AAM��f�ABM��d�AMC��e�Ƃ��܂��B�ic�͑啶����C�ƕ���킵���̂Ŏg�p���܂���B�j

C��ʂ�MA�ɕ��s�Ȑ��ƁABA��A�̕����ɐL���������Ƃ̌�_��D�Ƃ��܂��B
���s��AM��CD������2����BC�y��BD�ɂ����āAd�Fe��a�Fc�����藧���܂��B
�܂�AM��CD�͕��s�Ȃ̂Ł�BAC����ADC�A���l�Ɂ�MAC��ACD�A
���Ƃ��Ɓ�BAC����MAC�i�p��2�����j�Ȃ̂ŁA��ADC����ACD�A
���������ć�ACD��2���ӎO�p�`�Ȃ̂ŁAc��b�ɂȂ�܂��B
d�Fe��a�Fb
a��12�Ab��10�Ad�{e��11����A
12e��10d�Ae��11�|d��������ƁA
12(11�|d)��10d�A132�|12d��10d�A22d��132�A
����������d��6�Ae��11�|6��5�A�ƂȂ�܂��B

����
��ABC�̊O�ډ~��`���AAM�̉������Ɖ~���Ƃ̌�_��E�Ƃ��܂��B
EM��g�AEB��h�Ƃ��܂��B
��BEA����MCA�i�~���p�j�A��BAE��MAC�i�p��2�����j
���������ć�BEA�䇙AGC�ɂȂ�܂��B
������Aa�F(f�{g)��f�Fb
�܂��A��BME�䇙AMC�Ȃ̂ŁAg�Fe��d�Ff
���������āAf^2�{fg��ab��12×10��120
�܂��Afg��de��6×5��30
�����f^2�{30��120�Af^2��90�Af��3sqrt(10)��0�A
AM�̒������@3sqrt(10)�@�ł��B
�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`
���āA�߂���ꂽ�̂́A�����̕����ł͂Ȃ��āA
�u���Ⴀ�A���̒藝�ɋC�Â��Ȃ�������A���ɂǂ�ȕ��@�ʼn����̂��낤���H�v�Ƃ����^��������Ă��܂������Ƃł��B
��������I��肻�����Ȃ��v�Z���n�܂���������킯�Ȃ̂ł��B
�Ȃ�Ă��������I�I
�⏕����2�{�����܂����B

��ABC�ɂ����āA�_C�����A�̓����ɐ��������낵��_��P�Ƃ���B
���̐���������ɐL����AB�Ƃ̌�_��D�Ƃ���B
D����AM�ƕ��s�Ȑ�������BC�Ƃ̌�_��E�Ƃ���B
��ABM�䇙DBM�i��BAM����BDE�A��AMB��DEB�A��B�͋��ʁj
���������āA
12�F2��(BE�{EM)�FBE
�܂��A
EM��MC�A
BE�{EM�{MC��BE�{2EM��11
(BE�{EM)��6BE
EM��5BE
BE�{2×5BE��11BE��11
�䂦��BE��1�ABM��6�AMC��5
DE�FAM��2�F12��1�F6�Ȃ̂�
DE��������A�����6�{����悢�B
��ABC�̖ʐς�S�Ƃ���B
t���i10�{11�{12�j/2��33/2�Ƃ����Ƃ�
S��sqrt(t(t�|10)(t�|11)(t�|12))
�@��sqrt(33/2)(13/2)(11/2)(9/2))
�@���i1/4�jsqrt(3×11×13×11×3×3)
�@��(33/4)sqrt(39)
��ADC�̖ʐς�S1�Ƃ����
S1��S×(5/6)��(5/6)(33/4)sqrt(39)
�@�@��(55/8)sqrt(39)
�O�����̒藝����
x^2�{h^2��100
�܂�
xh��S1��(55/8)sqrt(39)
����������
x^2�{(1/x^2)(55×55×39/64)��100
x��0�Ȃ̂�
x^4�|100x^2�{(55×55×39/64)��0
x^2��X�Ƃ����ƁA
X^2�|100X^2�{(55×55×39/64)��0
���̂Ƃ�
X=195/8�A�@X=605/8
����������
x��(11/4)sqrt(10)��8.69����A�@x��(1/4)sqrt(390)��4.93���
5.5��x��0�Ȃ̂�
x��(1/4)sqrt(390)
��DBC�̖ʐ�S2��
S2��(1/6)S��(1/6)(33/4)sqrt(39)��(11/8)sqrt(39)
�����
��DEC�̖ʐ�S3��
S3��(10/11)(11/8)sqrt(39)��(5/4)sqrt(39)
����������
2xk(1/2)��xk��(5/4)sqrt(39)
k��(1/x)(5/4)sqrt(39)���i4/sqrt(390))(5/4)sqrt(39)��5/sqrt(10)��(1/2)sqrt(10)
AM��k��6�{�Ȃ̂�
AM��6×(1/2)sqrt(10)���@3sqrt(10)�@//
�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`
X^2�|100X^2�{(55×55×39/64)��0
���@�@�@���@�@�@��
���̕��������߂����ɉ����̂�����ǂ��ł��B
posted by �p�v���J2020 at 03:00| �i�J�e�S���Ȃ��j
2020�N11��23��
�d�Ԃɂ�
���������l�߂�������ЂƂ�����̂ɁA�Ǝv���Ă��N���l�߂܂���B�����J���Ă��ė₽����C�����ꍞ��Ŋ����̂ɒN������߂܂���B����ł��ĒN������������܂���B�V�^�R���i�E�C���X�̊����g��h�~�̂��߂ɂЂƂ̈ӎ����ς���Ă��܂��B
�u�R���i�Ȃ�Ă����̕��ׁv�ƌ����Ă����ЂƂ����܂����A�E�B���X���Ȃ߂Ă��܂��B�Ȋw���w�����B���Ă������������m�����f����̂͌l�l�ł��B�ƂȂ�ƁA�����ȉ��A����ς⋰�|�������Łu�R���i�Ȃ�Ă����̕��ׁv�Ƃ������t�����܂�āA������������d�lj����Ȃ��Ă��ނЂƂ���ĂɊׂ�A���ȂȂ��Ă������ЂƂ����Ɏ����Ă��܂���������܂���B
�d�Ԃ̒��Ń}�X�N�����Ă��Ȃ��ЂƂ͂ЂƂ�����܂���B���H������l�̂Ȃ��ɂ̓}�X�N�Ȃ��̐l���݂����邱�Ƃ�����܂����A�d�Ԃ̂Ȃ��ł͂ق�100���̃}�X�N���p���ł��B�ʋΎ��ԑтł�����A���̂悤�Ȉӎ��̍����l����荇�킹�Ă���̂�������܂���B�O���������Ƃ����L����t���Ă���̂�������܂���B
�}�X�N�̌��ʂƂ����͎̂v�����ȏ�ɑ傫���Ɗ����Ă��܂��B���N�ꂵ�߂�Ă����ԕ��ǂ̏Ǐ��N�͔��Ɍy���ς݂܂����B�܂��A���N���ׂ��Ђ���������������ɊP���Ƃ܂�Ȃ��Ȃ�ЂƂ��E��ɂ���̂ł����A���N�͂��̏Ǐ���Ă��܂���B
�}�X�N�̌��ʂ͕���܂���B

�u�R���i�Ȃ�Ă����̕��ׁv�ƌ����Ă����ЂƂ����܂����A�E�B���X���Ȃ߂Ă��܂��B�Ȋw���w�����B���Ă������������m�����f����̂͌l�l�ł��B�ƂȂ�ƁA�����ȉ��A����ς⋰�|�������Łu�R���i�Ȃ�Ă����̕��ׁv�Ƃ������t�����܂�āA������������d�lj����Ȃ��Ă��ނЂƂ���ĂɊׂ�A���ȂȂ��Ă������ЂƂ����Ɏ����Ă��܂���������܂���B
�d�Ԃ̒��Ń}�X�N�����Ă��Ȃ��ЂƂ͂ЂƂ�����܂���B���H������l�̂Ȃ��ɂ̓}�X�N�Ȃ��̐l���݂����邱�Ƃ�����܂����A�d�Ԃ̂Ȃ��ł͂ق�100���̃}�X�N���p���ł��B�ʋΎ��ԑтł�����A���̂悤�Ȉӎ��̍����l����荇�킹�Ă���̂�������܂���B�O���������Ƃ����L����t���Ă���̂�������܂���B
�}�X�N�̌��ʂƂ����͎̂v�����ȏ�ɑ傫���Ɗ����Ă��܂��B���N�ꂵ�߂�Ă����ԕ��ǂ̏Ǐ��N�͔��Ɍy���ς݂܂����B�܂��A���N���ׂ��Ђ���������������ɊP���Ƃ܂�Ȃ��Ȃ�ЂƂ��E��ɂ���̂ł����A���N�͂��̏Ǐ���Ă��܂���B
�}�X�N�̌��ʂ͕���܂���B

posted by �p�v���J2020 at 00:00| �i�J�e�S���Ȃ��j
2020�N11��22��
���r�m���̐��`�㐔
���r�m���Ő��`�㐔�����Ă܂��B
�s��ƍs���B������������n�b�L���������������̂ł��B�n�b�L��������ǂ�ȗ��v������̂������ꂻ���ł����A�����X�b�L�������������ł��B
�X�b�L��������A���Ƃ͖Y�ꂿ����č\��Ȃ��̂ł��B�X�b�L�����邱�Ƃ��厖�Ȃ̂ł��B�����������Ƃ�����A�Ƃ����̂��厖�ł��B
������Ȃ��܂܃����������Ă���̂ƁA�Y�ꂿ��������Lj�x�͗������ăX�b�L�������o��������̂Ƃ͉_�D�̍��ł��B
���̂��������������Ă邱�Ƃ������Y�ꂿ�Ⴄ��������܂��B
���̊p�ɂ��č��͂ǂ��������̂��������ł��܂��A���܂ł̐l���̒��Łu���������v�Ǝv�����u�Ԃ��������̂ł��B�D�ɗ������̂ł��B���̃X�b�L�������C�������A�����ȏ�ʂł܂����킢�����̂ł��B
�����������łȂ�����A�ۂ�|�c���ƌ��Ă��܂��B
https://youtu.be/svm8hlhF8PA

�s��ƍs���B������������n�b�L���������������̂ł��B�n�b�L��������ǂ�ȗ��v������̂������ꂻ���ł����A�����X�b�L�������������ł��B
�X�b�L��������A���Ƃ͖Y�ꂿ����č\��Ȃ��̂ł��B�X�b�L�����邱�Ƃ��厖�Ȃ̂ł��B�����������Ƃ�����A�Ƃ����̂��厖�ł��B
������Ȃ��܂܃����������Ă���̂ƁA�Y�ꂿ��������Lj�x�͗������ăX�b�L�������o��������̂Ƃ͉_�D�̍��ł��B
���̂��������������Ă邱�Ƃ������Y�ꂿ�Ⴄ��������܂��B
���̊p�ɂ��č��͂ǂ��������̂��������ł��܂��A���܂ł̐l���̒��Łu���������v�Ǝv�����u�Ԃ��������̂ł��B�D�ɗ������̂ł��B���̃X�b�L�������C�������A�����ȏ�ʂł܂����킢�����̂ł��B
�����������łȂ�����A�ۂ�|�c���ƌ��Ă��܂��B
https://youtu.be/svm8hlhF8PA

posted by �p�v���J2020 at 03:00| �i�J�e�S���Ȃ��j
2020�N11��21��
0���ɒ���
0���ƌ������R���킵�����Ȃ��Ă��܂��܂����B
�}�̂悤�Ɋe�_��A�AB�AC�AD�AP�Ƃ��܂��B
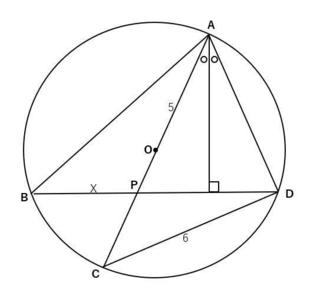
AOC�͒��a�Ȃ̂�
AC��5×2��10
��ADC�͒��aAOC�̉~���p�Ȃ̂Œ��p�ł��B
���p��ACD��2�ӂ̒�����������̂ŁA�O�����̒藝���g����
AD��sqrt(10^2�|6^2)��8
��APD��2���ӎO�p�`�Ȃ̂�
AP��8
�䂦��PC��2
�����Ň�ACD�̖ʐ�S��
S��6×8÷2��24
��DAC�ɂ�����D���璼�aAC�ɐ��������낵��_��T�Ƃ��܂��B
���̐���DT�̒���L�́A
S��24��10×L÷2
�䂦��L��4.8
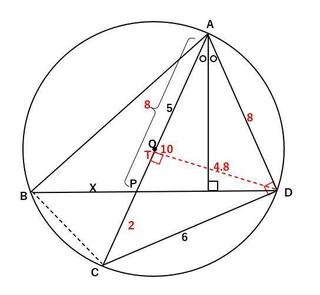
���p��CDT�ɂ����ĕ�CT�̒����́A�O�����̒藝���g����
CT��sqrt(6^2�|(4.8)^2)��(1/10)sqrt(60^2�|48^2)
�@�@��(1/10)sqrt(3600�|2304)
�@�@��(1/10)sqrt(1296)
�@�@��(1/10)sqrt(4^2×9^2)
�@�@��(1/10)×36
�@�@��3.6
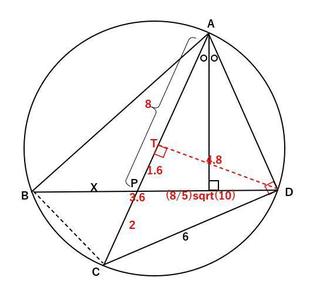
����������TP�̒�����
TP��3.6�|2��1.6
��DPT�ɂ����āAPD�̒����͎O�����̒藝���g����
PD��sqrt(1.6^2�{4.8^2)
�@�@��(1/10)sqrt(16^2�{48^2�j
�@�@��(16/10)sqrt(1�{3^2�j
�@�@��(8/5)sqrt(10)
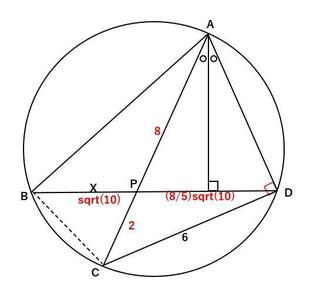
��PBA����PCD(��AD�̉~���p)
��PAB����PDC(��BC�̉~���p)
��BPA����CPD(���p)
���������ć�APB�䇙DPC
�䂦�Ɉȉ��̊W�����藧��
X�FPC��PA�FPD
X��PC×PA/PD
����ɐ��l���������
X��2×8/((8/5)sqrt(10))
�@�@��10/sqrt(10)
�@�@��10sqrt(10)/10
�@�@��sqrt(10)
�䂦��
�@X��sqrt(10)
�ł��B

�}�̂悤�Ɋe�_��A�AB�AC�AD�AP�Ƃ��܂��B

AOC�͒��a�Ȃ̂�
AC��5×2��10

��ADC�͒��aAOC�̉~���p�Ȃ̂Œ��p�ł��B
���p��ACD��2�ӂ̒�����������̂ŁA�O�����̒藝���g����
AD��sqrt(10^2�|6^2)��8
��APD��2���ӎO�p�`�Ȃ̂�
AP��8
�䂦��PC��2
�����Ň�ACD�̖ʐ�S��
S��6×8÷2��24
��DAC�ɂ�����D���璼�aAC�ɐ��������낵��_��T�Ƃ��܂��B
���̐���DT�̒���L�́A
S��24��10×L÷2
�䂦��L��4.8
���p��CDT�ɂ����ĕ�CT�̒����́A�O�����̒藝���g����
CT��sqrt(6^2�|(4.8)^2)��(1/10)sqrt(60^2�|48^2)
�@�@��(1/10)sqrt(3600�|2304)
�@�@��(1/10)sqrt(1296)
�@�@��(1/10)sqrt(4^2×9^2)
�@�@��(1/10)×36
�@�@��3.6

����������TP�̒�����
TP��3.6�|2��1.6
��DPT�ɂ����āAPD�̒����͎O�����̒藝���g����
PD��sqrt(1.6^2�{4.8^2)
�@�@��(1/10)sqrt(16^2�{48^2�j
�@�@��(16/10)sqrt(1�{3^2�j
�@�@��(8/5)sqrt(10)

��PBA����PCD(��AD�̉~���p)
��PAB����PDC(��BC�̉~���p)
��BPA����CPD(���p)
���������ć�APB�䇙DPC
�䂦�Ɉȉ��̊W�����藧��
X�FPC��PA�FPD
X��PC×PA/PD
����ɐ��l���������
X��2×8/((8/5)sqrt(10))
�@�@��10/sqrt(10)
�@�@��10sqrt(10)/10
�@�@��sqrt(10)
�䂦��
�@X��sqrt(10)
�ł��B
posted by �p�v���J2020 at 03:00| �i�J�e�S���Ȃ��j
2020�N11��20��
���������Z�������ɒ��킵�܂���
�������̍��Z��������

�ł����B
�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`
2��5�̌��ɏ���Ă�56��24���r���܂��B
���ꂼ���f�����������܂��B
56��7×2^3
24��3×2^3
2^3��8�Ƃ������������ʂɎ����Ă���̂��C�ɂȂ�܂��B
2^7��128
5^3��125
����Ȃ�@128��2^7�@���@5^3��125
���̑召�W�����������܂܂��ꂼ��𗼕ӂɂ����Ă����Ă��s�����̌����͕ς��Ȃ��̂�
2^7×2^7�@���@5^3×5^3�@���@(2^7)^2�@���@(5^3)^2
(2^7)^2×2^7�@���@(5^3)^2×5^3�@���@(2^7)^3�@���@(5^3)^3
(2^7)^3×2^7�@���@(5^3)^3×5^3�@���@(2^7)^4�@���@(5^3)^4
(2^7)^4×2^7�@���@(5^3)^4×5^3�@���@(2^7)^5�@���@(5^3)^5
(2^7)^5×2^7�@���@(5^3)^5×5^3�@���@(2^7)^6�@���@(5^3)^6
(2^7)^6×2^7�@���@(5^3)^6×5^3�@���@(2^7)^7�@���@(5^3)^7
(2^7)^7×2^7�@���@(5^3)^7×5^3�@���@(2^7)^8�@���@(5^3)^8
������
�@(2^7)^8��2^56
�@(5^3)^8��5^24
���������đ�ӂ̑召�W��
�@2^56�@���@5^24
�ł��B
�`�`�`�`�`�`�`�`�`�`�`�`
2^7��128
5^3��125
�Ȃ̂�
2^7��5^3�{3
���ӂ͓������̂ŁA���ꂼ��8�悵�Ă�������
(2^7�j^8��(5^3�{3)^8
(5^3�{3)^8�̒l�́A5^3��8�悵���l�����傫���̂�
(2^7�j^8��(5^3�{3)^8��(5^3)^8
�����
(2^7�j^8�@���@(5^3)^8
����������
�@2^56�@���@5^24
�ł��B//

�ł����B
�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`
2��5�̌��ɏ���Ă�56��24���r���܂��B
���ꂼ���f�����������܂��B
56��7×2^3
24��3×2^3
2^3��8�Ƃ������������ʂɎ����Ă���̂��C�ɂȂ�܂��B
2^7��128
5^3��125
����Ȃ�@128��2^7�@���@5^3��125
���̑召�W�����������܂܂��ꂼ��𗼕ӂɂ����Ă����Ă��s�����̌����͕ς��Ȃ��̂�
2^7×2^7�@���@5^3×5^3�@���@(2^7)^2�@���@(5^3)^2
(2^7)^2×2^7�@���@(5^3)^2×5^3�@���@(2^7)^3�@���@(5^3)^3
(2^7)^3×2^7�@���@(5^3)^3×5^3�@���@(2^7)^4�@���@(5^3)^4
(2^7)^4×2^7�@���@(5^3)^4×5^3�@���@(2^7)^5�@���@(5^3)^5
(2^7)^5×2^7�@���@(5^3)^5×5^3�@���@(2^7)^6�@���@(5^3)^6
(2^7)^6×2^7�@���@(5^3)^6×5^3�@���@(2^7)^7�@���@(5^3)^7
(2^7)^7×2^7�@���@(5^3)^7×5^3�@���@(2^7)^8�@���@(5^3)^8
������
�@(2^7)^8��2^56
�@(5^3)^8��5^24
���������đ�ӂ̑召�W��
�@2^56�@���@5^24
�ł��B
�`�`�`�`�`�`�`�`�`�`�`�`
2^7��128
5^3��125
�Ȃ̂�
2^7��5^3�{3
���ӂ͓������̂ŁA���ꂼ��8�悵�Ă�������
(2^7�j^8��(5^3�{3)^8
(5^3�{3)^8�̒l�́A5^3��8�悵���l�����傫���̂�
(2^7�j^8��(5^3�{3)^8��(5^3)^8
�����
(2^7�j^8�@���@(5^3)^8
����������
�@2^56�@���@5^24
�ł��B//
posted by �p�v���J2020 at 03:00| �i�J�e�S���Ȃ��j