2020年11月24日
憑りつかれる
別に霊に憑かれているわけではなく、角の2等分線に憑かれているのです。
??。何言っちゃってんの?
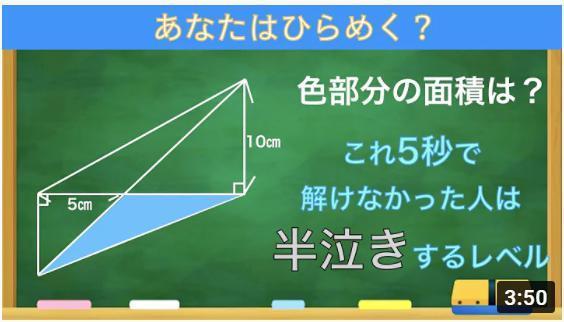
憑りつかれた正体は↓これです。
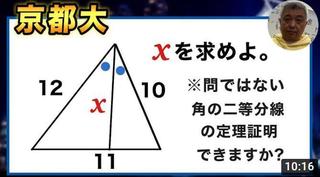
実はこれは高校数学Aの図形を選択すると教科書に定理の証明問題として載っているそうです。ただ、ふつうは数Aは選択しないらしく、ほとんどの受験生は未知の問題となるわけです。これを入試の受験場で解け、ということなのです。
証明は以下のとおりです。分かってしまえば実に簡単です。
ただ、証明を得るまで2段階を踏まなくてはならず、第1段階で平行線の補助線を引く、第2段階で三角形に外接する円(これも補助線というのか?)を描く必要があります。
問題用紙を前に、受験生は気づくのか?というところでしょうか。
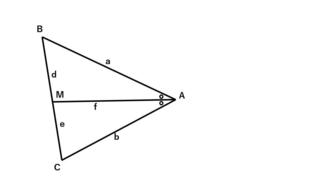
問題の三角形を⊿ABCとし、∠Aの2等分線とBCの交点をMとします。
各辺の長さを、AB=a、AC=b、AM=f、BM=d、MC=eとします。(cは大文字のCと紛らわしいので使用しません。)
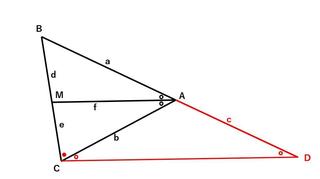
Cを通りMAに平行な線と、BAをAの方向に伸ばした直線との交点をDとします。
平行線AMとCDを横切る2直線BC及びBDにおいて、d:e=a:cが成り立ちます。
またAMとCDは平行なので∠BAC=∠ADC、同様に∠MAC=ACD、
もともと∠BAC=∠MAC(角の2等分)なので、∠ADC=∠ACD、
したがって⊿ACDは2等辺三角形なので、c=bになります。
d:e=a:b
a=12、b=10、d+e=11から、
12e=10d、e=11-dを代入すると、
12(11-d)=10d、132-12d=10d、22d=132、
したがってd=6、e=11-6=5、となります。
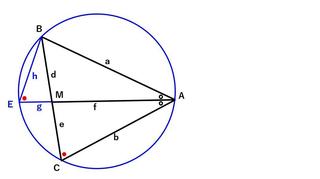
次に
⊿ABCの外接円を描き、AMの延長線と円周との交点をEとします。
EM=g、EB=hとします。
∠BEA=∠MCA(円周角)、∠BAE=MAC(角の2等分)
したがって⊿BEA∽⊿AGCになります。
これより、a:(f+g)=f:b
また、⊿BME∽⊿AMCなので、g:e=d:f
したがって、f^2+fg=ab=12×10=120
また、fg=de=6×5=30
よってf^2+30=120、f^2=90、f=3sqrt(10)>0、
AMの長さは 3sqrt(10) です。
~~~~~~~~~~~~~~~~~~~~~~~
さて、憑りつかれたのは、ここの部分ではなくて、
「じゃあ、この定理に気づかなかったら、他にどんな方法で解くのだろうか?」という疑問をもってしまったことです。
ここから終わりそうもない計算が始まっちゃったわけなのです。
なんてこったい!!
補助線を2本引きました。
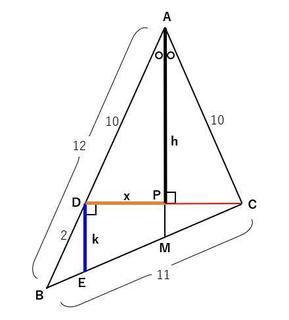
⊿ABCにおいて、点Cから∠Aの二等分線に垂線を下ろし交点をPとする。
この垂線をさらに伸ばしてABとの交点をDとする。
DからAMと平行な線を引きBCとの交点をEとする。
⊿ABM∽⊿DBM(∠BAM=∠BDE、∠AMB=DEB、∠Bは共通)
したがって、
12:2=(BE+EM):BE
また、
EM=MC、
BE+EM+MC=BE+2EM=11
(BE+EM)=6BE
EM=5BE
BE+2×5BE=11BE=11
ゆえにBE=1、BM=6、MC=5
DE:AM=2:12=1:6なので
DEが分かれば、それを6倍すればよい。
⊿ABCの面積をSとする。
t=(10+11+12)/2=33/2としたとき
S=sqrt(t(t-10)(t-11)(t-12))
=sqrt(33/2)(13/2)(11/2)(9/2))
=(1/4)sqrt(3×11×13×11×3×3)
=(33/4)sqrt(39)
⊿ADCの面積をS1とすると
S1=S×(5/6)=(5/6)(33/4)sqrt(39)
=(55/8)sqrt(39)
三平方の定理から
x^2+h^2=100
また
xh=S1=(55/8)sqrt(39)
したがって
x^2+(1/x^2)(55×55×39/64)=100
x>0なので
x^4-100x^2+(55×55×39/64)=0
x^2=Xとおくと、
X^2-100X^2+(55×55×39/64)=0
このとき
X=195/8、 X=605/8
したがって
x=(11/4)sqrt(10)=8.69・・・、 x=(1/4)sqrt(390)=4.93・・・
5.5>x>0なので
x=(1/4)sqrt(390)
⊿DBCの面積S2は
S2=(1/6)S=(1/6)(33/4)sqrt(39)=(11/8)sqrt(39)
よって
⊿DECの面積S3は
S3=(10/11)(11/8)sqrt(39)=(5/4)sqrt(39)
したがって
2xk(1/2)=xk=(5/4)sqrt(39)
k=(1/x)(5/4)sqrt(39)=(4/sqrt(390))(5/4)sqrt(39)=5/sqrt(10)=(1/2)sqrt(10)
AMはkの6倍なので
AM=6×(1/2)sqrt(10)= 3sqrt(10) //
~~~~~~~~~~~~~~~~
X^2-100X^2+(55×55×39/64)=0
↑ ↑ ↑
この方程式をめげずに解くのがしんどいです。
??。何言っちゃってんの?
憑りつかれた正体は↓これです。

実はこれは高校数学Aの図形を選択すると教科書に定理の証明問題として載っているそうです。ただ、ふつうは数Aは選択しないらしく、ほとんどの受験生は未知の問題となるわけです。これを入試の受験場で解け、ということなのです。
証明は以下のとおりです。分かってしまえば実に簡単です。
ただ、証明を得るまで2段階を踏まなくてはならず、第1段階で平行線の補助線を引く、第2段階で三角形に外接する円(これも補助線というのか?)を描く必要があります。
問題用紙を前に、受験生は気づくのか?というところでしょうか。

問題の三角形を⊿ABCとし、∠Aの2等分線とBCの交点をMとします。
各辺の長さを、AB=a、AC=b、AM=f、BM=d、MC=eとします。(cは大文字のCと紛らわしいので使用しません。)

Cを通りMAに平行な線と、BAをAの方向に伸ばした直線との交点をDとします。
平行線AMとCDを横切る2直線BC及びBDにおいて、d:e=a:cが成り立ちます。
またAMとCDは平行なので∠BAC=∠ADC、同様に∠MAC=ACD、
もともと∠BAC=∠MAC(角の2等分)なので、∠ADC=∠ACD、
したがって⊿ACDは2等辺三角形なので、c=bになります。
d:e=a:b
a=12、b=10、d+e=11から、
12e=10d、e=11-dを代入すると、
12(11-d)=10d、132-12d=10d、22d=132、
したがってd=6、e=11-6=5、となります。

次に
⊿ABCの外接円を描き、AMの延長線と円周との交点をEとします。
EM=g、EB=hとします。
∠BEA=∠MCA(円周角)、∠BAE=MAC(角の2等分)
したがって⊿BEA∽⊿AGCになります。
これより、a:(f+g)=f:b
また、⊿BME∽⊿AMCなので、g:e=d:f
したがって、f^2+fg=ab=12×10=120
また、fg=de=6×5=30
よってf^2+30=120、f^2=90、f=3sqrt(10)>0、
AMの長さは 3sqrt(10) です。
~~~~~~~~~~~~~~~~~~~~~~~
さて、憑りつかれたのは、ここの部分ではなくて、
「じゃあ、この定理に気づかなかったら、他にどんな方法で解くのだろうか?」という疑問をもってしまったことです。
ここから終わりそうもない計算が始まっちゃったわけなのです。
なんてこったい!!
補助線を2本引きました。

⊿ABCにおいて、点Cから∠Aの二等分線に垂線を下ろし交点をPとする。
この垂線をさらに伸ばしてABとの交点をDとする。
DからAMと平行な線を引きBCとの交点をEとする。
⊿ABM∽⊿DBM(∠BAM=∠BDE、∠AMB=DEB、∠Bは共通)
したがって、
12:2=(BE+EM):BE
また、
EM=MC、
BE+EM+MC=BE+2EM=11
(BE+EM)=6BE
EM=5BE
BE+2×5BE=11BE=11
ゆえにBE=1、BM=6、MC=5
DE:AM=2:12=1:6なので
DEが分かれば、それを6倍すればよい。
⊿ABCの面積をSとする。
t=(10+11+12)/2=33/2としたとき
S=sqrt(t(t-10)(t-11)(t-12))
=sqrt(33/2)(13/2)(11/2)(9/2))
=(1/4)sqrt(3×11×13×11×3×3)
=(33/4)sqrt(39)
⊿ADCの面積をS1とすると
S1=S×(5/6)=(5/6)(33/4)sqrt(39)
=(55/8)sqrt(39)
三平方の定理から
x^2+h^2=100
また
xh=S1=(55/8)sqrt(39)
したがって
x^2+(1/x^2)(55×55×39/64)=100
x>0なので
x^4-100x^2+(55×55×39/64)=0
x^2=Xとおくと、
X^2-100X^2+(55×55×39/64)=0
このとき
X=195/8、 X=605/8
したがって
x=(11/4)sqrt(10)=8.69・・・、 x=(1/4)sqrt(390)=4.93・・・
5.5>x>0なので
x=(1/4)sqrt(390)
⊿DBCの面積S2は
S2=(1/6)S=(1/6)(33/4)sqrt(39)=(11/8)sqrt(39)
よって
⊿DECの面積S3は
S3=(10/11)(11/8)sqrt(39)=(5/4)sqrt(39)
したがって
2xk(1/2)=xk=(5/4)sqrt(39)
k=(1/x)(5/4)sqrt(39)=(4/sqrt(390))(5/4)sqrt(39)=5/sqrt(10)=(1/2)sqrt(10)
AMはkの6倍なので
AM=6×(1/2)sqrt(10)= 3sqrt(10) //
~~~~~~~~~~~~~~~~
X^2-100X^2+(55×55×39/64)=0
↑ ↑ ↑
この方程式をめげずに解くのがしんどいです。
【このカテゴリーの最新記事】
-
no image