2020擭11寧21擔
0亾偵挧愴
0亾偲尒偨傜夆慠挧愴偟偨偔側偭偰偟傑偄傑偟偨丅
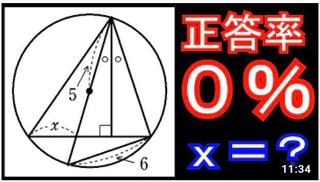
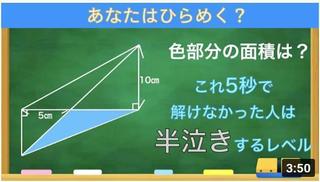
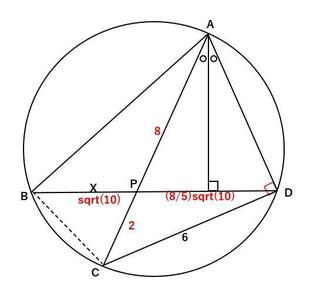
恾偺傛偆偵奺揰傪A丄B丄C丄D丄P偲偟傑偡丅
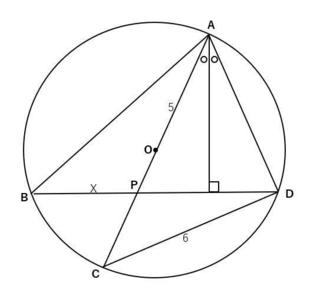
AOC偼捈宎側偺偱
AC亖5×2亖10
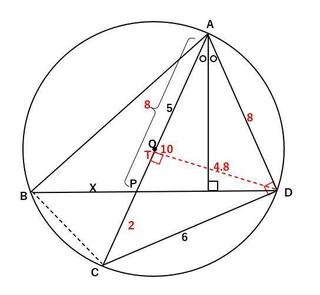
佢ADC偼捈宎AOC偺墌廃妏側偺偱捈妏偱偡丅
捈妏嚈ACD偺2曈偺挿偝偑暘偐傞偺偱丄嶰暯曽偺掕棟傪巊偭偰
AD亖sqrt(10^2亅6^2)亖8
嚈APD偼2摍曈嶰妏宍側偺偱
AP亖8
備偊偵PC亖2
偙偙偱嚈ACD偺柺愊S偼
S亖6×8÷2亖24
嚈DAC偵偍偄偰D偐傜捈宎AC偵悅慄傪壓傠偟岎揰傪T偲偟傑偡丅
偙偺悅慄DT偺挿偝L偼丄
S亖24亖10×L÷2
備偊偵L亖4.8
捈妏嚈CDT偵偍偄偰曈CT偺挿偝偼丄嶰暯曽偺掕棟傪巊偭偰
CT亖sqrt(6^2亅(4.8)^2)亖(1/10)sqrt(60^2亅48^2)
丂丂亖(1/10)sqrt(3600亅2304)
丂丂亖(1/10)sqrt(1296)
丂丂亖(1/10)sqrt(4^2×9^2)
丂丂亖(1/10)×36
丂丂亖3.6
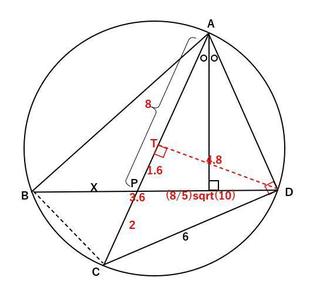
偟偨偑偭偰TP偺挿偝偼
TP亖3.6亅2亖1.6
嚈DPT偵偍偄偰丄PD偺挿偝偼嶰暯曽偺掕棟傪巊偭偰
PD亖sqrt(1.6^2亄4.8^2)
丂丂亖(1/10)sqrt(16^2亄48^2乯
丂丂亖(16/10)sqrt(1亄3^2乯
丂丂亖(8/5)sqrt(10)
佢PBA亖佢PCD(屖AD偺墌廃妏)
佢PAB亖佢PDC(屖BC偺墌廃妏)
佢BPA亖佢CPD(懳捀妏)
偟偨偑偭偰嚈APB佷嚈DPC
備偊偵埲壓偺娭學偑惉傝棫偮
X丗PC亖PA丗PD
X亖PC×PA/PD
偙傟偵悢抣傪戙擖偡傞偲
X亖2×8/((8/5)sqrt(10))
丂丂亖10/sqrt(10)
丂丂亖10sqrt(10)/10
丂丂亖sqrt(10)
備偊偵
丂X亖sqrt(10)
偱偡丅

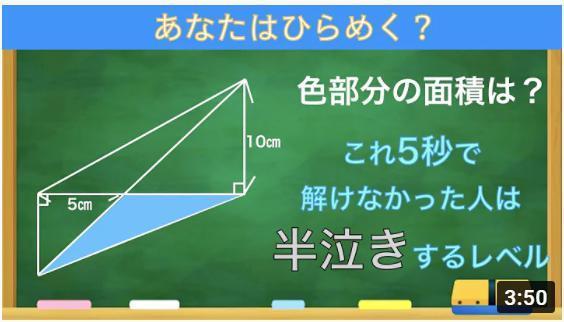
恾偺傛偆偵奺揰傪A丄B丄C丄D丄P偲偟傑偡丅

AOC偼捈宎側偺偱
AC亖5×2亖10

佢ADC偼捈宎AOC偺墌廃妏側偺偱捈妏偱偡丅
捈妏嚈ACD偺2曈偺挿偝偑暘偐傞偺偱丄嶰暯曽偺掕棟傪巊偭偰
AD亖sqrt(10^2亅6^2)亖8
嚈APD偼2摍曈嶰妏宍側偺偱
AP亖8
備偊偵PC亖2
偙偙偱嚈ACD偺柺愊S偼
S亖6×8÷2亖24
嚈DAC偵偍偄偰D偐傜捈宎AC偵悅慄傪壓傠偟岎揰傪T偲偟傑偡丅
偙偺悅慄DT偺挿偝L偼丄
S亖24亖10×L÷2
備偊偵L亖4.8
捈妏嚈CDT偵偍偄偰曈CT偺挿偝偼丄嶰暯曽偺掕棟傪巊偭偰
CT亖sqrt(6^2亅(4.8)^2)亖(1/10)sqrt(60^2亅48^2)
丂丂亖(1/10)sqrt(3600亅2304)
丂丂亖(1/10)sqrt(1296)
丂丂亖(1/10)sqrt(4^2×9^2)
丂丂亖(1/10)×36
丂丂亖3.6

偟偨偑偭偰TP偺挿偝偼
TP亖3.6亅2亖1.6
嚈DPT偵偍偄偰丄PD偺挿偝偼嶰暯曽偺掕棟傪巊偭偰
PD亖sqrt(1.6^2亄4.8^2)
丂丂亖(1/10)sqrt(16^2亄48^2乯
丂丂亖(16/10)sqrt(1亄3^2乯
丂丂亖(8/5)sqrt(10)

佢PBA亖佢PCD(屖AD偺墌廃妏)
佢PAB亖佢PDC(屖BC偺墌廃妏)
佢BPA亖佢CPD(懳捀妏)
偟偨偑偭偰嚈APB佷嚈DPC
備偊偵埲壓偺娭學偑惉傝棫偮
X丗PC亖PA丗PD
X亖PC×PA/PD
偙傟偵悢抣傪戙擖偡傞偲
X亖2×8/((8/5)sqrt(10))
丂丂亖10/sqrt(10)
丂丂亖10sqrt(10)/10
丂丂亖sqrt(10)
備偊偵
丂X亖sqrt(10)
偱偡丅
亂偙偺僇僥僑儕乕偺嵟怴婰帠亃
-
no image