パプリカ2020の部屋

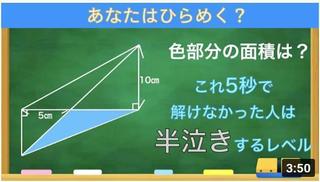
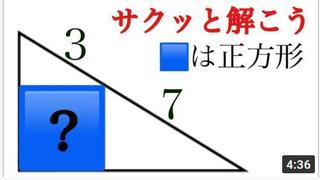
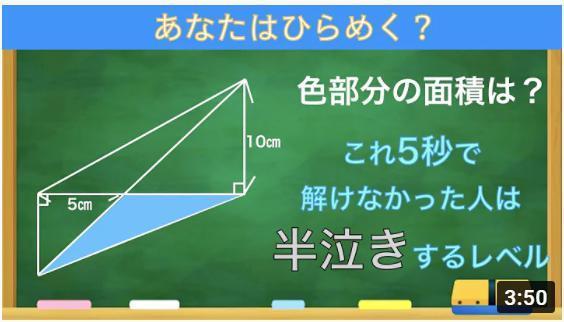
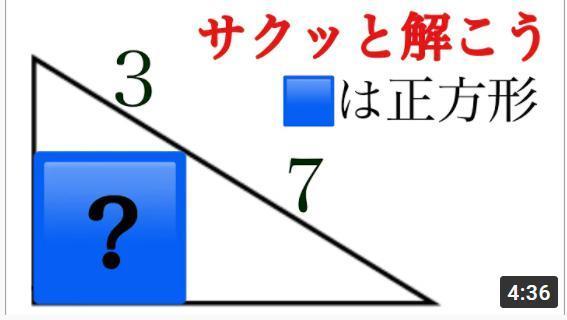
奮闘中の高校入試問題は



でした。

〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜〜

2と5の肩に乗ってる56と24を比較します。

それぞれを素因数分解します。
56＝7×2^3
24＝3×2^3

2^3＝8という数字を共通に持っているのが気になります。

2^7＝128
5^3＝125

これなら　128＝2^7　＞　5^3＝125

この大小関係をたもったままそれぞれを両辺にかけていっても不等号の向きは変わらないので

2^7×2^7　＞　5^3×5^3　→　(2^7)^2　＞　(5^3)^2
(2^7)^2×2^7　＞　(5^3)^2×5^3　→　(2^7)^3　＞　(5^3)^3
(2^7)^3×2^7　＞　(5^3)^3×5^3　→　(2^7)^4　＞　(5^3)^4
(2^7)^4×2^7　＞　(5^3)^4×5^3　→　(2^7)^5　＞　(5^3)^5
(2^7)^5×2^7　＞　(5^3)^5×5^3　→　(2^7)^6　＞　(5^3)^6
(2^7)^6×2^7　＞　(5^3)^6×5^3　→　(2^7)^7　＞　(5^3)^7
(2^7)^7×2^7　＞　(5^3)^7×5^3　→　(2^7)^8　＞　(5^3)^8

ここで
　(2^7)^8＝2^56
　(5^3)^8＝5^24

したがって題意の大小関係は
　2^56　＞　5^24

です。

〜〜〜〜〜〜〜〜〜〜〜〜

2^7＝128
5^3＝125
なので
2^7＝5^3＋3

両辺は等しいので、それぞれ8乗しても等しい
(2^7）^8＝(5^3＋3)^8

(5^3＋3)^8の値は、5^3を8乗した値よりも大きいので
(2^7）^8＝(5^3＋3)^8＞(5^3)^8

よって
(2^7）^8　＞　(5^3)^8

したがって
　2^56　＞　5^24

です。//