パプリカ2020の部屋

YOUTUBEを見ていたら面白い問題を見つけました。
某有名企業の入社試験問題だそうです。
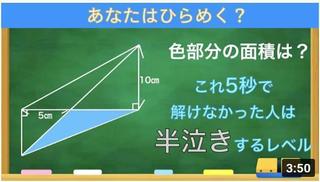
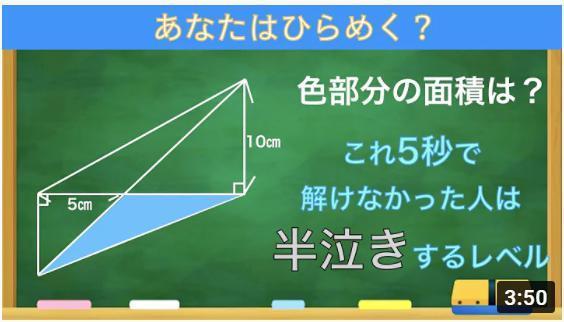
「Ｑ．次の図形の面積を求めよ」


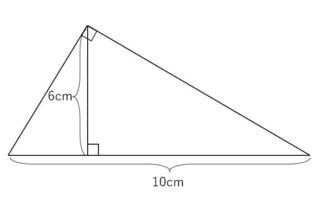
見た瞬間「底辺×高さ÷2」で完璧。30平方ｾﾝﾁﾒｰﾄﾙ。
この答えは間違いだそうです。・・・え？計算は合ってるじゃあないですか（怒！

正解は「このような三角形は存在しない」だそうです。
ん？？？
10cmの底辺を直径として、三角形が直角を持つ頂点をとおる円を描きます。


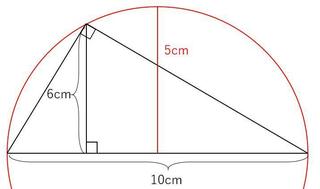
この三角形の高さにあたる部分は、どうがんばってもこの円の半径より小さくなります。この円の半径は直径÷2で、10cm÷2＝5cmですから、高さが6cmの三角形にはなりえないのです。


YOUTUBEでは別の方法で説明していました。

要は、入社試験に小学生でも解ける問題を出すことから疑え、問題という前提を疑え、というものでした。

ひとを騙す時はこのようなありもしない前提をさもあるように始めるのがコツかもしれません。前提から始まるわけですからそれ以降の筋道は整然とするはずです。
オレオレ詐欺も「電話をしてきたのは息子だ」という前提を作り出すために、事前に小芝居を打つのです。