ていへんかけるたかさわるに

HP-42S の複素数の機能を, 平面上のベクトルに関する問題に応用する例題の続き.
最初の例は内積だったが, 今度は外積を使用する.

例: 複素数の外積
マニュアルでは, この例題の単位としてポンドとインチが用いられている. さしあたりそれに従って説明する.

図のような, 長さと角度が $r = 5 \,\mathrm{in} \,\angle 50^{\circ}$ のレバーを考える. このレバーの取っ手部分に $F = 300 \,\mathrm{lb} \cdot \mathrm{in}/\mathrm{s}^2 \,\angle 205^{\circ}$ の力を加えたときのモーメント $M$ を求める.



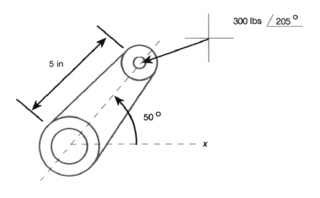
モーメント $M$ は動径ベクトル $r$ と力 $F$ の外積として
\begin{equation*}
\newcommand{\Ar}[1]{\mathrm{Ar}(#1)}
\newcommand{\ar}{\mathrm{ar}}
\newcommand{\arop}{\Opp{\mathrm{ar}}}
\newcommand{\Func}[2]{\mathrm{Func}(#1,#2)}
\newcommand{\Hom}{\mathrm{Hom}}
\newcommand{\Id}[1]{\mathrm{id}_{#1}}
\newcommand{\Mb}[1]{\mathbf{#1}}
\newcommand{\Mr}[1]{\mathrm{#1}}
\newcommand{\Ms}[1]{\mathscr{#1}}
\newcommand{\Ob}[1]{\mathrm{Ob}(#1)}
\newcommand{\Opp}[1]{{#1}^{\mathrm{op}}}
\newcommand{\Pos}{\mathbf{Pos}}
\newcommand{\q}{\hspace{1em}}
\newcommand{\qq}{\hspace{0.5em}}
\newcommand{Rest}[2]{{#1}|{#2}}
\newcommand{\Src}{d^{0,\mathrm{op}}}
\newcommand{\Tgt}{d^{1,\mathrm{op}}}
M = r \times F
\end{equation*} によって求まる. 外積では交換法則は成立しないのでこの順序で計算を行う必要がある.

  MODES  DEG  MODES  POLAR      ; 度・極座標モードの指定.
  5  ENTER  50  COMPLEX         ; 動径ベクトル r を複素数として入力.
  300  ENTER  205  COMPLEX      ; 力ベクトル F を複素数として入力.
  MATRIX  CROSS                 ; 外積 r × F を計算.

$\quad \Rightarrow 633.9274 \,[\Mr{lb} \cdot \Mr{in} \cdot \Mr{s}^{-2} \cdot \Mr{in}]$

結果が正の実数なので, モーメントは大きさが約 634 で, 方向が図の面に垂直に上を向いていることになる.

この結果を MKS 単位系に変換すると,
\begin{align*}
633.9274 \,[\Mr{lb} \cdot \Mr{in} \cdot \Mr{s}^{-2} \cdot \Mr{in}]
&= 633.9274 \,[\Mr{lb} \cdot 1/12 \,\Mr{ft} \cdot \Mr{s}^{-2} \cdot 1/12 \,\Mr{ft}] \\
&= 633.9274 \,[0.3732 \,\Mr{kg} \cdot (1/12) \cdot 0.3048 \,\Mr{m} \cdot \Mr{s}^{-2} \cdot (1/12) \cdot 0.3048 \,\Mr{m}] \\
&= 633.9274 \,[2.4077 \cdot 10^{-4} \,\Mr{kg} \cdot \Mr{m} \cdot \Mr{s}^{-2} \cdot \Mr{m}] \\
&= 0.1526 \,[\Mr{N} \cdot \Mr{m}]
\end{align*} となる.