こばとの数学基礎講座02 素数と合成数
KOBATO です! いよいよ夏休みですね!皆さん、今年の夏はどう過ごされますか?
こばとは8月に小春ちゃん、沙希ちゃんたちと海に行く予定です。今からちょー楽しみです!
それでは本日の講義を始めます。
今回は自然数の中でも特別な数である「素数」を扱います。「素数ぐらい知ってるよ。学校で習ったよ」という人も、ぜひ読んでみてください。たくさんの数学者が熱い眼差しを注ぐ素数には多くの謎が秘められていて、学校の教科書にはのっていないことがまだまだいっぱいあるのです。今回の講座ではそのあたりのことを少しだけ、そしてなるべく易しく解説してみますね。
素数の解説に入る前に、ちょっとだけ「九九」のおさらいをしてみましょう。「ばかにしないで!」と怒らないでくださいね。説明をわかりやすくするためなので少しご辛抱ください。では 14 という数を掛け算の形に直してみてください。小学校3年生の子でも「簡単だよ!」てことで、
14 = 7 × 2
となりますね。でも、もう1つ別の形もありますよね?
14 = 14 × 1
です。「なーんだ、くだらない」と思うかもしれませんが、実はここに重要な意味が潜んでいるのです。では練習のためにもう1問。25 を掛け算の形に直してみてください。
25 = 5 × 5
25 = 25 × 1
ですね。ちょー簡単です。では次は 7 という数を二通りに分解してください。え? できない? そうですね。
7 = 7 × 1
とするのが、7 を掛け算で表す唯一の方法です。他にも 2 や 3, 或いは 5 などはどうですか? 同じですね。どれも
2 = 2 × 1
3 = 3 × 1
5 = 5 × 1
一通りの方法でしか掛け算にできません。こういう数のことを「素数」といいます。それ以外の数は「合成数」と呼ぶことにします。
「じゃあ、1 も 1 = 1 × 1 だから素数だね!」ということにしたいところですが、残念ながら 1 だけは素数の仲間には入れないことにします。特別な数として取り分けておくことにします。そうすることでとても便利になるからです。先ほどの問題を「14 を素数の掛け算で表しなさい」と少し手直ししてみると、1 は素数としないに決めたのですから、
14 = 7 × 2
と一通りに書くことしかできませんね。25 は
25 = 5 × 5
となります。練習のために 36 もやってみましょう。
36 = 6 × 6 = 3 × 2 × 3 × 2
と4つの素数に分解できました。 3×3 のように同じ数を掛けることをを 3 2 のように表すことにすれば、もう少しすっきりして、
36 = 3 2 × 2 2
となります。こういう分け方を「素因数分解」といいます。それでは「 7 を素数の積に直しなさい」という問題はどうですか? 7 × 1 の形はもう禁止ですから、「できません」と答えるしかありませんね。だから、1 を素数でないことにすれば、
素数:掛け算の形に表せない数
合成数:掛け算の形に表せる数
というように決まりが簡単になります。
前回は数学に出てくる色々な数を分類しましたね。今回は自然数をさらに細かく、
1, 素数, 合成数
というふうに三種類に分けることができました。もうこれ以上細かく分けることはできません。
さて、1 は素数ではない特別な数ですが、2 は素数の中の特別な素数です。それは 2 だけが素数の中でただ一つの偶数であるということです。このことを「 2 は偶素数である」といいます。他の偶数は必ず 2 で割り切れてしまいますから、絶対に素数ではありえませんね。2 以外の素数は必ず奇数です。
ある数を見て、それが素数であるのか、そうでないのかは、小さい数の場合は意外と直感でわかったりします。上でも言ったように 2 以外の偶数なら合成数です。「九九」に登場する数であれば、それも合成数ですね。それではいくつか練習してみましょう。
11 は素数ですか? 合成数ですか?
もちろん素数ですね。どんなに頑張っても 11 を他の数の掛け算で表すことなんてできません。次の問題です。
26 は素数ですか? 合成数ですか?
偶数なので簡単に「合成数だよ」と答えられます。26 = 2 × 13 です。13 は直感で素数と判断できます。
63 は素数ですか? 合成数ですか?
ちょっと素数っぽい気がしますけど罠ですよ。これは九九に出てくる数です。7 × 9 = 63 なので素数ではありません。合成数です。
それにしても、これを一つ一つ確認していくのは大変ですね。そこで「エラトステネスのふるい」という方法を使って 2 から 100 までの数の中にある素数を見つけ出してみます。エラトステネスさんは大昔の偉い数学の先生です。
と、その前に。もしかすると若い人は「ふるい」を知らないかもしれないので説明しておきますね。「ふるい」というのは、枠に細かい網を張って(テニスのラケットのようなものを想像してください)、そこに大きさの様々な粉粒どさっとを入れて、大きい物と小さい物を選り分けるという昔の道具です。この言葉を知らないと、「素数をふるい分ける」ということをイメージできません。こばとはもう千年も生きているので、「ふるい」は身近にありましたよ。
それでは「エラトステネスのふるい」を使って素数を見つけましょう! まず 2 以外の偶数には用がないので、さっさと消えてもらって、奇数だけを並べます。
02 03 05 07 09 11 13 15 17 19
21 23 25 27 29 31 33 35 37 39
41 43 45 47 49 51 53 55 57 59
61 63 65 67 69 71 73 75 77 79
81 83 85 87 89 91 93 95 97 99
3 は素数ですが、3の倍数は合成数です。なのでこれを全部消します。
02 03 05 07
41 43
61
素数の 5 を残し、5の倍数を消します。
02 03 05 07
41 43
61
素数の 7 を残し、7の倍数を消します。
02 03 05 07
41 43
61
はい、出来上がり! 上に残っている数が素数です。
全部で 25 個ありますね。改めて並べておきましょう。
02, 03, 05, 07, 11, 13, 17, 19, 23, 29,
31, 37, 41, 43, 47, 53, 59, 61, 67, 71,
73, 79, 83, 89, 97
実は素数は無限に存在することが証明されています(記事の最後に証明をのせておきます)。無限にあるので、百億年かかっても全ての素数を見つけることはできません。
素数に限らず、偶数だって無限に存在します。n を自然数とすれば、偶数は 2n という式で表せます。奇数なら 2n + 1 です。ところが、素数を表す式は見つかっていません。大昔から、ものすごく頭のいい数学者たちが必死になって見つけようとしてきたのですが、その夢は現代でも叶えられていません。式で表せないので、次にどこに素数が出て来るのか予測が難しいのです。「素数はだいたいこれぐらいの密度で分布しているよ」という分布関数などが考えられたりもしましたが、あくまで近似的なもので、完全ではありませんし、密度がわかったところで位置が予測できるわけでもありません。
とはいえ、現代ではコンピューターの力を借りることができるので、とんでもない桁数の素数が見つかっています。現在判明している最大の素数は米セントラルミズーリ大の数学者グループが発見した1742万5170桁の数です。ひゃあ! もうどんな数なのか想像することもできませんね!
最後に「数学が得意だよ!」という人のための少しだけ難しいお話を付け加えておきます。
「素数は無限に存在するよ!」ということの証明
数学が得意な高校生(あるいは中学生でも)にとってはこの証明はびっくりするぐらい簡単です。素数の数が有限であると仮定しますね。その素数を並べて、
p 1, p 2, ・・・・・・ p n
としておきます。上の素数を使って、
N = p 1 p 2・・・・・・ p n + 1
という数を作ります。これはどの p n とも異なる数ですから合成数のはずです。だからこの数を割り切る素数が p 1, p 2 , ・・・・・・ p n の中に必ず存在するはずです。
いえ、しかし、どう考えても、どの素数で割っても必ず 1 が余ってしまいますよ。割り切れません。矛盾していますね。なので上の仮定が間違っていたということで、素数はやっぱり無限に存在するのです(証明終わり)。
素数の分布
先ほどお話した分布関数の具体的な形です。p(x) ≒ x / logx
と、式の形自体は簡単です。p(x) は x 以下の数の中に含まれる素数の数を表しています。素数なので 2≦x となり、分母が 0 になることはありません。数が増えていくと少しずつ疎らになっていくことがわかります。エクセルでグラフを描くとこんなふうになります。
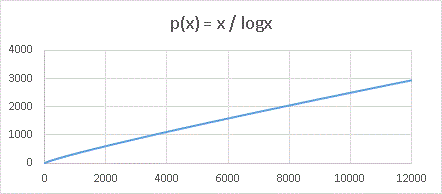
グラフから目分量で読み取ると、4000 以下の数に含まれる素数の数は 1100 個ぐらい、12000 以下だと 3000 個ぐらいですから、密度はそれぞれ約 28%, 25% というぐあいに微妙に小さくなっていることがわかります。log x がとても緩やかな関数なので、密度の減り方はとってもゆっくりです。
これで今日の講義はおしまいです!
次回の『こばとの数学基礎講座3 指数計算』でお会いしましょう!
(次回はけっこう簡単な内容だよ)