こばとの数学基礎講座06 指数関数のグラフと極限
ひゃあ! 猛暑ですね! 外を飛んでいるだけで暑さのあまり墜落してしまいそうです。皆さんも体調には十分気をつけてくださいね。こばとは念願の小さな簪(かんざし)を手に入れました。小春ちゃんと小夜子さんにも見せてあげました! 浴衣と簪で花火大会に行ってきましたよ! ちょー楽しかったです!それでは夏の暑さに負けずに数学しましょう!
まずは前回のおさらいです。指数法則は
a > 0, a 0 = 1
a x + y = a x a y
( a x) y = a xy
( a b ) x = a x b x
のように定義されていましたね。今回は
y = a x
という関数を考えるのですが、その際にもう1つだけ a ≠ 1 という条件を加えておくことにします。普通に計算するなかでは a = 1 でも 1 x = 1 となるだけで何の支障もないのですが、関数の場合は y = 1 という直線になってしまい、これではとても指数関数とは呼べません。煩わしいので a = 1 は外しておくことにします。
それでは、さっそくエクセルで y = 2 x のグラフを描いてみましょう。エクセルで指数を出力させるには、"= 2^□" (□は数値あるいは指定されたセル番号)と入力します。
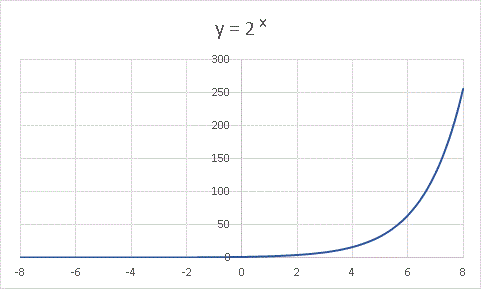
−8 ≦ x ≦ 8 の範囲で描いています。0 < x では右肩上がりの関数です。x に対する y の増加率はとても大きく、x = 4 で y = 2 4 = 16, x = 8 では y = 2 8= 256 となります! x が 1000 とか 10000 などの値をとれば、y は途方もなく大きな値をとることになります。では x を無限大(∞)にすれば y はどうなりますか? そうです。y も無限大になりますね。これを lim(リミット)という記号を使って、
と書きます。また、このような状態のことを「 x → ∞ のとき、y は極限値をもたずに発散する」と表現します。
x < 0 ではほとんど 0 に見えますね。このままでは見えにくいので、範囲を絞ってグラフを拡大してみます。
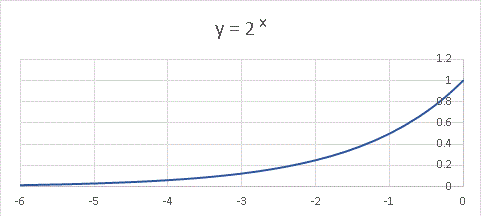
エクセルではこういうことも簡単にできちゃいます。 y = 2 0 = 1 から少しずつ減って(格好良い言葉では逓減すると言います!)、0 に近づいていっていますね。 x を負の無限大(−∞)にすると、y は 0 になるということです。これを先ほどの記号を使って、
と表します。この状態を「 x → −∞ のとき、y は極限値 0 をとる」と表現します。
次は a = 1 / 2 の場合を考えてみます。
y = ( 1 / 2 ) x
ちょっと書き直してみましょう。これまで指数計算で学んできたように、1 / 2 = 2 −1 ですから、( a x) y = a x y の公式を使って、上の関数は
y = ( 2 −1 ) x = 2 −x
と表せます。y = 2 x の x の部分が −x になっていますね。y = 2 −x に 1, 2, 3, ・・・・・・ と正の値を入れれば、それは y = 2 x に −1, −2, −3, ・・・・・・ の値を入れたことと同じです。y = 2 −x に負の値を入れれば、 y = 2 x に正の値を入れたことと同じになります。つまり、y = 2 x とy = 2 −x は、y 軸に対して対称な関数であるはずです。では実際にエクセルのグラフで確かめてみましょう。
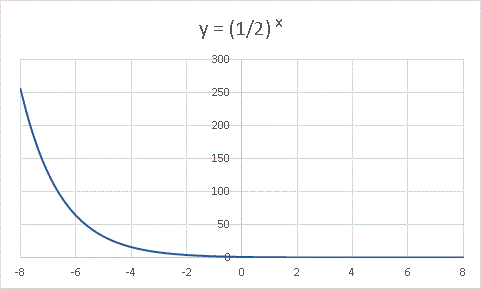
確かに対称なグラフになっていますね。さて、ここでグラフをじっと見つめながらちょっと勘をはたらかせてみてください。y = 2 x と y = 2 −x を足し加えるとどうなりますか? 左右対称のお椀のようなグラフがイメージできると思います。確かめてみましょう。
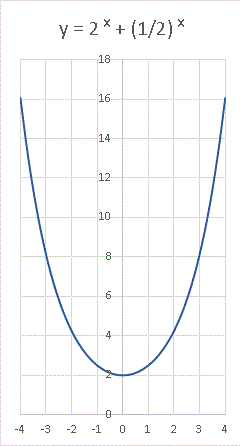
縦軸のスケールを変えた( x と y の目盛の大きさを同じにしています)ので少し印象が変わるかもしれませんが、確かに左右対称のグラフが現れました。 a = 2 の代わりに、ネーピアの数と呼ばれる e = 2.71828 ・・・・・・ という無理数で y = e x を定義し、y = e −x を加えて 2 で割った関数を coshx という記号で定義します。coshx はハイパボリック・コサイン(hypabolic cosine)の略です:
coshx = [ e x + e −x ] / 2
また、両関数を引いて 2 で割った関数を sinhx(hypabolic sine)で定義します:
sinhx = [ e x - e −x ] / 2
coshx や sinhx のような関数を双曲線関数と呼びます。双曲線関数はエクセルの中に用意されています。"= cosh()", "= sinh()" のように入力し、()の中に数値か指定されたセル番号を入れます。グラフを見てみましょう。
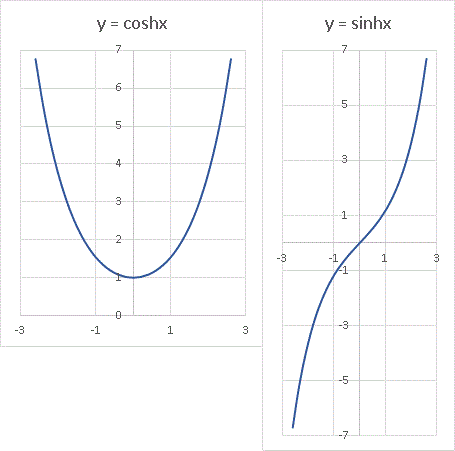
二次関数に形が似ていますけど、全くの別物なので注意してください。sinhx は正負ともに極限を持たない(∞、−∞ に発散する)グラフです。なぜこうなるのでしょうか? もう一度 sinhx の定義式を見てみます。
coshx = [ e x + e −x ] / 2
ここで x → ∞ とすると、 e −x は 0 になり、第1項のみが残ります。つまり x が大きいところではあたかも e x / 2 のように振る舞うということです。これは普通の指数関数ですね。 x → −∞ とすると、逆に2つ目の項だけが残り、 − e −x / 2 となります。これは e x / 2 を y 軸対称に折り返し、(負号によって)上下を逆さまにした形ですね。だから全体として上のグラフのような形になるわけです。
来週あたりには暑さも和らぐといいですね。次回は指数関数を用いて等比数列を講義する予定です。それではまたお会いしましょう!
こばとの数学基礎講座07 指数関数の底と極限の関係
かき氷を食べすぎてお腹を壊しました・・・・・・。皆さんも冷たい物の取り過ぎには十分注意してくださいね。今回はちょっと予定を変更して指数関数の極限について講義します。前回は y = 2 x について極限を調べましたね。今回は一般的な y = a x について、a をパラメーターとしてグラフを変化させてその形と極限がどのように移り変わっていくかを見ていきます。今回は計算が一切なく、グラフを眺めているだけで終わりますので、気楽にのんびりと数学を楽しんでください。ではまず、 y = 1.1 x という関数のグラフを描いてみましょう。
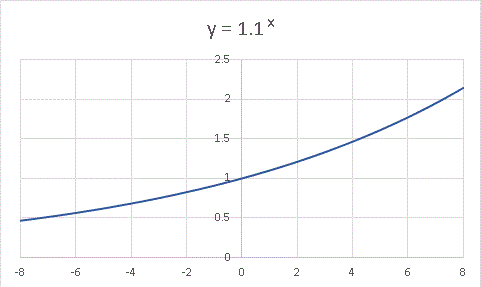
底 a は 1 よりほんの少し大きく、 y = 2 x に比べると値の変化は緩やかではありますけど、やはり x → +∞ で発散し、 x → -∞ で 0 に収束することに変わりはありません。もう少し a を小さくして 1 に近づけてみましょう。 y = 1.01 x のグラフです:
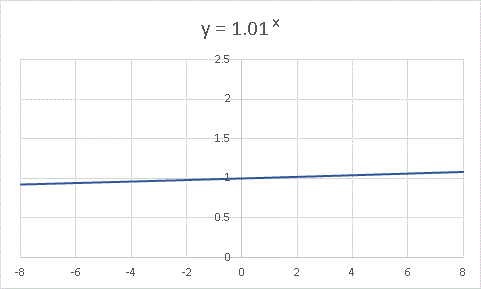
「ちょーのんびりした」関数ではありますけど、それでもやっぱり勾配があるので、 x を正の無限大までもっていけば y は無限大になりますし、x を負の無限大まで引っ張って行けば y も 0 になるだろうな、ということがわかります。前回の講義で「 a = 1 は指数関数の定義から外しますよ」といいましたが、変遷の途中としてあえて y = 1 x = 1 のグラフを描いてみます。
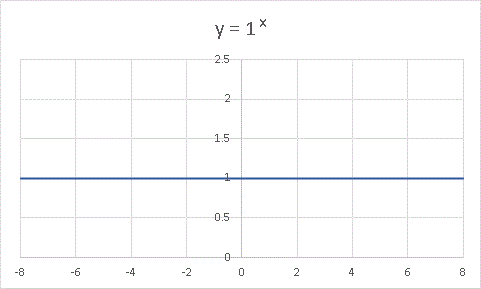
当たり前といえば当たり前ですが、この関数は発散しません。 0 にも収束しません。 x → ±∞ で 1 に収束します。 y の値はどこでも 1 なのですから、「 1 に収束する」というのも何だかおかしな言い方なのですが、数学用語を用いればそういう表現になるのです。お次は 1 より少し小さな値を底とする y = 0.99 x です。
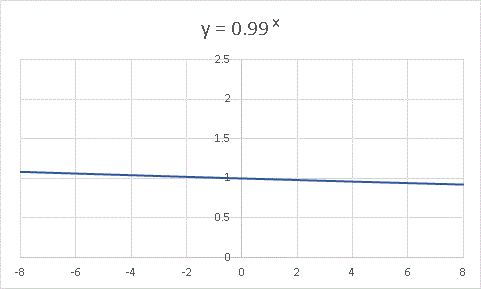
傾きが逆転しました。したがって、今度は x → -∞ で発散し、 x → +∞ で 0 に収束します。最後に y = 0.9 x です。
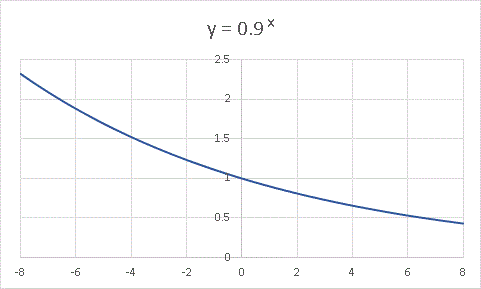
特に説明の必要もないですね。
上の変遷を見てわかるように、 y = a x のグラフは a が 1 よりほんの僅かでも大きければ x → +∞ で発散し、 x → -∞ で 0 に収束します。逆に a が 1 より小さければ x → -∞ で発散し、 x → +∞ で 0 に収束するということになります。
下にまとめておきますね。
a > 1 のとき
a < 1 のとき
これは次回の無限等比数列でも使いますので、ちょっとだけ頭の隅に残しておいてくださいね。それではまたお会いしましょう!