こばとの数学基礎講座08 無限等比数列(1) [公比 r > 0]
今年はとんでもない猛暑でしたが、8月後半は急に気温が下がってすでに秋の気配さえ漂わせています。そうなると何だか急に寂しい気分になりますね。でも学生の皆さんはこれから新学期です。「学校、めんどいなー」なんて思わずに気持ちを入れ替えて勉強してくださいね。受験生の皆さんはそろそろ「ひゃー、どうしよう!?」という感じになってきますかねー。もともとこの基礎講座は「高校生向けに夏休みの間だけだよ」という趣旨で始めたものですが、もう少しだけ延長しますので空いた時間にスマホや PC でのぞいてみてくださいね。指数関数のおさらいです。 y = 2 x のグラフをもう一度載せておきます。
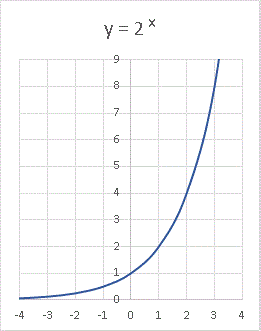
今回扱うのは等比数列です。上のグラフは連続ですが、x = ・・・・・・ -3, -2, -1, 0, 1, 2, 3, ・・・・・・ というように x が整数数部分のところだけ取り出してプロットすると、次のようなグラフが描けます。
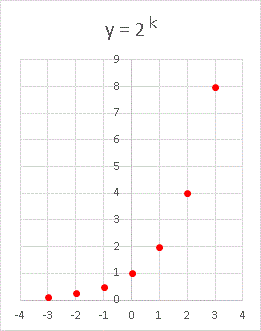
x = k とおいて改めて関数を書き表すと、
f (k) = 2 k
です。 具体的な値を書き出してみると、
・・・・・・
f (-3) = 1 / 8
f (-2) = 1 / 4
f (-1) = 1 / 2
f (0) = 1
f (1) = 2
f (2) = 4
f (3) = 8
f (4) = 16
・・・・・・
f (k) = 2 k
・・・・・・
f (-3) = 1 / 8
f (-2) = 1 / 4
f (-1) = 1 / 2
f (0) = 1
f (1) = 2
f (2) = 4
f (3) = 8
f (4) = 16
・・・・・・
f (k) = 2 k
・・・・・・
のようになり、正負に無限に続く数が並びます。次に上の数の並びから、k = 1 以降を抜き出します:
2, 4, 8, 16 ・・・・・・
そして改めて自然数 n で番号を振ります:
a 1 = 2
a 2 = 4
a 3 = 8
a 4 = 16
・・・・・・
a n = 2 n
a 2 = 4
a 3 = 8
a 4 = 16
・・・・・・
a n = 2 n
最初の数 2 を初項、 2 n を一般項といいます。また指数関数において底であった 2 は数列では公比と呼びます。今は初項として f(1) = 1 を選びましたが、実のところその選び方は任意です。たとえば、初項を f(0) = 1 を選択すると、
1, 2, 4, 8, ・・・・・・
という数列が得られますが、そこに振る番号は自然数と決まっているので、n と対応する a1 = 1 は 手前に 1 つずれます:
a 1 = 1
a 2 = 2
a 3 = 4
a 4 = 8
a 5 = 16
・・・・・・
a n = 2 n-1
a 2 = 2
a 3 = 4
a 4 = 8
a 5 = 16
・・・・・・
a n = 2 n-1
初項を k = -3 すなわち f (-3) = 1 / 8 を選んでも一向に構いません。その場合の数列は:
a1 = 1 / 8
a 2 = 1 / 4
a 3 = 1 / 2
a 4 = 1
a 5 = 2
・・・・・・
a n = 2 n-4
a 2 = 1 / 4
a 3 = 1 / 2
a 4 = 1
a 5 = 2
・・・・・・
a n = 2 n-4
となります。振られる番号が大きくずれて一般項 a n の書き方が異なっていますね。このように、元の横軸 x の値と番号 n は基本的にずれていますが、1 対 1 の対応があることには注意してください。
前回、指数関数の極限値に少し触れましたが、x が飛び飛びの値 k をとってもそれは全て指数関数のグラフ上にある点ですから、±∞ の振る舞いは変わるはずもなく、上のグラフで明らかなように n → + ∞ のときは an → ∞、 n → -∞ のときは an → 0 となります。これは数列の抜き出し方(初項の選び方)には関係なく、常に成り立ちます。極限をとる操作に比べれば番号の多少のずれなど何ほどでもないということです。
次はもう少し複雑な関数 y = 3・2 x を見てみます。整数部分をプロットしたグラフを描くと:
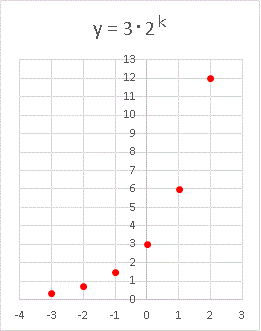
このようになります。k = 0 以降を抜き出して番号を振ると:
a 1 = 3
a 2 = 6
a 3 = 12
a 4 = 48
・・・・・・
an = 3・2 n-1
a 2 = 6
a 3 = 12
a 4 = 48
・・・・・・
an = 3・2 n-1
初項 3 、公比 2 の数列ですね。一般項の指数の肩が n-1 であることに注意してください。初項として f(1) = 6 を選択すると、
a 1 = 6
a 2 = 12
a 3 = 48
a 4 = 146
・・・・・・
an = 3・2 n
a 2 = 12
a 3 = 48
a 4 = 146
・・・・・・
an = 3・2 n
のように 1 つずれます。この選び方だと一般項の指数の肩は n となります。
それでは一般化して関数 y = a・r x を考えます。前回までは指数の底に a を用いていましたが、今は数列に対応させるために a は定数とし、代わりに r を底に用いていることに注意してください。もう1つ、とても大切な点を1つだけ。指数関数では r > 0 が条件でしたね。その理由は y = (-2) x のような関数を定義すると、たとえば x = 1 / 2 のとき、y = √-2 = √2 i のように虚数が現れてしまうからです。しかし数列の場合、指数は自然数ですから、底は負であっても y が虚数になることはありません。したがって r < 0 の場合も扱うことはできるのですが、その数列は正負が交互に入れ替わるために、ちょっとややこしいです。したがって、それは次回で扱うことにして、今回は r > 0 に限定しておきます。
f (0) = a・r 0 = a
f (1) = a・r 1
f (2) = a・r 2
・・・・・・
f (k) = a・r k
・・・・・・
f (1) = a・r 1
f (2) = a・r 2
・・・・・・
f (k) = a・r k
・・・・・・
というように数を抜き取ります。 k = 0 で始まる数の並びに改めて自然数 n を用いて 1 から番号を振ります:
a 1 = a・r 0 = a
a 2 = a・r 1 = a・r
a 3 = a・r 2 = a・r 2
・・・・・・
a n = a・r n-1
・・・・・・
a 2 = a・r 1 = a・r
a 3 = a・r 2 = a・r 2
・・・・・・
a n = a・r n-1
・・・・・・
これが等比数列の一般項の表し方です。指数部分が n から1つずれていることに注意してください。
さて、前回解説したように、 y = r x のグラフは r が 1 より大きければ x → +∞ で発散します。逆に r が 1 より小さければ x → +∞ で 0 に収束します。もちろんそれは数列においても同じように成り立ちます。
a n = r n (今回は r ≧ 0)において、 n → +∞ としたとき、
0 ≦ r < 1 a n → 0
r = 1 a n → 1
1 < r a n → ∞
r = 1 a n → 1
1 < r a n → ∞
上の収束条件は a n = a・r n-1 の形にも適用できます。先にも述べたように、肩の部分の番号のずれは全く気にすることはありません。 r = 1 のときは a に収束し、 0 < r < 1 のときは 0 に収束します。1 < r なら発散です。ただ1つだけ注意しなくてはならないのは、r = 0 の場合で、これはそもそも等比数列とは呼ばれません(等比数列と宣言しなければ、a n = r nという数列自体の定義は可能です)。 a n = a・r n-1 の形にも書けません。番号 n は 1 から順に入れるので、n = 1 のときに 0 0 が生じてしまいますが、これは定義されない数式です。私もたまにこういう間違った数式をエクセルに入力して「エラーですよ!」と返されます。機械にそう言われると何だかむかつきますね。「ちょっと間違えただけじゃん!」と言い返したくなります。まあともかく、 r = 0 の数列は 0 がずっと並ぶだけの数列なので、 a n = 0 と記述されます。もちろん、 n → +∞ としても a n → 0 となるので、収束条件そのものは同じです。
こばとの数学基礎講座09 無限等比数列(2) [公比 r < 0]
今回は無限等比数列の2回目。公比 r < 0 の場合を扱います。まずは r < -1 の例を見ます。初項 1 、公比 -3/2 = -1.5 の数列a n = (-3/2) n-1
を考えてみます。さっそくエクセルでグラフを描いてみましょう。
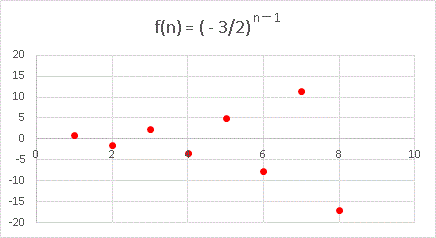
n = 1 から n = 8 までプロットしています。正負に激しく振動する関数ですが、前回説明したように x が飛び飛びの値(自然数)であれば、y の値に虚数が現れることなく、ともかくもこのようにグラフが描けるわけです。グラフを見ると、 n → ∞ のときに ±∞ となることがわかります。「発散かな?」と思えますが、こういう場合は発散ではなく a n の「極限値は存在しない」、或いは「振動」と言います。
今回は、前回とは逆に離散関数 f(n) から対応する連続関数 f(x) を探してみます。
f(n) は n = 1, 3, 5, ・・・・・・のときに指数部分の n-1 は 0, 2, 4, ・・・・・・となり、一般項に現れている負号をキャンセルしています。したがって、n が奇数の場合に対応する連続関数 f(x) は、
f(x) = (2/3) x-1 [1]
となります。肩の部分は x-1 ではなく x と置きなおしても構いませんが、その場合は抜き取る番号もずらす必要があります。今はわかりやすくそのまま x-1 としておきます。
n = 2, 4, 6, ・・・・・・の場合は、
f(n) = (-2/3) n-1 = (-1) n-1 (2/3) n-1
のように変形して、結局は [1] に負号をつけた関数
g(x) = -(2/3) x-1 [2]
を得ることになります。それでは [1] と [2] を x が負の領域まで拡大して描いてみましょう。
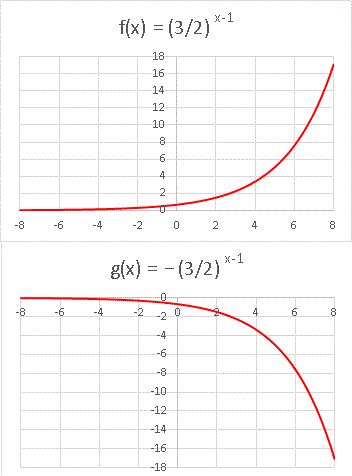
f(n) に対応する2つの連続関数 f(x), g(x) が得られました。f(x) から x = 1, 3, 5, ・・・ 2m-1 ・・・ を抜き取り、g(x) から x = 2, 4, 6, ・・・ 2m ・・・ を抜き取れば数列 f(n) が得られることになります。
次に -1 < r < 0 の例として初項 1 、公比 -1 / 2 = -0.5 の数列
a n = (-1/2) n-1
を考えてみます。
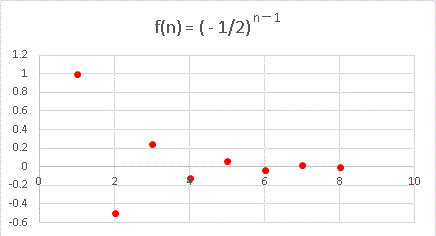
正負に振動しながら 0 に収束する関数です。先程と同じように定義域を拡大した2つの関数を作ってみると、
f(x) = (1/2) x-1 [3]
g(x) = -(1/2) x-1 [4]
g(x) = -(1/2) x-1 [4]
となり、グラフは次のようになります。
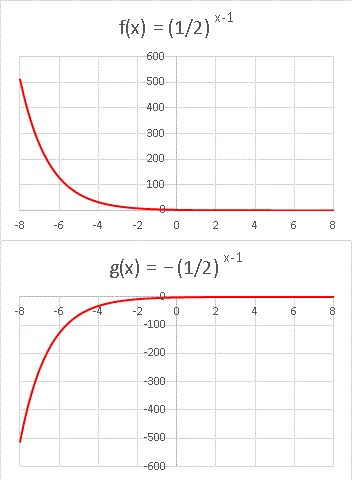
f(x) から奇数番号を、g(x) から偶数番号を抜き取れば数列 a n = (-1/2) n-1 を得ることができます。
最後に収束条件をまとめておきます。 n → ∞ としたときに、 r < -1 なら極限値は存在せず、-1 < r < 0 なら a n → 0 (収束)ですね。さらにこれを前回の r > 0 の場合とまとめると、
n → ∞ のとき:
-1 < r < 1 a n → 0
r = 1 a n → 1
1 < r a n → ∞
r < -1 極限値なし
r = 1 a n → 1
1 < r a n → ∞
r < -1 極限値なし
ちょっとややこしくて覚えにくいかもしれませんが、大切なのは、数列 r n の収束条件は -1 < r ≦ 1 であるということです。これさえ覚えておけば、数学Ⅲにおいて色々な所で応用できます。