[Alt] + [PageDown] 1 画面右にスクロール
[Alt] + [PageUp] 1 画面左にスクロール
ディリクレの積分核(N → ∞ でデルタ関数になります)
下の式で定義される関数を ディリクレの積分核 といいます。
N = 10 でグラフを書いてみるとこうなります。
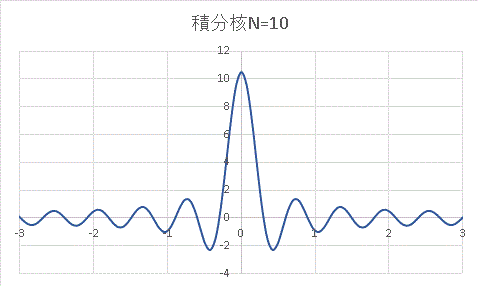
原点で大きなピークを持ち、左右で急速に減衰してゆきます。N → ∞ でよく知られた デルタ関数 になることが知られています。コンピューターでは無限大を扱えないので、ここでは代わりに N = 1000 という大きな値をいれてみましょう。
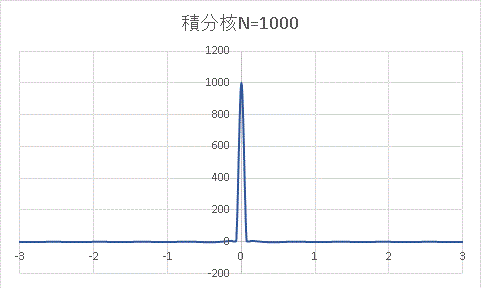
原点で鋭く尖がっていますね。さらに大きな値を N に入れるとほとんど線のようになります。
この関数に sinx を乗じてみます。
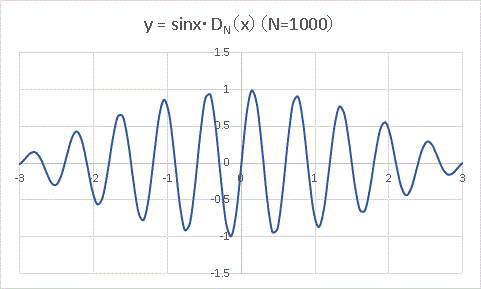
原点を中心とした局所的な波が現れました。積分核には色々な謎が秘められていそうですね。
⇒ なんとなくの数学日記( Blog Cat の専攻は?)