
周期の異なる三角関数を重ね合わせると変なグラフになりますが、それでも 周期関数 であることに変わりはありません。
Excel で概周期関数のグラフを描きます
でも変数に無理数が乗じられていると・・・・・・
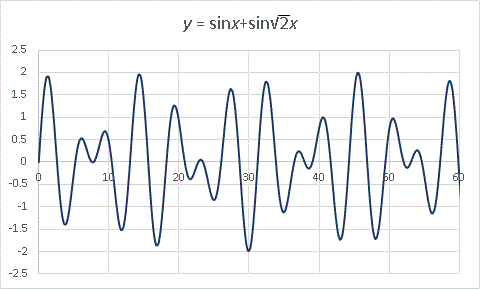
こんなふうになってしまいます。y = sinax + sinbx においてb/aが無理数であるときに、こういうグラフになります。概周期関数 といいます。読んで字のごとく「まあだいたい周期的な関数ですよ」という意味です。「何だそれ?」と思われる読者もおられるかもしれませんが、本当にこう呼ぶのです。でもこれも専門書を探せば載っている関数なので、何か細工しなければブログを終われません。そこで2項目の変数自体を√で抑え込んでみます。
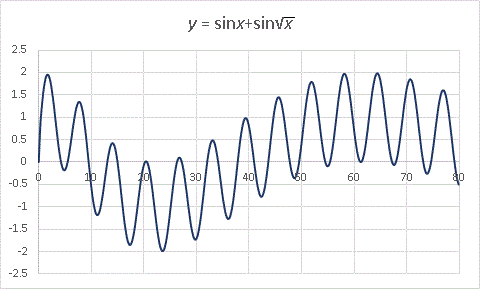
波の山と山、谷と谷を結ぶ線がこれまた波打っています。
思いつきでやってみたのですが、自分でも結構自信作です。
a や b が有理数であれば必ず周期が存在します
y = cos[x + f(x)] の f(x) に sinx を混ぜてみようと思います。まずは y = cos[x + sinx] のグラフです。![cos[x+sinx].gif](/excelmathfunction/file/cos5Bx2Bsinx5D.gif)
山は尖っていて、底は平坦になっていますね。
次は y = cos[x + cosx + sinx] としてみます。
![cos[x+cosx+sinx].gif](/excelmathfunction/file/cos5Bx2Bcosx2Bsinx5D.gif)
少し複雑な波形が現れました。
sin の位相を変えて y = cos[x + cosx + sin(x/3)] とすると ......
![cos[x+cosx+sinxd3].gif](/excelmathfunction/file/cos5Bx2Bcosx2Bsinxd35D.gif)
何だかよくわからない波形になってしまいました。
しかし、x の範囲を拡大してみると ......

ちゃんと周期があることを確認できますね。
cos(ax) と sin(bx) のみで組み合わされた関数は、a や b が有理数である限りは、どれほど複雑に見えても必ず周期が存在しています。しかし、たとえば
y = cos[x + cosx + sin(√2x)]
のような無理数の混じった関数を作ると

このように周期は壊れてしまいます。
無理関数と三角関数の合成
x に対し f を 1 回作用させた F1 グラフは次のようになります。
無理関数 √x に沿って振動する関数ですね。無理関数と三角関数を単純に足し合わせるだけなら、三角関数の周期はそのまま保存されます。この関数を f でもう 1 回変換し、
F2 = f [F1]
をつくると・・・・・・

周期は消えてしまいました。その原因として考えられるのは、
1. 無理関数の中に三角関数を入れたこと
2. 三角関数の中に無理関数を入れたこと
3. 1 と 2 を重ね合わせたこと
この 3 つしかありません。実のところ、わざわざ調べなくても関数に慣れている人は直感的に 1 と 2 は単純な周期関数を描くことがわかります。どうしても気になる人はエクセルで調べてみてください。結論を言うと、原因は 3 にあります。「三角関数の重ね合わせ sinax + cosbx において、 a と b の比が有理数であれば一定周期が保障され、比が無理数であると周期が乱れて概周期関数になる」ということを説明しましたが、今回のように、より複雑な組合せによって周期が崩壊するケースも色々あります。最後に、 f を 3 回作用させた F3 のグラフをおまけとして載せておきます。
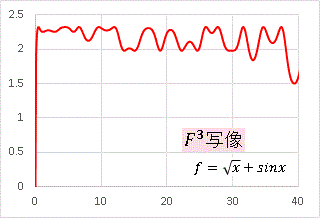
⇒ なんとなくの数学日記(面白いグラフをたくさん載せます)