Excel でノイマン関数(第 2 種円柱関数)のグラフを描きます
ベッセル微分方程式を載せておきます:
この方程式の解の1つがベッセル関数 Jν(x) です。上式は Jν(x) とは独立なもう1つの解が存在します。それはノイマン関数と呼ばれ、次のような式で表されます:
この関数のことをノイマンのベッセル関数、或いは単にベッセル関数と呼ぶこともありますが、紛らわしいので、このブログでは Jν(x) をベッセル関数、 Yν(x) をノイマン関数(第 2 種円柱関数)と呼ぶことに決めておきます。νは全複素数で定義されますが、今の段階ではνが整数の場合のみを扱い、 Y n(x) と記述します。Excel では BESSELY 関数を用いてノイマン関数の値を計算することができます。ではさっそく Y 0(x), Y 1(x), Y 2(x) のグラフを描いてみます。
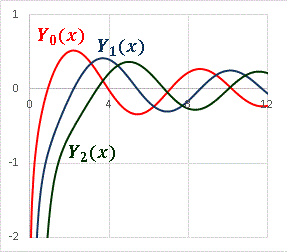
ベッセル関数とよく似ていますが、-∞ から立ち上がってくる特異な形の周期関数です。さて、今回の変形バージョンはノイマン関数 Y 0(x) の変数 x を expx に変換してみます:
![Ynノイマン[expx].gif](/excelmathfunction/file/YnE3838EE382A4E3839EE383B35Bexpx5D.gif)
ノイマン関数よりも早く振幅が減衰する関数です。
x の増加に伴って周期もどんどん短くなっていきます。
ノイマン関数の応用
ノイマン関数 Y0(x) に対数関数を乗じてみましょう: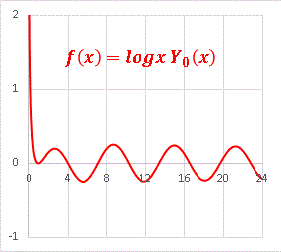
ノイマン関数と logx の負値 が掛け合わされて正値となり、原点近傍で + ∞ から落ちてくる周期関数となります。同じように Y5(x) に対数関数を乗じると・・・・・・
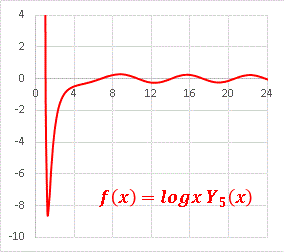
非常に深い谷をもつグラフです。 n が大きくなると、谷はどんどん深くなっていきます。 Excel で描くことも困難なほど、大きな負値をとります。それでも無理に logx Y7(x) 描いてみると・・・・・・
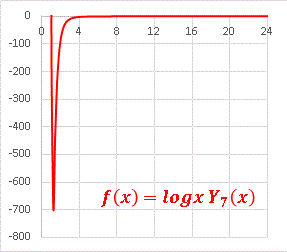
スケールの比較で、他の振動する部分が直線のようになってしまいます。 Y5(x) あたりが限界なのです。
≫ Python ベッセル関数とノイマン関数
⇒ なんとなくの数学日記