合成関数を使って階段グラフを作ります
今回は少し変わった関数の作り方を紹介します。まず最初に、f(x) = x + cosx
という関数をエクセルで描いてみます。
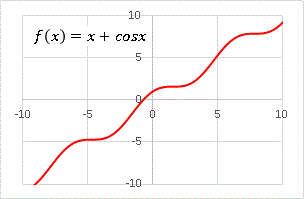
これは予想通りの形ですね。直線 y = x に沿うような周期関数です。それではこの関数をさらに f(x) の中に入れた写像を考えます。つまり、
g(x) = f [f(x)]
= f [x + cosx]
= (x + cosx) + cos(x + cosx)
という入れ子になった関数を考えるわけです。グラフを描くと・・・・・・
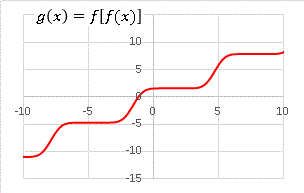
段丘のようなグラフが出現しました。さらに、
h(x) = f[g(x)]
という関数を作ってみましょう:
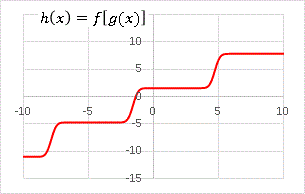
全体的に角ばった形になりましたね。最後にもう1度、
i(x) = f[h(x)]
というように変換すると・・・・・・
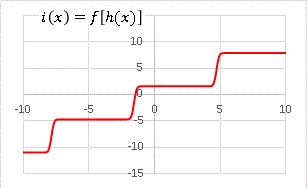
階段の完成です。 i(x) の具体的な表式は相当に複雑になっているはずです。手計算で合成関数を扱うのは至難の業でしょう。しかし Excel を使うと上のような変換は 1 クリックで実行できます。具体的な式の形がわからなくてもグラフを描くことができるのです。元になる関数を変えてみると、色々と面白い関数が出現します。もう少し合成関数で遊んでみましょう。
f(x) = x + cosx + sin2x
という形で変換を定義します。そして x に対し f によって 1 回の変換をほどこした関数を F1 、2 回変換した関数を F2 と書くと約束しておきます:
F 1 = f(x)
F 2 = f [F1]
F 3 = f [F2]
では F3 のグラフをエクセルで描いてみます。
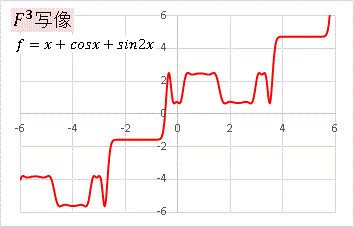
地形のようなグラフが現れましたね。複雑な関数であっても三角関数と1次関数の組合せなので、目を凝らしてみると、きちんと周期があることがわかります。元になる関数を、
g(x) = x + cosx + sin2x + 1
というように少し変えて、g によって 3 回変換した G3 写像のグラフを描いてみると・・・・・・
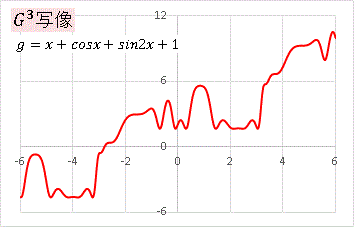
地形の形が変わりましたね。
⇒ なんとなくの数学日記(ナビスコカップ決勝を観ました)