Excel でスターリングの近似式を計算してみます
ともかく、そういう時代には「多少は精度を犠牲にしてもいいから、扱いやすい近似式がほしいよ」ということになります。そこで登場するのが スターリングの近似式 で、次のような形で表されます:この近似式と本物のΓ(x + 1) を同時にグラフで描いてみると・・・・・・

赤で描かれた曲線が正確なΓ(x + 1) , 青がスターリングの近似式です。 x が大きくなるほど精度が良くなっていく(グラフが重なる)ことがわかりますね。スターリングの近似式は漸近展開と呼ばれる手法で導かれた式なのですが、一般に漸近展開はそれほど良い近似を与えません。その中でスターリングの近似式は優等生といっていいぐらいの精度があります。
しかし現代の数値計算では、この見事な近似式も時代の遺物といってもいいかもしれません。極めて正確なガンマ関数がソフトに組み込まれている以上、もはやスターリングの公式を使う理由はないはずです。
実用上はともかくとして、特殊な関数として眺めてみると、かなり面白い式です。 √x x x の部分で急激な x の増加を実現させ、ガンマ関数と比較して行き過ぎた部分を e-x で少し抑えておくという形になっています。変形できそうな部分も色々あり、さらに面白そうな関数を作れる予感があります。あれこれと試行錯誤して色々なグラフを描いてみたのですが、 x と e それぞれの肩に乗っている x を cosx と sinx に置き換えた関数が一番印象に残りました。
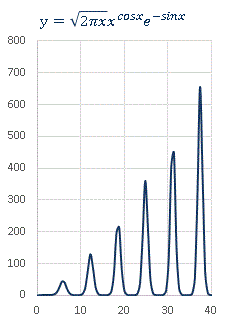
一定周期で鋭いピークが並んでいますね。x の増加と共にピークの値は急速に伸びていきます。しかしどれほど値を伸ばしても、x の肩に乗る三角関数が負の値を取った瞬間、一気に 0 付近まで落ち込むことになります。