[Ctrl] + : 現在の日付を挿入 [Ctrl] + ; 現在の時刻を挿入
螺旋(らせん)行列による座標変換
ベッセル関数を成分とする行列
による変換を線形結合の観点から見直してみます。基底ベクトルは:
となりますが、これは選んだ θ によって角度だけではなく、その大きさも変えてしまいます(記事 52 ベッセル関数を用いた媒介変数表示関数を参照)。 その様子を図示すると次のようになります:
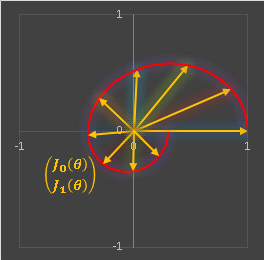
基底ベクトル a は媒介変数で表された関数 (J0(θ), J1(θ)) に沿って螺旋を描きます。 a と b は直交しているので、 b は a に対して + 90°反時計周りに回転させたベクトルとなります。θ = pi / 2 の場合を図示すると:

a と b の張るベクトル空間はやはり直交座標で、θ = π/4 より少し多く元の座標から回転しています。格子の長さは 0.74 倍短くなります。水色の単位ベクトル e を変換すると、赤いベクトル ( -0.095, 1.039) へ移ります。
⇒ なんとなくの数学日記(パーフェクト)