[Ctrl] + ↓ 入力済みセルと空白セルの境界まで移動
[Ctrl] + ↑ 入力済みセルと空白セルの境界まで移動
[Ctrl] + → 入力済みセルと空白セルの境界まで移動
[Ctrl] + ← 入力済みセルと空白セルの境界まで移動
Excel で関数の極大値の移動を調べます
数学Ⅲを習い始めた頃に、
f(x) = x exp(-x), g(x) = x2 exp(-x)
というようなグラフを書く練習をした記憶があると思います。極値が求めやすいですし、形もシンプルで書きやすいですからね。受験を控えた高校 3 年生の人も今の時期(11月)であればもう簡単にグラフを描けると思いますが、一応確認のために微分して極値を求めてみましょう。
f′(x) = (1-x) exp(-x) = 0 ⇒ x = 1
極値は f(1) = 1 / exp(1) = 0.368
f′(0) > 0, f′(∞) < 0 だから上に凸のグラフ
g′(x) = x (x-2) exp(-x) = 0 ⇒ x = 0, 2
極値は g(0) = 0, g(2) = 4 / exp(2) = 0.541
g′(-∞) < 0, g′(0) > 0, g′(∞) < 0 だから
となります。Excel グラフで確認してみましょう。
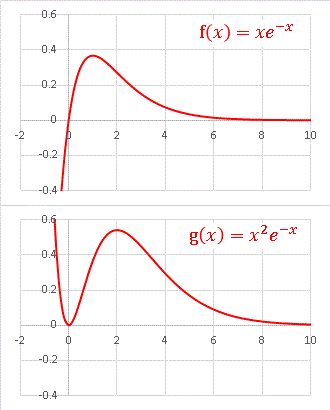
0 < x の範囲で2つのグラフはとてもよく似ていますが、g(x) のほうが極大値は大きく、また極大値をとる x の値も右にずれています。その理由はもちろん exp(-x) という単調減少関数に対して x よりも x2 のほうが値の減少を引き止める力が大きいからです。x の次数をさらに大きくして、
h(x) = x3 exp(-x), i(x) = x5 exp(-x)
を比較してみましょう:
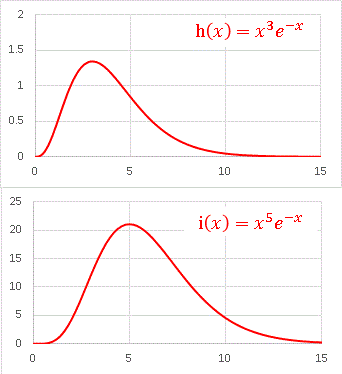
0 < x の範囲で図示してあります。また、上下で縦軸のスケールが変わっていることに注意してください。i(x) の値が大きいので同じスケールで書くと画像が縦長になりすぎてしまいます。やはり極大値は右へ移動していきますね。最後におまけとして
j(x) = x11 exp(-x)
のグラフを描いてみます:

目盛の 6.E+06 という記号は 6.0×106 です。極大値は途轍もなく大きくなっています。しかしそれだけ大きな値をとっているのも関わらず、指数関数 exp(-x) の減少効果はさらに大きく、値を急速に引き下げて行きます( x = 44 で およそ 0.1 )。