波束が移動するグラフ
前回扱った y = xn exp(−x) に sinx を乗じてみます:
f(x) = x sinx exp(−x)
g(x) = x2 sinx exp(−x)
h(x) = x3 sinx exp(−x)
この3つのグラフを軸スケールを統一して並べてみます:
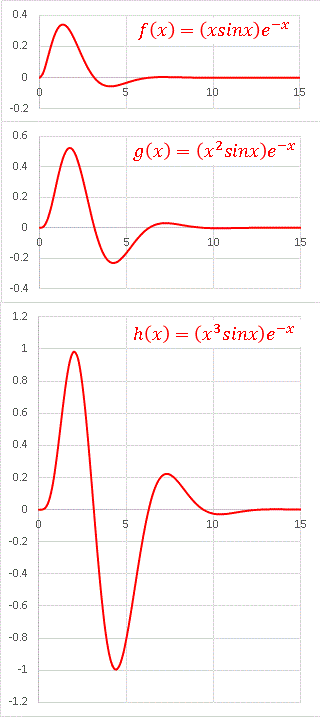
0 < x の範囲を表示しています。最初の山と谷が高く、或いは深くなりつつ右へ移動し、新しい山が立ち上がってくるのがわかります。 x n が sinx と exp(−x) の両方に効いているからです。 n が大きいほど sinx の振幅を増大させ、 exp(−x) の減衰効果を打ち消しています。おまけとして、
i(x) = x11 sinx exp(−x)
j(x) = x20 sinx exp(−x)
のグラフを描いてみます:
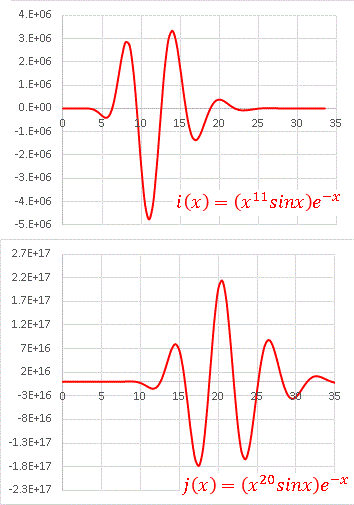
縦軸スケールは変えてあります。振動領域そのものが右に移動していますね。 n によって「波の束」の存在領域が変化してゆくのが、この関数の特徴です。
⇒ なんとなくの数学日記(こばとちゃんは猫が苦手です)