[Shift] + [Space] 行を選択する
[Ctrl] + [Space] 列を選択する
①ルジャンドル多項式 Legendre polynomial
ルジャンドル微分方程式
の解がルジャンドル多項式であり、 [-1, 1] の範囲で
と表されます。ルジャンドル多項式は次の漸化式を満たします:
(2n + 1)xPn(x) = (n + 1)Pn + 1(x) - nPn - 1(x)
具体的には次のような形になります:
P0(x) = 1
P1(x) = x
P2(x) = (3x2 - 1) / 2
P3(x) = (5x3 - 3x) / 2
・・・・・・・・・
②Excel でルジャンドル多項式のグラフを描きます
Excel でグラフを描いてみると・・・・・・
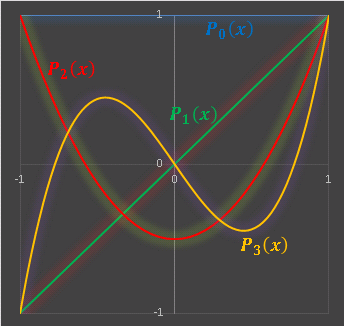
この図からわかるように、一般に
Pn(1) = 1
を満たします。P0(x) において n を大きくしてゆくと、[-1, 1] の区間にたくさんの波が閉じ込められている様子がよくわかります。たとえば P50(x) のグラフを描いてみると・・・・・・
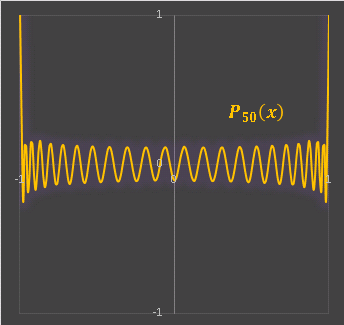
このように区間を限定して 各項の係数をうまく調整すれば、その内部ではあたかも cosx や sinx のように振る舞う疑似的な周期関数を作ることができます。仮にルジャンドル多項式の定義域を拡大したとしても、[-1, 1] を超えた場所に波は存在しないので、単調増加あるいは単調減少となり、そのような関数はほとんど用途がありません。任意の関数を展開するためにも波形の存在する区間に限っておく必要があります。別記事にある正規化されたエルミート多項式 u(x) は [-∞, ∞] で定義されていましたが、非常に収束の早い関数ですから、グラフを見ても実質上は -4 ~ 4 のあたりに存在する波であると考えることができます。
③ルジャンドル多項式の直交性
ルジャンドル多項式の直交性は、
によって表されます。また [-1, 1] で値をもつ任意の関数はその範囲内で
というように展開でき、その係数 cn は
で与えられます。
ルジャンドル多項式の応用
変数 x を cosx 或いは sinx に置き換えると、-1 ≦ cosx, sinx ≦ 1 ですから、実数全域で定義される使いやすい関数となります。Pn(cosx) のグラフを描いてみると: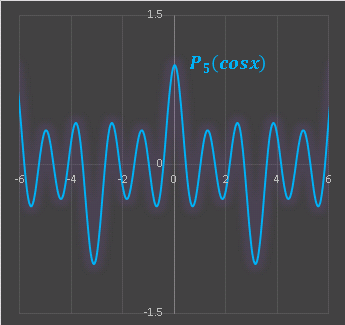
小さな波と大きな波が交互に現れる関数です。電磁気学で多重極展開(電荷の作る電位を求める表式)と呼ばれる手法にはこの形が用いられます。
⇒ ルジャンドル多項式を計算する Function マクロ(ユーザー定義関数)