Excel VBA　数学実験室

【Excelショートカット豆知識】
　[Ctrl] + [PageDown]　次のシートに移動する
　[Ctrl] + [PageUp]　　前のシートに移動する

�@ エルミート多項式　Hermite polynomial

　エルミート多項式 は次のような形で表される多項式です：


　[n/2] はガウス記号で n/2 を超えない整数であることを表しています。エルミート多項式は次のような漸化式を満たします：

　　　　H_{n + 1}(x) = 2xH_n(x) − 2nH_{n − 1}(x)

　具体的に書き表すと、

　　　　H₀(x) = 1
　　　　H₁(x) = 2x
　　　　H₂(x) = 4x² − 2
　　　　H₃(x) = 8x³ − 12x
　　　　・・・・・・・・・

のような形になります。グラフに描くと下のような形になります：

　

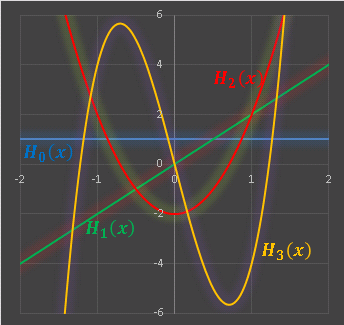
�A エルミート多項式の正規直交化

　エルミート多項式 H_n(x) を正規直交化すると次のような関数になります：


　u_n(x) は−∞ < x < ∞ の範囲で直交する関数です：

　
　δ_mn は m = n のときだけ値 1 をもつという記号（クロネッカーのデルタ）です。 u_n(x) のグラフを描くと次のようになります：

　

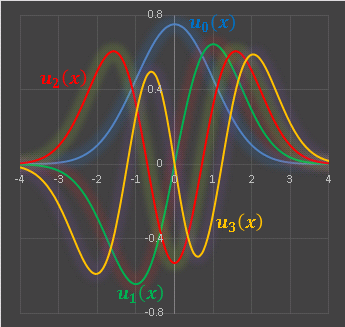
　u_n(x) は量子力学における１次元調和振動子の固有関数として知られています。古典力学の振り子に相当する現象ですが、量子の世界では n によって振動の状態が決定されます。 n の値はエネルギー E_n を定めます。 n が大きいほど E_n が大きく、激しく波打つ関数になります。最もエネルギーの低い u₀(x) は振動しているというよりは、x = 0 近辺にとどまっているという状態ですね。

　u₁(x) で変数 x を x³ に変えてみると・・・・・・

　

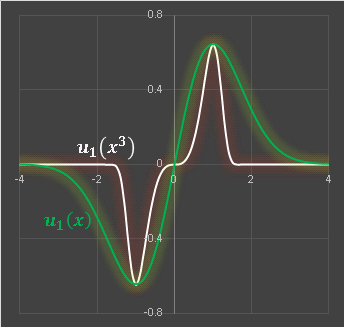
　ピークの幅が狭くなりますが、極大値・極小値は変わりません。同じように変数 xⁿ において n を大きくしていけば、ピークはどんどん鋭くなっていきますが、極値そのものが変化するわけではありません。

　u_n(x) は線形微分方程式の解なので、u_m(x), u_n(x) を適当に選んで重ね合わせてもやはり微分方程式の解となっています。例として u₂(x), u₅(x) を足し合わせてみます：

　

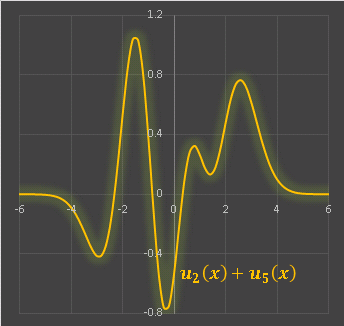
　複雑な関数に見えますが、要は axⁿ + ・・・・・・という形の多項式に exp(−x²/2)を掛けただけの比較的単純な関数です。
　⇒ エルミート多項式を計算する Functionプロシージャ