システムエンジニアが目指す中小企業診断士

　こんにちは！
　EVE2です。

　令和5年の問題を、財務・会計へと進めているのですが、最悪です。時間を十分掛ければ、合格点近くに行きそうなのですが、制限時間60分以内に問題を解こうとすると、最悪な結果になりました。企業経営理論では点数を公開できましたが、財務・会計は、恥ずかしくて、言えません。
　それと、今回、解いた問題は、去年本番で解いた問題なのですが、最初の問題、1分程度で解ける問題でした。去年の本番では、確か、10分ぐらい掛けたような気がするのですが・・・。しかも、間違っていそう・・・。
　まっ、少しは進歩があるようです。
　StudyingのAI実力スコアが合格点を超えていたので、合格したつもりでいたのですが、合格は遠い先で待っているようです。とりあえず、体勢を整えて、合格に向けたがんばりたいと思います。
　では、昨日の続きです。問題を再掲するところから始めましょう！

[経済学・経済政策　平成25度年第15問]


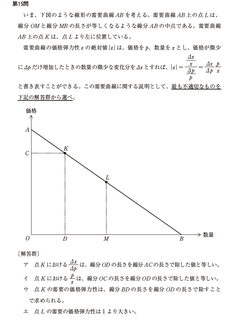
[考え方]
　実は、この問題、正解を判別する方法があります。それは、問題文に、「需要曲線A上の点Lは、線分OMと線分MBの長さが等しくなるような線分ABの中点である」とあります。これは、どの需要曲線もそうだと思うのですが、曲線の中点の価格弾力性は、1となります。つまり、中点の1よりも小さくなれば、価格弾力性は小さくなり、中点よりも大きくなれば、価格弾力性は大きくなるのです。
　ここは、間違いを探すと言うことなので、「エ，点Lの需要の価格弾力性は1より大きい」という解答は明らかに間違っています。
　まっ、この問題は、モデルを単純化した形で出題されているので、一目で分かりましたが、似たような問題でも、違った形で出題されるかもしれません。それを、考えると、この問題を理解するという意味では、もっと深掘りをして見たいと思います。特に、現在、全く解いたことがない過去問を解きながら(去年の過去問は試験後答えあわせしていません)、しみずみとそう感じています。

[設問ア]
　では、設問アから見て行きましょう！
　「点KにおけるΔx÷Δpは、線分ODの長さを線分ACの長さで除した値と等しい」
　
　この設問は、昨日の需要の価格弾力性の調査結果から理解することができます。それは、価格弾力性は、以下の公式で導かれるということを知っていれば、この設問アが合っていることが分かります。

　ε = (ΔQ/Q) / (ΔP/P)

[設問イ]
　では、設問イです。
　「点Kにおけるp÷xは、線分OCの長さを線分ODの長さで除した値と等しい。」

　これは、単純な一次関数です。K点における座標を(a,b)で表現した場合は、点aは、原点からaの長さ(0D)であり、点bは、原点からbの長さ(0C)です。以上から同じ事を言っていることが分かります。

[設問ウ]
　では、次設問ウです。
　「点Kの需要の価格弾力性は、線分BDの長さを線分ODの長さで除すことで求められます。」

　これは、理解できませんでしたので、Bardに手伝ってもらいました。以下が、Bardからの解答です。


[設問エ]
　そして、最後に設問エです。
「エ，点Lの需要の価格弾力性は1より大きい」

　これは、前文で説明した通りです。

[あとがき]
　一目で見てわかる問題だったのですが、深掘りしたことにより、需要曲線と需要の価格弾力性について、より深いレベルで理解できそうです。まだ、ちょっと、設問ウについては、しっくりとしない部分があるのですが、それについては、徐々に理解したいと思います。また、何か訂正するようなことがありましたら、ブログから報告させていただきますので、注目していてください。

　では、また！