図形を反時計回りに回転させる行列
まずは有名な回転行列による演算を再確認していきましょう。この行列は任意の点 (x, y) を原点を中心に 反時計回りに回転させる行列 ですね。具体的に書き表すと、
という演算になります。これを例えば直線の方程式
x = t, y = t
に、θ = pi/6 = 30° とした R30 を作用させると(このブログでは行列右下の添字は回転の角度を表すと決めておきます)・・・・・・

黒い線が元の直線、赤い線が演算後の図形です。このように直線全体が 30°回転します。では Rθ を半径 1 の円の方程式
x = cosθ, y = sinθ
に作用させたらどうなるでしょうか? 「少しも動かないよ。わかりきってるでしょー」と思われるかもしれませんが、一応確認しておきましょう。θ = 20° の R20 で試してみます。
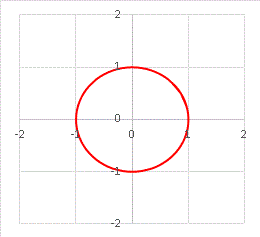
円の形そのままですね。動いた気配はまったくありません。確かに図形自体は動いていないのですが、円周上の各点は 20° 回転しているはずです。それを見るために、元の円をドット(点)で表示すると、回転の様子がわかるはずです:
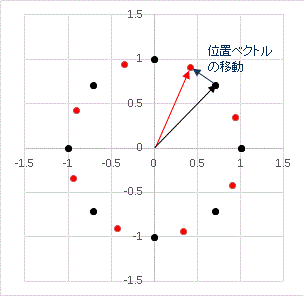
全ての黒い点が赤い点に移り変わっている様子がわかりますね。このように全ての円周上の点が揃って 20° 回転することで、円の形を保持しているのです。