�P�����ɋ߂�������������
�@
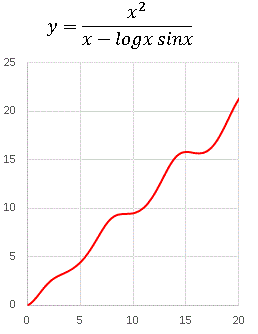
�@�����Ȃ蕡�G�Ȋ��Ɍ����܂����A���̓����J�Ɍ��Ă����܂��傤�B�Q���� y = x 2 �� x �Ŋ���� y = x 2 / x = x �ƂȂ�P�����ƂȂ�܂��B�u������O���I�v�Ǝv���邩������܂��A����̃e�[�}�� �P�����ɋ߂������������� �i�܂� x �� 1 ������� y �����悻 1 ������悤�ȁj���ł��B��̃O���t�����Ă��������B�g�ł��Ă͂��܂����A���� y = x �ɂقډ����悤�ȃO���t�ł��B(5, 5), (10, 10), (15, 15)�̋ߕӂ�ʂ�܂��ˁB����� x 2 �����镪�ꂪ x ��菭���������������ɂ��Ă��邩��ł��B sinx �̕����� +1 ���� �|1 ���������邾���ŕ��ς���� 0 �ł�����A��ǓI�ɂ͑������ɉe�����܂���B���� logx �̕����ł��B���͑O��́u x vs logx �v�������ɂȂ��Ă��܂��B x �� logx ���ׂ����ɁAx �� 0 �̕ӂ�ł� logx ���D���ŁAx ���傫���Ȃ�� x �̂ق��������������Ȃ��Ă����Ƃ������������܂����B��̃O���t�� x ���\���ɑ傫�����ł́i�������Ɋւ��Ắj�P�����̂悤�ɂӂ�܂��ƍl�����܂��B���������͈͂��g�債�Ă݂܂��傤�B
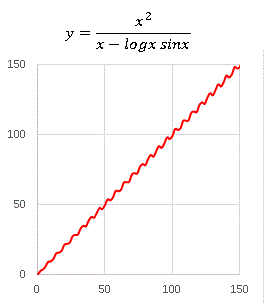
�@�M�U�M�U�̂P�����̂悤�ɂȂ��Ă��܂��ˁB���邢�͂P�����Ɋ��������ւ̂悤�ɂ������܂��B���̊����������ό`���Ă݂܂��傤�B����� logx �ɂ����镔���� sinx + cos(��2x) �Ƃ���ƁE�E�E�E�E�E
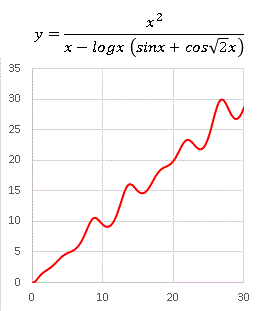
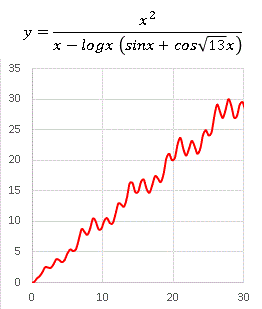
�@���̂悤�ɎO�p���̕ϐ� x �ɂ�����W�����~�����ȊO�̖������ɂ���Ǝ���������܂��B�ȑO�ɂ������悤�Ȃ��Ƃ����܂����ˁB���������������Ă݂܂��傤�B cos(��2x) �� cos(��13x) �ƕό`���܂��B
�@�ƂĂ��s�K���Ɍ����܂����A����ł� (10, 10), (20, 20), (30, 30) �̋߂���ʉ߂��Ă��邱�Ƃɒ��ڂ��Ă��������B�����܂ł� "�P�����I" �ł��邱�Ƃɕς��͂Ȃ��̂ł��B
�@���� y = x 2 �� x �̂P�������܂ސ����Ŋ����ĂP�����I�ȃO���t�ׂĂ݂܂��B�ŏ��� x - sinx �Ŋ����āA 0 < x �̗̈�Ŋ����`���܂��B�u���������ȒP�Ȋ��ɂȂ��Ă��v�Ǝv���邩������܂��A�͂����Ăǂ��ł��傤���B
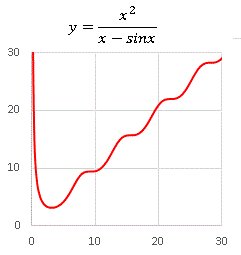
�@3 < x �����肩��͊m���� "�P�����I" �Ȃ̂ł����A���_�t�߂ł͖��炩�ɈقȂ�U�镑�������Ă��܂��ˁB�������͔��ɏ������l�Ŋ����Ă��邱�ƂɋN�����܂��B����������̓I�Ɍv�Z���Ď������Ă݂܂��傤�B x = 0.1 �Ƃ��Ă݂�ƁA
�@���q = 0.1 2 = 0.01
�@���� = 0.1 �| sin(0.1) = 0.1 �| 0.099833417 = 0.000166583
�@���炩�ɂ��̌����� sin �̒l�ɂ���܂��ˁB�������l�ɑ��� sinx �� x �Ƃ����ߎ��������藧���Ƃ͗����n�̕��ɂƂ��Ă͏펯���Ǝv���܂����i���ۂɂ͏������� sinx < x �ƂȂ邱�Ƃ��o���Ă����Ă��������j�A������g���ƁA���� �� x �| x �ƍl���Ă������킯�ł��B�܂茴�_�ɋ߂Â��ƕ���͂ق� 0 �̂悤�Ȍ`�ɂȂ��āi���q�������� 0 �Ɏ������āj�A���̒l���}�������Ă����܂��B
�@����ɍׂ�����͂����݂܂��B��̃O���t�� sinx �� x �����藧�̈�ƂP�����I�ɐU�镑���̈�̊ԂɑJ�ڑт����݂��܂��B����͂Q�����Ƃ��ĐU�镑���̈�ŁA���� �� 1 �̂�����ɂ���͂��ł��B�O���t�ł����ŏ��̒J�ɋ߂��Ƃ���ł��ˁB���̒��S�_��������ɂ� x �| sinx = 1 �Ƃ����������𐔒l�I�ɉ����Ă݂�����̂ł��B y = x �| sinx �|1 �̃O���t��`���āAx ���ƌ����_��T���܂��B���x�����߂邽�߂ɂ� x �̍��ݕ���x ���ł��邾������������K�v������܂��B�����ł͇�x = 0.001 �Ƃ������x�ʼn������߂Ă݂܂��B��̑O�́A���������ȒP�Ȃ��Ƃ����ɂ����������v���O�����������K�v������܂����B Excel �͖{���ɕ֗��ł��B
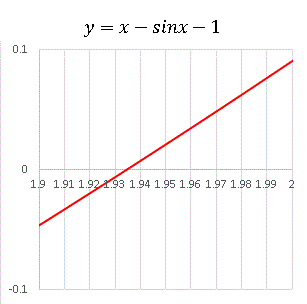
�@��}�� y = x �| sinx �|1 �� x = 1.9 �t�߂��g�債���O���t�ł��B�������� y = 0 �ƂȂ�_�� x = 1.935 �Ƌ��߂邱�Ƃ��ł��܂��B�o�͂��ꂽ���l�f�[�^�J�Ɍ���� x = 1.936 �Ƃ�������ɍ������x�̉����܂��B���̓_�𒆐S�Ƃ��Ă��������͈͂łQ�����̂悤�ɐU�镑���킯�ł��B
�@
Excel 2013 ���y��������@
�@�O������ʂ�AExcel 2013 ���y��������@�ł��B����̑�����s���Ό��I�ɉ��P����͂��ł��B�ȉ��� Windows 7 �ł̎菇�ł��̂ŁAOS �ɂ���Ď�̈Ⴂ������Ƃ͎v���܂����A���̂ւ�͓K���ɒ������Ă��������B1. �u�X�^�[�g�v�{�^�����N���b�N���܂��B
2. �E���̃v���O�����ƃt�@�C���̌����Ə����ꂽ�{�b�N�X�� regedit �Ɠ��͂��Č����A�C�R�����N���b�N���܂��B
3. ���W�X�g���G�f�B�^�̋N���A�C�R�����\�������̂ŃN���b�N���܂��B
4. �����̉�ʂ��X�N���[������� "HKEY_CURRENT_USER" �Ƃ����t�H���_������͂��Ȃ̂ŁA������J���܂��B
5. ���̒����� "Office" �Ƃ������ڂ�����͂��Ȃ̂ŁA�T���ĊJ���܂��B
6. ����� "15.0" �� "Common" �� "Graphics" �Ə��ɊJ���ƉE���̉�ʂ� "DisableAnimations" �Ƃ������ڂ�����Ǝv���܂��B����������ƍŏ��͂Ȃ�������������܂���B�����Ȃ���ΉE���̉�ʂʼnE�N���b�N���� DWORD �l��V�����lj����Ė��O�� "DisableAnimations" �Ƃ��Ă��������B
7. "DisableAnimations" ���E�N���b�N���āu�C���v��I�����A�l�̃f�[�^�� "1" �Ɠ��͂��܂��B
8. Excel ���N�����Ă݂Ă��������B���̕ςȏd������������Ă���͂��ł��B
�@�܂��Ƃ������AExcel 2013 �͂��̂悤�ɐݒ�ύX�����Ȃ��Ǝg�����ɂȂ�Ȃ����炢�d���ł��B�y���Ȃ�����v������ Excel �Ő��w�ł��܂��B�F��������Ў����ŐF�X�ȃO���t��`���Ă݂Ă��������B
�m�[�x�������w�܂ł��I
�@���{�l���܂������w�Ńm�[�x���܂��Ƃ�܂����ˁI�@���{�̊�b�����̐����̍������ؖ����ꂽ���Ƃ͖{���Ɋ������ł��B�����w�ł͂ǂ̕���ɂ����_�Ǝ���������܂��B�����œ���ꂽ�f�[�^�ŗ��_��g�ݗ��Ă��A�g�ݗ��Ă�ꂽ���_�̗\�z���܂������Ŋm�F����Ƃ����J��Ԃ��ŕ����w�͐i�����܂��B�����܂��ꂽ���c����͑f���q�����w�̎����ɐ^���Ɏ��g��ł����l�ł��B�����Č��o�����j���[�g���m�����_�ŗ\�z�����l�������Ȃ��Ƃ����ϑ��f�[�^�����Ƃ��A�j���[�g���m�U���Ƃ����唭���ɂȂ������̂��ƌ���Ă����܂����B�@���_�̗\���ƈ�v���Ă����Ƃ������A�قȂ��Ă����Ƃ��̂ق����w��̐��E�͊��C�Â��܂��B���_����������l�͗��_���C��������A�V�������_��g�ݗ��Ă�Ƃ�����d���ɒ���ł��邩��ł��B
�@���͊w������ɗ��_�����w���w��ł��܂����̂ŁA��͂薈�N�A�N�������w�܂���܂���̂��낤���ƋC�ɂȂ��Ă��܂��܂��ˁB������j���[�X�����āu���[�A������[�I�v�Ǝv�킸������グ�Ċ��ł��܂��܂����B
�@���̃u���O��ǂ�ł��������Ă���ǎ҂̊F����������n�̐l���唼���Ǝv���܂��B�����n�̂ǂ̕���ɐi�ނɂ��Ă��i���邢�͌o�ϊw�̂悤�ȕ���ł����Ă��j�A���w�͎v�l�̍�����z����Ȋw��ł��B�������ނ����ɖ������������łȂ��A��������Č��̗͂��āA�u���[��B���͉��������ǁA���̃O���t�̍\���͂ǂ��Ȃ��Ă���̂��낤�H�v�ƁA����������p�x���琔�w�߂Ă݂Ă��������B��������ƍ��܂Ō����Ȃ������i�F�������Ă����肵�܂��B
�@ �@