階差 √n の数列
次のように階差 √n で定義される数列を考えます。
一見して簡単そうに見えますが、Σ√n を簡単に表すことができないので、階差数列の公式を使っても一般項を求めることができません。というわけでエクセルに頼りましょう。
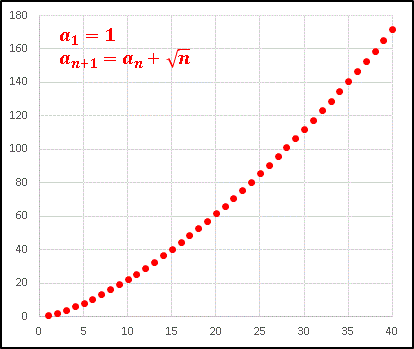
n が小さいうちは緩やかなカーブの上に乗っていますが、n が大きくなってくるとほぼ直線的に並びます。次は
という数列です。各項に加えられる数字はかなり小さくなります。
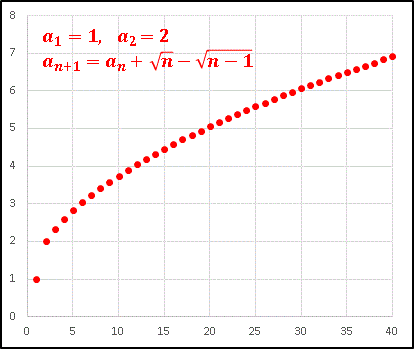
ほぼ予想通り n が大きくなるほど値の増加率が落ちてゆく数列ですね。
次は三角関数を組込んで、
という数列をプロットしてみましょう。
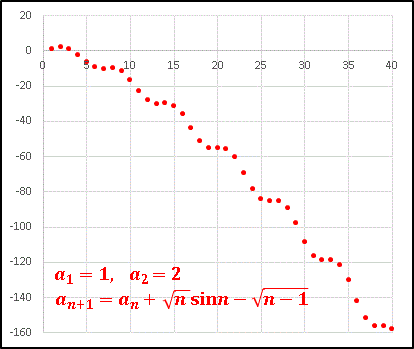
...... かなり変わったグラフになりましたね。エクセルではこうした複雑な漸化式も簡単に扱えるので。皆さんも色々試して面白いものが見つかったらぜひ教えてください。